长江防洪实体模型垂线流速相似性研究

孙贵洲，卢金友，赵根生

（1.长江科学院河流研究所，武汉 430010；2.荷兰代尔夫特科技大学水利工程系，荷兰；3.河海大学水利水电工程学院，南京 210098）

长江防洪实体模型垂线流速相似性研究

孙贵洲1，卢金友1，赵根生2，3

（1.长江科学院河流研究所，武汉 430010；2.荷兰代尔夫特科技大学水利工程系，荷兰；3.河海大学水利水电工程学院，南京 210098）

根据实测资料，采用3点法、5点法对比计算分析了原型和长江防洪实体模型的垂线平均流速两者间差异，同时比较分析原型与模型流速沿水深分布偏离程度。采用明渠对数流速公式探讨了模型变态后流速沿垂线分布的规律，在此基础上提出了长江防洪实体模型垂线平均流速与相对水深某位置处点流速的关系，观测资料分析表明，模型相对水深为0.6处的点水深处流速与垂线平均流速基本一致。

长江防洪实体模型；变态；垂线平均流速；相似性；3点法；5点法

1 概 述

实体模型变态后，对于三维水流而言，惯性力粘滞力比、惯性力重力比、压力惯性力比均会发生偏离［1］。变态河工模型在惯性力重力比相似方面，一般按α2u／（αgαh）＝1设计及控制模型的边界条件，而满足铅垂方向相似准则的比例关系式（α2uαh）／（αgα2l）＝1得不到遵守。因此，变态模型惯性力重力比的不相似将主要表现为垂直方向的不相似，从而使得垂直方向水力要素的相似性受到影响［2－5］。长江防洪实体模型［1］主要研究平面二度流问题，只要遵循惯性力重力比α2u／（αgαh）＝1相似条件，并能保证河底及河岸各部分阻力相似，水面线及垂线平均流速沿河宽分布的相似是可以得到保证的。

基于上述相似理论，长江防洪实体模型开展了原型荆江河道水流特性等有关问题研究，模型布置密集断面观测不同流量下河道流速流向变化。由于模型变态后流速沿水深分布规律与原型将产生一定偏离，断面点平均流速取值采用何种测量方式尚需检验论证。本文根据原型和模型实测流速资料对比分析3点法、5点法应用于原型和模型计算求得垂线平均流速值精度差异，同时比较分析原型与模型断面点流速沿水深分布偏离程度。此外，采用明渠对数流速公式探讨了长江防洪实体流速沿垂线分布与原型不同的规律，在此基础上提出本模型垂线平均流速与相对水深某位置处点流速关系，以期在满足测量精度下采用较少测点流速代表垂线平均流速方法，提高模型试验观测效率。

2 用3点法与5点法实测流速比较

2.1 原 型

天然河道垂线流速测量按照水文测量有关的规程规范，以水深为标准，选择1点法、3点法或5点法进行测量，然后采用加权平均的方法计算断面各垂线的平均流速。

选取荆江河段分汊段、顺直段和弯曲段的典型断面关9和荆18，董5和荆14，以及荆28和荆50，根据原型实测垂线3点及5点流速，加权分别求得垂线平均流速沿河宽分布如图1至图3所示。

图1 分汊段典型断面流速分布Fig.1 Velocity distributions in the representative cross-sections of braided reaches

图2 顺直段典型断面流速分布Fig.2 Velocity distributions in representative cross-sections of straight reaches

图3 弯曲段典型断面流速分布Fig.3 Velocity distributions in the representative cross-section of curved reaches

3种河型典型断面分别采用3点法和5点法计算的断面垂线平均流速沿河宽分布基本吻合，仅在部分测线位置出现了5点法和3点法计算的流速值不一致的现象，地形变化比较平缓的断面，2种测量方法的测量误差较小，地形急剧变化的断面则相对误差较大。6个断面每根垂线上2种测量方法计算的垂线平均流速的最大误差、最小误差和平均误差如表1所示，其中，流速最大相对误差为2.40%，均在允许的精度范围内。

2.2 长江防洪实体模型

选取长江防洪模型典型断面荆26、荆66、荆78，按3点法和5点法观测并计算断面垂线平均流速。由图4可知，5点法测流计算的结果一般会比3点法测流的结果偏大，这种现象在断面的深槽和地形变化比较复杂的部位尤其突出。两种测量方法的最大相对误差为2.7%，平均误差为1.8%，偏差值较原型略大。

表1 原型3点法与5点法垂线平均流速误差Table 1 Deviations of the vertical average velocity measured by 3-pointmethod and 5-pointmethod in prototype

图4 典型断面流速分布Fig.4 Velocity distributions in representative cross-sections

3 模型变态后垂线流速分布与原型相似性分析

如前所述，河工模型变态后，断面垂直方向流速分布与原型有偏离，垂线平均流速相似则可以得到保证。采用荆江河段原型和模型典型断面的垂线流速分布实测资料，分析荆江原型与模型垂线流速分布规律，得出断面垂线平均流速与其对应的相对水深关系，并与实测资料相互验证。

3.1 模型与原型垂线流速分布

为了达到模型与原型垂线流速分布可比性，选取了原型与模型地形较为相似、垂线平均流速比较接近、垂线水深基本一致的断面，对模型和原型垂线流速分布进行对比分析。典型断面垂线实测流速分布如图5所示。

图5 原型与模型典型断面垂线流速分布对比Fig.5 Comparisons of vertical velocity distributions in representative cross-sections between prototype and model

模型变态后（长江防洪模型变率为4），断面点流速沿垂线的分布规律与原型存在较大的差异，模型垂线底部流速较原型小，随着相对水深递减，对应流速与原型差值亦将缩小，并于相对水深0.6附近的某个位置与原型流速相等；当模型垂线流速超过该临界位置后，模型流速则大于原型流速，且差值随相对水深减小而增大，该趋势直至水面位置。

为了进一步分析模型与原型垂线点流速分布规律的差异，采用了误差和统计分析的方法对以上各个典型断面垂线流速分布的试验数据与原型实测数据进行了对比分析，其分析结果如图6所示。

从模型与原型垂线点流速差异的概率分布可以看出，模型的垂线点流速与原型较接近的位置在0.6H附近；在0.6H以下的模型垂线点流速小于原型垂线点流速；在0.6H以上的模型垂线点流速则大于原型垂线点流速。

图6 不同水深下变态模型与原型垂线点流速变化Fig.6 Variation of vertical velocities in different water depths of distorted model and prototype

3.2 模型与原型垂线流速分布相似性分析

在明渠水流运动中，其均匀流阻力系数满足爱因斯坦［6，7］建立的关系式如下：

式中：λ为阻力系数；R为水力半径；χ为校正系数；κs为明渠水流周界上的粗糙突起高度。

对于明渠宽浅断面又满足如下关系：

式中H为水深。

由式（1）和式（2）可以得到

故模型的阻力系数比尺可以表示如下：

式中：脚标m为模型值；脚标p原型值。

将式（4）变换如下：又因为长江防洪实体模型［1］存在，则

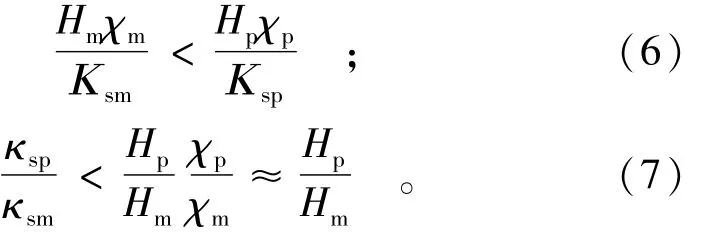
故ακs＜αh。

将式（5）进一步改写如下：

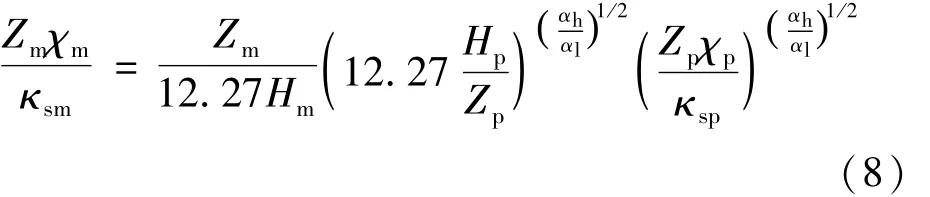
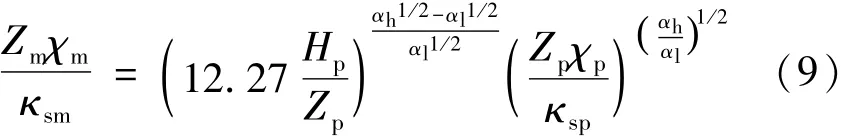
在明渠水流运动中，垂线流速分布可以采用爱因斯坦根据坎鲁根资料修正的适用于紊流各区的公式：

式中，u为垂线点流速；U为摩阻流速，U＝；H为水深；Z为垂线上某点高程下的水深；κs为明渠水流周界上的突起高度；J为水面坡降。

原型和模型的垂线流速分布规律均遵守式（10），可表示如下：

对于变态模型，摩阻流速存在如下比尺关系

式中：αu为摩阻流速比尺；αh为垂直比尺；αl为水平比尺。

将式（9）和式（5）代入式（11）得

进一步改写式（15）得

式中αv，αu分别为垂线平均流速比尺、垂线点流速比尺。

利用式（10）沿水深积分，可以得到垂线平均流速

上式说明采用式（10）形式的垂线流速分布公式，无论原型和模型，0.632H处的点流速和垂线平均流速一致，并与实测资料基本吻合。

为分析本模型垂线流速分布规律，根据模型设计比尺，按照式（16），分别点绘原型水深3 m，10 m水深下相对水深与αu／αv关系，见图7。

图7 原型不同水深下模型断面垂线αu／αv与相对水深关系变化曲线Fig.7 αu／αvversus relative water depth in the condition of different water depths in prototype

当η＝4，（H－Z）／H＜0.6，αu＜αv，表明本模型垂线流速偏大，偏离度随水深增大而增大，一般在8%以内；当（H－Z）／H＞0.6，模型的流速偏小，偏离度随水深减小而增大，Z＝0.2H水深处偏离度约30%。模型与原型垂线流速分布规律与实测资料分析结果基本一致。

4 模型3点法和1点法垂线平均流速误差分析

假定模型测流的5点法平均流速可近似代表垂线平均流速，3点法和1点法测流的结果如表2所示，在3 9000 m3／s和19 600 m3／s下，各典型断面中，3点法测流的最大误差为3.50%，1点法测流的最大误差为5.66%。由此可见，长江防洪模型上荆江模型断面垂线平均流速可采用3点法进行测量，在断面地形较平缓处亦可采用相对水深0.6处附近测点流速代表，两者的误差均在精度允许的范围内。

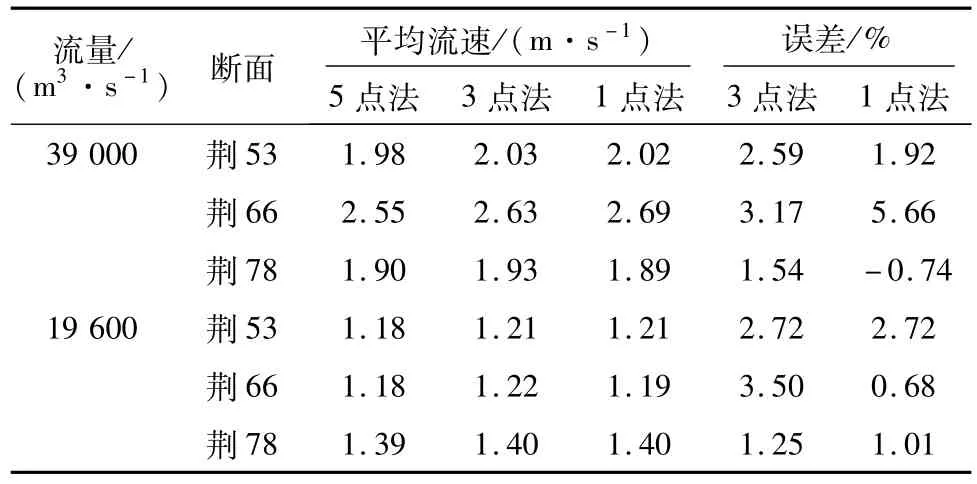
表2 模型3点法与1点法垂线平均流速误差Table 2 Deviations of the vertical average velocity measured by 3-pointmethod and 1-pointmethod in model

5 结 语

采用荆江原型与长江防洪实体模型断面垂线流速实测资料，分析不同方法计算垂线平均流速差异性，并对变态模型与原型垂线流速分布规律进行了探讨，得到以下主要初步结论：

（1）采用3点法及5点法计算荆江原型和模型断面垂线平均流速时，无论河型、水深各异，两者之间差值都较小，相对误差均在3%以内，表明荆江原型及模型断面垂线平均流速采用3点法测量即可满足精度要求。

（2）经实测资料的统计分析，模型与原型垂线点流速值相等的位置在相对水深大致为0.6的附近；按照对数流速分布公式推导出原型与变态模型垂线平均流速值与相对水深0.632处点流速相等。

（3）根据长江防洪模型设计（η＝4），当（HZ）／H＜0.6时，αu＜αv，即模型流速较原型大，偏离度随水深增大而增大；当（H－Z）／H＞0.6时，αu＞αv，即模型流速较原型小，偏离度随水深减小而增大。原型与变态模型垂线流速分布规律与实测资料分析结果基本一致。

（4）根据以上初步研究成果，长江防洪实体模型垂线平均流速可采用3点法测量，在断面地形较平缓处亦可取相对水深0.6处流速值。

［1］ 长江科学院.长江防洪模型设计说明［R］.武汉：长江科学院，2002.（Yangtze River Scientific Research Insti-tute.Introduction of design for the Yangtze River flood controlmodel［R］.Wuhan：Yangtze River Scientific Re-search Institute，2002.（in Chinese））

［2］ 胡艳芬，余明辉，吴卫民.变态对河工模型中弯道水流相似性的影响［J］.水科学进展，2008，18（1）：63－67.（HU Yan-fen，YU Ming-hui，WU Wei-min.Effect of the distortion ratio on flow similarity in the physicalmodel［J］.Advances in Water Science，2008，18（1）：63－67.（in Chinese））

［3］ 虞邦义.河工模型相似理论和自动测控技术的研究及其应用［D］.南京：河海大学，2003.（YU Bang-yi.Riv-ermodel similarity theory and automaticmeasurementand control technology and its research and application［D］.Nanjing：Hohai University，2003.（in Chinese））

［4］ 姚文艺.黄河河道实体模拟若干设计理论及其应用［D］.南京：河海大学，2005.（YAO Wen-yi.Series of design theories and applications on the physical simulation of the Yellow River［D］.Nanjing：Hohai University，2005.（in Chinese））

［5］ 张红武.黄河下游洪水模型相似律的研究［D］.北京：清华大学，1995.（ZHANG Hong-wu.Study on the flood model similarity of the lower Yellow River［D］.Beijing：Tsinghua University，1995.（in Chinese））

［6］ 徐正凡.水力学［M］.北京：高等教育出版社，1987.（XU Zheng-fan.Hydraulics［M］.Beijing：Higher Edu-cation Press，1987.（in Chinese））

［7］ 张瑞瑾.河流泥沙运动力学［M］.北京：水利电力出版社，1989.（ZhANG Rui-jin.Mechanics of River Sedi-ments［M］.Beijing：Hydraulics and Hydropower Press，1989.（in Chinese））

［8］ 长江科学院.长江荆江河段近期河道演变分析报告［R］.武汉：长江科学院，2006.（Yangtze River Scien-tific Research Institute.Analysis report on the river evo-lution of Jinjiang Reaches of Yangtze River in recentyears［R］.Wuhan：Yangtze River Scientific Research Institu-te，2006.（in Chinese））

［9］ 王学功.三维变态河工模型可行性分析［J］.安徽水利水电职业技术学院学报，2002，2（1）：6－9.（WANG Xue-gong.Feasibility analysis of 3-D river distorted scale model［J］.Journal of Anhui Technical College of Water Resources and Hydroelectric Power，2002，2（1）：6－9.（in Chinese））

［10］韩海骞.变态河工模型中的水流阻力相似分析［J］.浙江水利科技，2005，（6）：3－4.（HAN Hai-qian.Similar analysis of flow resistance in distorted river model［J］.Zhejiang Hydrotechnics，2005，（6）：3－4.（in Chi-nese））［11］张红武，江恩惠、白永梅，等.黄河高含沙洪水模型的相似律［M］.郑州：河南科学技术出版社，1994.（ZHANG Hong-wu，JIANG En-hui，BAIYon-mei，et al.Similarity Law of Hyper-concentrated Flood Model for Yellow River［M］.Zhengzhou：Henan Science and Tech-nology Press，1994.（in Chinese））

［12］李旺生.变态河工模型垂线流速分布不相似问题的初步研究［J］.水道港口，2001，22（3）：113－117.（LI Wang-sheng.Preliminary study on vertical velocity distri-bution of distorted river model［J］.Journal of Waterway and Harbor，2001，22（3）：113－117.（in Chinese））

［13］郑国栋，郑邦民黄本胜，等.变态模型水流相似的精度及误差分析［J］.水动力学研究与进展（A辑），2005，20（1）：33－37.（ZHENG Guo-dong，ZHENG Bang-min，HUANG Ben-sheng，et al.Analysis of flow similarity accuracy and error in distorted model［J］.Journal of Hydrodynamics（Ser.A），2005，20（1）：33－37.（in Chinese））

（编辑：曾小汉）

Study on Sim ilarity for Profile Vertical Velocities in Cross-sections of Yangtze River Flood-control Physical M odel

SUN Gui-zhou1，LU Jin-you1，ZHAO Gen-sheng2，3
（1.Yangtze River Scientific Research Institute，Wuhan 430010，China；2.Department of Hydraulic Engineering，Delft University of Technology，the Netherlands；3.College ofWater Conservancy and Hydropower Engineering，Hohai University，Nanjing 210098，China）

According to the comparative analysis of the differences between data measured by three-pointmethod and five-pointmethod used in the Yangtze River Flood Control prototype and model，and those data measured by vertically-average flow velocitymethod adopted in the physicalmodel，the deviation degrees of prototype-model flow velocities alongwater depth are compared.The authors discuss the law of velocity distribution along the vertical di-rection aftermodelmetamorphosis using the Nullah-Logarithmic velocity equation，and，on the basis of this analy-sis，propose the relations between the average vertical velocity and the relative location of the depth.Observation data analysis show that velocity of the 0.6 relativewater depth is basically consistentwith the average vertical veloc-ity.

Yangtze River Flood-control Physical Model；distortion；profile of vertical velocity；similarity；three-pointmethod；five-pointmethod

TV149.2

A

1001－5485（2010）03－0012－05

2009-03-17

孙贵洲（1968-），男，湖北广水人，高级工程师，主要从事河流泥沙专业研究，（电话）027-82829870（电子信箱）sungz888＠163.com。