金融脆弱性研究中的多重均衡模型*
陆家骝,陆 婷
金融脆弱性研究中的多重均衡模型*
陆家骝,陆 婷
多重均衡模型是论证金融体系脆弱性的一个重要技术方法。这个方法的思想性在于颠覆了市场均衡惟一性和最优性的主流经济学教条,从而可以解释金融产业或金融市场在现实中的系统性波动和危机的发生。文章通过两个代表性多重均衡模型的考察,分别从内因和外因的层面表明,市场体系的内在动力会自发地导致金融市场进入均衡的多重结果,金融市场体系因此是脆弱的。政府的行为如果能够满足某些约束条件,其福利改进的功能就是不言而喻的。
多重均衡;金融脆弱性;次优均衡
2008年以来,由世界主要的资本主义经济体引发的全球性经济危机导致学术界对于主流经济学的一些传统教条进行反思。这些反思主要聚焦于两个基本问题。第一个问题同西方国家过去二三十年间极力推动的经济全球化过程相关,即放任市场力量,实行自由贸易和自由投资政策,世界最终会是一个平衡发展的、各国都能发挥其竞争优势的国际经济分工体系呢,还是会产生一个贸易和经济结构全面失衡的非稳定世界?在这次危机之前,主流的观点是前者,而现在,学术界正在考虑后一种可能性的学理基础。第二个问题在逻辑上同第一个问题一致,但在西方学者看来,它比第一个问题更重要。这个问题就是,如果放任市场力量会导致一个各国都能发挥其竞争优势的国际经济分工体系,那么在这个分工体系高端的西方国家自由经济的稳定性又是如何的呢?在这次危机之前,学术界主流的观点是市场原教旨主义的,认为包括金融产业在内的知识型经济在市场力量的作用下是自然而然稳定的,其均衡有着内在的惟一性和最优性。因此,在这个高端主导下的世界经济过程也具有内在的稳定性。然而现在,主流经济学的观点似乎不如以前那般自信了,市场力量会导致多重均衡而非惟一均衡,次优世界而非最优世界的研究再次为人们所重视。
以这次全球危机源头的产业为对象,本文在这里考察金融产业或金融市场体系脆弱性研究中的一种主要技术方法——“多重均衡模型”方法。作为国家社会科学基金重点项目研究的一个内容,我们还将在另外的文章中讨论金融脆弱性研究的其他逻辑方法①如伯南克和戈特勒(Bernanke and Gertler),米什金(Mishkin)等学者的“不对称信息模型”;凯恩斯、明斯基等人的金融体系非稳定假说等。。
一、金融机制协调失败的多重均衡模型
金融体系内生机制协调失败的多重均衡模型发端于戴芒德和戴比威格(Diamond and Dybvig)于1983年发表的一篇论文。在文中他们推出一个令当时学人吃惊的金融脆弱性证明,其中金融脆弱性是金融市场的内在属性。他们选择“银行挤兑”这一危机发生情况下通常出现的现象作为研究对象,建构起一个“银行挤兑”的均衡模型。这个模型显示,因为人们需要在随意的不同时间点上进行消费,银行发行活期存款的行为会使得人群更好地进行风险分担从而增进一个竞争性市场的福利。然而,活期存款合同在提供这种福利增进的同时,也会产生一种我们所不希望的均衡,即在担心银行有可能倒闭的情况下,所有存款者的恐慌性挤兑,包括那些在一般情况下会继续持有活期存款的存款者。所以,作为一种内在的均衡状态,银行经营当中的恐慌现象是自然而然发生的,并不需要什么特别的原因。
为了说明危机是预期自我实现的结果,戴芒德和戴比威格设计了一个三期的(T=0,1,2),只包含一种均质商品的简单模型。通过没有风险的生产活动,他们将各种资产的非流动性引入了模型。生产的情况是这样的,如果只运营一期,那么每单位的投入只产生1单位的产品;如果运营二期,则会产出更高单位的产品R>1。因此,生产过程可以表示为:
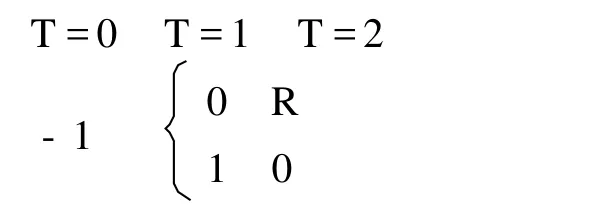
其中对于(0,R)和(1,0)的选择必须在T=1时完成。
在T=0时,消费者都是相同的,所有的消费都只在T=1或T=2时发生。存在这样两类消费者,一类是只看重时期1消费的“超前消费者”,另一类是只看重时期2消费的“后滞消费者”。他们从时期1开始明白各自所属的消费者类型。此外,所有的消费者都可以在无须成本的情况下私储商品而且不为别人所知道。没有人会在时期0与时期1之间储存商品,因为生产过程可以提供至少相同的消费商品;当然,如果是储存到时期2,生产过程就会提供比较多一些的消费商品。假如一个后滞消费者在时期1得到了消费商品,他会储存这些商品直到时期2才消费。令cT表示某消费者在时期T得到的商品,人们可以观察到的一个后滞消费者在T=2的消费就可表示为他自T=1时的储存加上他在T=2时的所得,即c1+c2。这样,就人们可公开观察到的变量cT而言,每一位消费决策者j都有一个包含给定状况下私有信息的状况依赖的效用函数。假定这种效用函数的形式是:

其中1≥ρ≥R-1且效用函数u:R++→R是二次连续可微,严格凹的增函数,满足Inada条件u′(0)=∞和u′(∞)=0。消费者的决策问题因此就是在既有信息的条件下最大化他们的预期效用,E[u(c1,c2:θ)]。
消费决策者连续集合的一个部分t(0,1)为超前消费者,并且以t为条件,每个决策者都同等自由地、独立地决定是否成为超前消费者。可以视t的值为一个常数,每一个消费者在时期0拥有一单位的商品而在其他时期不拥有商品,活期存款合同使得每个消费决策者能够用时期0的1单位储蓄在时期1取出r1单位的固定收益。只要没有出现资产的挤兑现象,银行的承兑业务就会在时序中随机地、正常地进行。应当注意,活期存款合同业务是满足时序约束的。合同具体规定银行对任何个体的支付只取决于该个体在既有时序中的位置,而不是其以后在时序中位置的信息。可以设想银行为借贷双方共同拥有并且在时期2清盘,于是在时期1没有提兑的消费决策者就在时期2拥有该银行资产的部分股权。令V1为在时期1提取一个单位的活期存款所得的收益,它取决于存款者在时期1时的时序位置。令V2为在时期2提取一个单位的活期存款所得的收益,它取决于存款者在时期1时提出存款的总额。将它们用公式表示如下:

其中fj是在存款者j之前银行已被提款的数量,而f则是活期存款提款的总额。两者都是以总活期存款额的分数来计量的。令wj为存款者j打算在时期1提取的他的存款额的分数,这样一个超前消费者从每单位存款的存款收益中获得的消费就是wjV1(fj,r1)。而一个滞后消费者从每单位存款的存款收益中获得的全部消费就是wjV1(fj,r1)+(1-wj)V2(f,r1)。
可以看到,活期存款合同能够使得充分信息条件下的最优风险分担成为一种均衡状态。设r1等于充分信息条件下超前消费者的最优消费,且存款合同恰好符合时序位置,那么超前消费者在时期1提款而滞后消费者等待就是一种均衡状态。当然,如果这一切都符合预期。消费商品的这种均衡达成的是最优风险分担。为了更清楚地说明这一点,令表示超前消费者在时期k的消费表示滞后消费者在时期k的消费,于是最优消费应满足以下限制条件:

方程式(3)表明能够延期消费的人会延期消费;方程式(4)表明消费者的边际效用是同生产的边际生产率相一致的;而方程式(5)是资源约束。依据假设,ρR>1并且相对风险厌恶值总是大于1,方程组(3)至(5)因此意味着最优消费水平满足条件将f=t和代入方程式(1)和(2),我们看到V1(fj,r′1)=依据方程式(4),我们可以从ρR>1导出所以,当超前消费者需要在时期1提出存款消费时,所有滞后消费者宁愿等到时期2消费。这表明f=t是一个均衡。
同样也会存在着另一种均衡状态,这就是银行挤兑均衡。所有的人都陷入恐慌,急着要将自己的存款在T=1时提出。假如危机只是预期的状况,那么所有的存款决策者都会考虑在时期1提出存款,因为存款的面值要比银行资产的清算价值高。这就是非流动索取权向流动索取权的转换,它既是银行提供流动性服务的要求,也是人们怀疑银行会出现挤兑现象的原因。对于所有r1>1的情况,出现银行挤兑都是一种均衡状态。但是如果r1=1,则因为0≤fj≤f只能产生V1(fj,1) 需要注意的是,以上模型并没有引入货币或风险机制,然而银行挤兑问题却是在模型中自发形成,即在对于流动性偏好或资产回报没有任何外在冲击的情况下银行挤兑照样发生。然而,这个模型还是有一个缺点,就是它缺乏预测能力。模型假设银行经营中的恐慌现象是自然而然的事情,取决于存款者的信心状况,也就是取决于滞后消费者是否提前提款。如果几乎所有的存款者都决定在时期1提款,那么提前提款对于每一位存款者来说就都是明智的选择。反之,如果滞后消费者都打算到时期2才提款,则延期兑现对于每一位滞后消费者来说就都是明智的选择。于是,银行体系的经营失败实际上就是一种系统内协调机制失败(coordination failure)。 为摆脱这类协调机制失败,阿伦和盖尔(Allen and Gale)于2000年发表论文对非实质性银行挤兑与实质性银行挤兑加以区别。若银行本身具有充分的资源来兑现对于超前消费者在时期1提款的承诺同时又能对于滞后消费者提供相等或更多的收益支付,即银行能够满足其激励与约束的限制条件,那么,那些产生于自我实现预期的恐慌性挤兑就都是非实质性的了。反之,若银行不能够同时满足其约束和激励的限制条件,则实质性银行挤兑就会发生。同时,作为对于协调机制失败模型的改进,阿伦和盖尔还将生产过程改变为两类投资过程:短期投资和长期投资,并且允许银行在时期1能够进入一个资产市场。短期投资在1期之后人均产生1个单位的回报,而长期投资则须两期才有收益。于是在流动性与收益之间就有一个权衡,因为长期投资会有较高的回报R>1。存在这样的一个资产市场,而不是对长期投资的物质结果清盘,这为银行提供了另外一个流动性的来源。 以η表示成为一个超前消费者的概率,以cT表示在时期T=1,2时的消费,这样一个消费决策者事前的效用就是: 时点效用函数u:R++→R的相关假设同前面模型的假设一样。阿伦和盖尔在模型中识别了“内在不确定性”的三个原因,所谓“内在不确定性”是指这些不确定性起源于系统本身的基本要素的随机波动。第一个原因是每一个消费决策者都面临着自己是提前消费还是延后消费的个体偏好的不确定性。第二个原因是每一家银行都面临着存户中有多少数量是超前消费者的个体不确定性。第三个原因是经济中存在着超前消费者比例的总体不确定性。具体来说,总体不确定性可以表示为一种总体状况δ,它是一个在区间[δ0,δ1]上有连续的,正的密度函数f(δ)的随机变量,并且δ0<δ1为有限数。银行的个体不确定性可以表示为一个有着累积分布函数G(α)的随机变量α。在状况(α,δ)的情况下某一银行中的存户成为一个超前消费者的概率可以表示为η(α,δ),其中 且ε≥0是一个常数。运用传统的大数定理,在状况(α,δ)的情况下某一银行中的存户成为一个超前消费者的分数或比例等于其概率η(α,δ)。而在整个经济中随机变量α的平均值可以假设为一个常数,等于因此,仅当ε>0时,经济中才会存在总体的内在不确定性。 一家银行在短期资产上人均投资y单位而在长期资产上人均投资(1-y)单位。同时它也向消费者提供活期存款合同,合同允许消费决策者或者在时期1取出d单位消费,或者等到时期2分享银行资产价值。显而易见,存款合同激励相容的充分必要条件是滞后消费者在时期2分到的价值至少要等于d。如果用p(δ)表示在时期1状况δ下一单位未来消费的现时价格,则该银行在时期1的资产价值就是y+p(δ)R(1-y)。这样,激励相容同银行预算约束相一致的条件就是: 只要这个激励相容的条件得到满足,滞后消费者就会等到时期2才提款。但如果这个约束条件不能满足,则显然有: 要是所有的消费决策者都在时期1提款,这家银行就会倒闭。在破产的情况下,银行有义务清算其资产并平等地分配,每个消费者得到的价值为y+p(δ)R(1-y)。 令xT(d,y,α,δ)表示状况为(α,δ)并且银行选择(d,y)的情况下个体在时期T的消费,又令x=(x1,x2),于是银行的决策问题可以写成: 在给定价格函数p(·)的情况下,如果有序数对(d,y)是决策问题(10)的解,它就是最优的。可以用一个整数m<∞和一个数列ρ=(ρ1,…,ρm)来定义时期0消费者的一个单位分割,其中ρi≥0并且消费者分成m组,每组包含消费者的一个侧度ρi。那些同组的消费者有关的银行会向他们提供活期存款合同di和投资组合yi,两者都以人均计量。资源的一个配置就是由一个单位分割(m,ρ)和一个数对排列(d,y)=所构成,其中对于m=1,…,m,有di≥0,0≤yi≤1。 对于任何一个总体状况δ,如果一个资源配置(m,ρ,d,y)满足市场出清条件 则这个资源配置就是可得的。在市场出清条件中,银行的个体不确定性冲击α也作为预期的对象,这是因为它的横截面分布被假定为与总体不确定性的概率分布相同。不等式(11)是说,在时期1的消费总需求小于或等于短期资产的供给。严格小于的情况是可能的,因为在时期0过度供应的流动性会被重新投资于短期资产而在时期1消费。方程式(12)是说,在时期2的总消费等于银行对于长期资产的投资加上在时期1对于短期资产的投资。一个价格函数如果满足条件,即对于几乎所有的状况δ都有p(δ)≤1并且p(δ)<1意味着(11)式为等式,那么这个价格函数就是可接受的。这样,一个均衡就可以定义为由一个可得的资源配置(m,ρ,d,y)和一个可接受的价格函数p(·)所构成,其中给定价格函数p(·)时,对于每一组消费者i=1,…,m来说,(di,yi)是最优的。 考虑一个没有总体内在不确定性,即ε=0的经济,这个经济只会有外在的总体不确定性,如太阳黑子影响。这样的经济体可以称为极限经济,因为外在不确定性可以视作内在不确定性的极限情况。依照外在不确定性的影响情况,极限经济中的均衡可以划分为三种。一种是基础均衡的情况,这种均衡(m,ρ,d,y)要求消费x(di,yi,α,δ)对于每一个i和α都几乎可以确定为常数,并且p(δ)也几乎可以确定为常数。在这种均衡情况下,太阳黑子变量δ就对均衡价值没有影响。另一种是太阳黑子影响的平凡均衡,这种均衡(m,ρ,d,y)要求消费x(di,yi,α,δ)对于每一个i和α都几乎可以确定为常数但是p(δ)则并不几乎可以确定为常数。在这种均衡情况下,太阳黑子变量δ对消费均衡没有影响,但是对均衡价格p(δ)有影响。最后一种均衡叫做太阳黑子影响的非平凡均衡,也即是太阳黑子变量δ对消费配置产生某些不可忽略影响的均衡。在这种均衡的情况下,金融危机的发生存在着正的概率可能性。这就为金融脆弱性提供了一种论据,即金融体系的危机能够从外在不确定性中产生。 根据阿伦和盖尔的论述,金融危机是一种系统事件。只当违约银行的数量多到足以影响均衡价格的时候,危机才会发生。当一组银行违约并清算其资产时,它会使得资产价格下降从而导致另外一组银行破产。这种性质在模型中起作用,因为这个模型对应的正是不完全市场的情形:太阳黑子是没有契约合同应对的,即存款合同是无法对应太阳黑子变量的。同样的,也不存在着对应太阳黑子变量的阿罗证券(Arrow Securities)市场。所以,金融机构并不能为防范同太阳黑子变量相联系的资产价格波动而进行保险。如果银行能够交易应对太阳黑子变量的阿罗证券,那么它们就能够为应对资产价格变动现象而保险。所以,在均衡中没有阿罗证券的交易是一回事,但是阿罗证券市场的存在则是另一回事,它会产生作用,即均衡配置是激励有效的,太阳黑子不会产生实质的影响,经济中也不存在危机的可能性。 虽然以上模型的设定以金融产业或金融市场为背景,但是多重均衡模型的理论含义并不局限于某一或某些具体的市场体系。它事实上是一个基础理论的问题,涉及市场放任主义的逻辑边界和政府干预市场的逻辑空间。依据阿罗-德布鲁的一般均衡或者理性预期的卢卡斯均衡,市场体系的内在动力是导向惟一均衡点和帕累托最优的。政府因此并无立场来干预经济,因为其任何行为都是对市场内在动力的扭曲。然而,我们以上两个模型却从内因和外因两个层面证明,市场体系的内在动力会将金融产业或金融市场引导至均衡的多重结果。在戴芒德和戴比威格的模型中,金融市场体系或者达成预期的最优福利均衡或者滑入糟糕的“银行挤兑”均衡完全由作为金融系统内因的存款者信心和机构运作机制自发决定,并不需要什么特别的原因。而在阿伦和盖尔的模型,金融系统的内因状况成为市场体系多重均衡的潜在根据,当外因条件随机出现时,系统内相应地出现多重的均衡结果,金融市场体系因此是脆弱的。既然市场体系过程是一个多重的均衡结果的过程,政府的行为如果能够满足某些约束条件,其福利改进的功能就是不言而喻的(对此我们将另外讨论)。接下来简单说明一下在这个方向上的研究进展。 尽管对消费者作了单位分割,阿伦和盖尔的模型在本质上同戴芒德和戴比威格的模型一样,是一个代表性行为主体模型。因此,模型不可避免的模糊了许多经济和行为的关系,例如银行系统中的管制当局。当存在着银行间市场时,除了阿伦和盖尔已经刻画的资产价格下降机制之外,银行失败的传染过程会通过银行间关系更直接地进行。在2003年发表的论文中,拓木克斯(Tsomocos)试图通过拓展德拜和吉诺克普勒斯(Dubey and Geanakoplos)1992年建构的包含货币和违约的标准一般均衡的不完全市场模型而将银行间关系加入。于是一个竞争性的银行部门就被引入了德拜和吉诺克普勒斯的原始模型。商业银行都是异质的,各自通过其个别风险或个别收益的偏好来加以区别。在资本金要求的具体约束下,假定它们最大化各自的预期利润。所有这些都取决于未来状况,也取决于宏观经济变量如总产出或总的违约情况。在另一方面,在流动性约束的情况下,非银行的私人部门最大化他们的消费效用。模型只需两期,资产在第一期交易,在第二期支付,所以不确定性在第二期消除。在股权市场上人们交易商业银行的所有权股份,同样,银行间借贷在第一期也进行着交易。商品市场和非银行私人部门信贷市场在两期都交易。所有市场的交易都必须“现金预付”并且家庭和银行都允许根据其财务状况而违约破产。通过在各自的目标函数上减去一个线性项,这些违约的家庭和银行得到比例对应的惩罚,银行损失利润,消费者损失效用。运用严谨的数理分析,拓木克斯证明存在着含有正的违约水平的货币均衡。银行失败传染和金融脆弱性也都被刻画为一种均衡现象。在拓木克斯看来,戴芒德和戴比威格的结果是他的模型的一个特例,其中银行是同质的并且失败传染是由于违约极大化了。 在2006年的论文中,古德哈特、苏尼兰德和拓木克斯(Goodhart,Sunirand and Tsomocos)从三个方面进一步改进了拓木克斯的模型。首先,他们引入了资本金违规的可能性及其惩罚以及银行股权的一个二级市场。其次,消费者信贷市场的准入是有限的,因此允许在商业银行经营领域存在多种利率。最后,他们通过取消跨期贷款而代之以跨期借贷市场简化了模型。金融脆弱性在他们丰富了的模型中再次表现为一种自然的均衡现象。 当然,还有其他一些的银行经营的理论文献论及金融脆弱性问题。戴芒德和冉杰(Diamond and Rajan)在2001年的论文中证明为了运作其基本功能,银行必须保持某些包含脆弱性的资本结构。同1983年的戴芒德和戴比威格不同,在这里他们假设由于存款人有抽去现金的特殊才能,导致金融资产是非流动性的。卡恩和桑托斯(Kahn and Santos)在他们2006年的论文中假定总体内在不确定性不再为零,从而在阿伦和盖尔的基础上向前又迈出一步。根据他们的观点,金融脆弱性起源于银行为防范流动性冲击而建立起来的银行间交易市场。 以上这些发展的优点是严谨,数理脉络明晰并且也是简单易懂的。但是,由于这些模型主要都是通过银行行为来说明金融脆弱性的,所以金融脆弱性的概念在这些研究中并不完全一致。例如,阿伦和盖尔对金融体系脆弱的界定是一个小的冲击产生大的不成比例的后果,而拓木克斯则以流动性短缺和银行部门特点来刻画金融脆弱性。对拓木克斯来说,当银行和家庭都有大量实质性违约时,无须全都破产,银行部门的利润就会大幅下降,金融脆弱性自然而然地表现出来。金融脆弱性定义的变动性使得人们对其本质的把握出现一定的困难,但是,模型方法所体现的不完全市场和多重均衡之间的关系的确为分析金融内在脆弱性问题指出了一个方向。 Allen,F.and D.Gale,2000.Financial contagion.The Journal of Political Economy,Vol.108,No.1. Diamond,D.and P.Dybvig,1983.Bank runs,deposit insurance,and liquidity.The Journal of Political Economy,Vol.91,No.3. Diamond,D.and R.G.Rajan,2001.Liquidity risk,liquidity creation,and financial fragility:a theoryof banking.The Journal of Political Economy,2001,Vol.109,No.2. Dubey,P.and J.Geanakoplos,1992.The value of money in a finite-horizon economy:a role for banks.In:P.Dasgupta and D.Gale,Editors.Economic Analysis of Market and Games,M.I.T.Press,Cambridge. Goodhart,C.,P.Sunirand,D.P.Tsomocos,2006.A model to analyze financial fragility.Economic Theory,Vol.27,No.1. Kahn,C.M.and J.A.C.Santos,2006.Who should act as lender of last resort?An incomplete contracts model:a comment.Journal of Money Credit and Banking,Vol.38,No.4. Tsomocos,D.P.,2003.Equilibrium analysis,banking and financial instability.Journal of Mathematical Economics,Vol.39. 【责任编辑:许玉兰;责任校对:许玉兰,杨海文】 F830.2 A 1000-9639(2010)01-0203-06 2009-11-09 国家社会科学基金重点项目(编号:07AJL003) 陆家骝(1954-),男,安徽徽州人,经济学博士,中山大学行为金融与金融经济学研究所、管理学院教授、博士生导师(广州510275);陆 婷(1983-),女,江苏南京人,中山大学管理学院博士生(广州510275)。二、不完全市场冲击的多重均衡模型
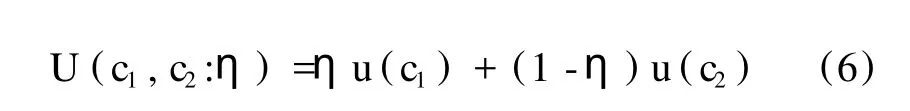



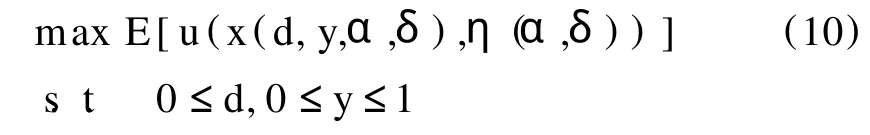
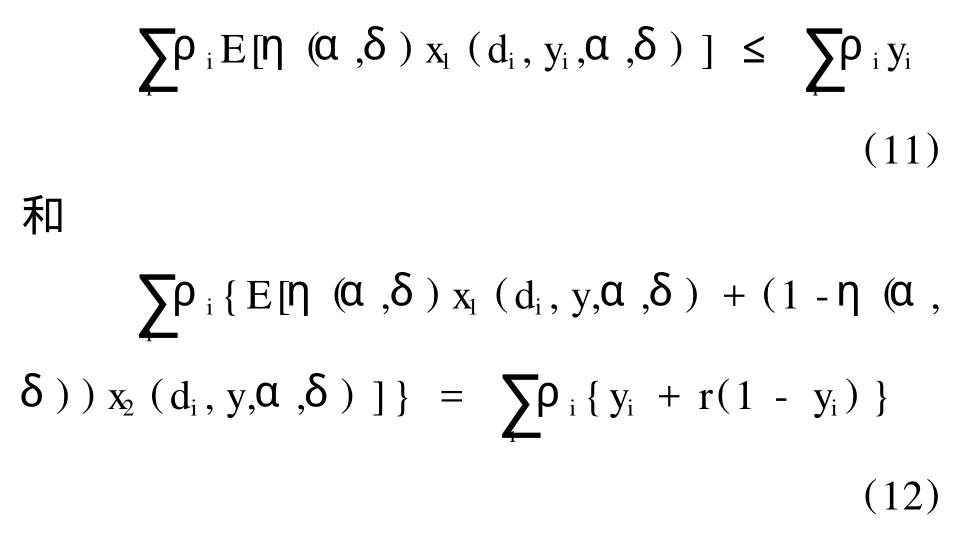
三、多重均衡模型的理论含义与近期发展
- 中山大学学报(社会科学版)的其它文章
- 我国外汇储备若干问题研究*

