变系数模型误差方差的估计
冯井艳,张志强,李华鹏
(山西大同大学数学与计算机科学学院,山西大同 037009)
变系数模型误差方差的估计
冯井艳,张志强,李华鹏
(山西大同大学数学与计算机科学学院,山西大同 037009)
变系数模型是由古典的线性模型发展而来,它们可以很好地检验函数系数随着协变量的变化程度.本文用PLR提出了变系数模型的误差方差的估计,并研究了它的渐近正态性,进一步用一个模拟例子来说明估计的结果是有效的.
变系数模型 误差方差 Profile最小二乘估计 渐近正态性
变系数模型产生于实际需要,它可以很好地探索动态数据特征使得模型更好地拟合数据,因此广泛应用到各科学领域中,比如:经济学,政治学,医药学,生态学等.
Hastie和Tibshirani[1]提出了变系数模型,其定义如下

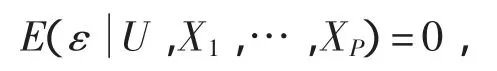
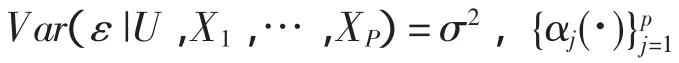
到目前为止,对于具有不同光滑变量的变系数模型的研究还是比较少[4],其定义如下

其中,X=(X1,X2,…,XP)T∈RP,Z=(Z1,Z2,…,ZP)T∈RP为协变量,Y∈R为响应变量,ε为随机误差,且ε与(X,Z)独立,满足E(ε)=0,Va(rε)=σ2.{aα(·)}pα=1是从R到R上的未知可测函数.文献[4]已经估计了函数系数{aα(·)}pα=1,类似的讨论还有文献[5].但是,有时候,对误差方差σ2=E(ε2)的估计的研究也是很有必要的,它可以有利于置信区间的建立,模型检验及选择等.在本文中,由最小二乘法得到了误差方差σ2的估计,并得到了它的渐近性质.
1 估计
假定{Yi,Xi,Zi,i=1,…,n}是模型(2)的一个简单随机样本,{aα(·)}pα=1是Lipschitz连续的,那么a(αXα)在Xα的支撑内的一点xα附近能够用一个线性函数表示,即

关于{aα}pα=1和{bα}pα=1极小化,其中,Xiα,Ziα分别是X,Z的第i个观测值的第α个分量;Kα,hα(·)=h-1αKα(·/ hα),Kα(·)是一个有紧支撑的关于0对称的有界非负的Lipschitz连续的概率密度函数;hα=hnα是一个正数数列,称作窗宽.设(αx),α=1,…,p,是使(3)式达到极小化的前p个值.由最小二乘理论,可得
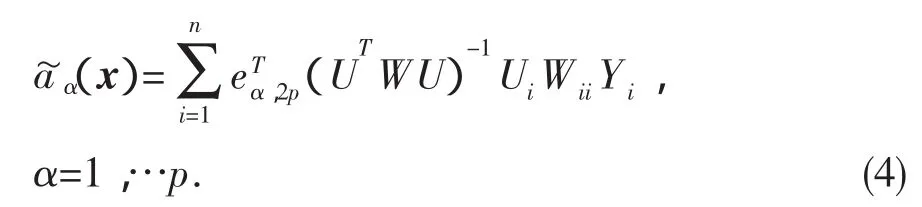
其中x=(x1,…,xp)T,eα,2p是第α个分量为1的单位向量,U是一个n×2p矩阵,它的i行是
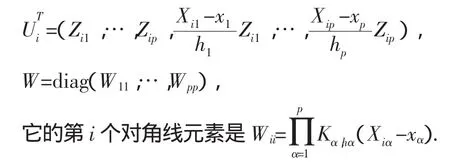
在(4)式的基础上,使用平均方法定义函数系数aα(Xα)的平均估计为

其中,a=(a1(X1),…,ap(Xp))T.我们可以定义误差方差σ2的估计为

2 误差方差的渐近性质
假设:A1随机变量X是有紧支撑的,它的密度函数f(·)是Lipschitz连续有界的,且大于某一正数.
A3存在s,k分别有s>2满足E‖z‖2s<∞,k<2-s-1满足n2k-1h→∞.
A4{aα(·),α=1,…,p}有二阶导数.
A5核函数K(·)是有紧支撑的,关于0对称的,有界非负的Lipschitz连续的概率密度函数;窗宽h满足nh8→0,nh2(/log n)2→0.
定理1若假设 A1~A5成立,如果Eε41<∞,E‖X1‖4<∞,当n→∞时,则有

定理2若假设 A1~A5成立,如果Eε41<∞,当n→∞时,则
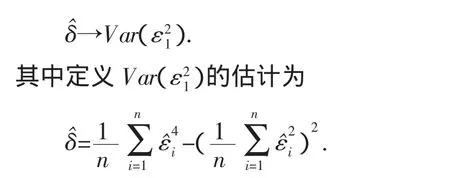
推论1在定理1和定理2的条件下有
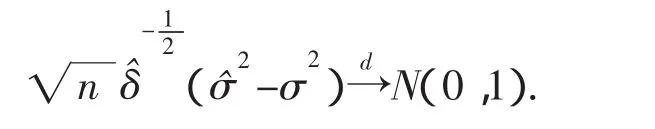
3 模拟
这一节我们应用Monte Carlo模拟方法来说明如上提出的估计方法的有效性.假定模拟例子为:

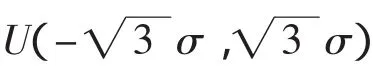
4 证明过程

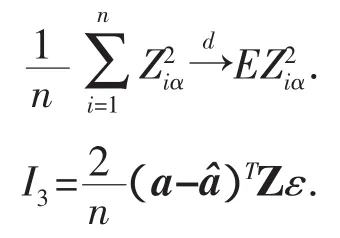
它的证明类似于Zhou和You[6]的定理3.2的证明.则有I3=οp(1).定理1证毕.
表1 2的均值和标准误差

表1 2的均值和标准误差
■ σ)σ2 0.04 0.25 0.64 0.04 0.25 0.64 Mean 0.057 0.072 0.533 0.073 0.836 0.065 SD 0.009 0.038 0.085 0.006 0.029 0.075 ε~N(0,σ2) ε~U(- 3■ σ, 3
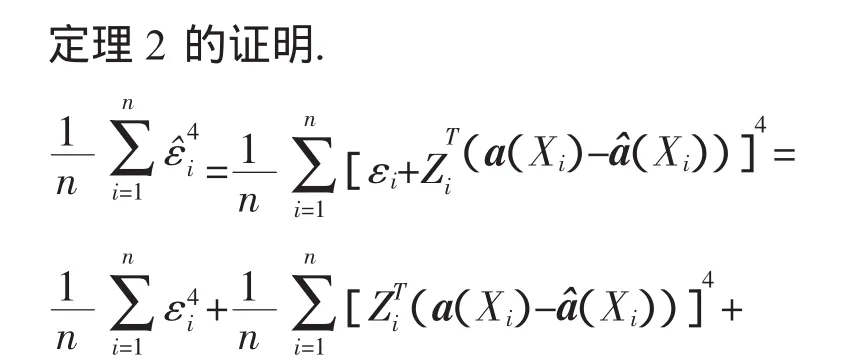

则,J3=οp(1),J4=οp(1),J5=οp(1).则只需证明 J2=οp(1),它的证明类似于I2=οp(1)的证明,则定理2证毕.
[1]Hastie T,TibshiraniR.Varying-coefficientmodels[J].Royal Statistical Society,2003,55(4):757-796.
[2]Hoover D R,Rice JA,Wu C O,et al.Nonparametric smoothing estimates of time-varying coefficientmodels with longitudinal data[J].Biometrika,1997,85:809-822.
[3]Fan J,Zhang J.Functional linearmodels for longitudinal data[J].JRoy Statist Soc B,2000,62:303-322.
[4]Zhang Riquan,Li Guoying.Efficient estimation of functional-coefficient regression models with different smoothing variables[J].Acta Mathematica Scientia,2008,28B(1):989-997.
[5]张日权,张志强,冯井艳.一类新的变系数模型的积分估计[J].山西大同大学学报:自然科学版,2007,23(5):1-5.
[6]Zhou X,You J.Waveletestimation in varying coefficientpartially linear regressionmodels[J].Statist probab Lett,2004,68:91-104.
Error V ariance E stimation of V arying C oefficient M odels
FENG Jing-yan,ZHANG Zhi-qiang,LIHua-peng
(School ofMathematics and Computer Science,ShanxiDatong University,Datong Shanxi,037009)
Varying coefficientmodels are a useful extension of classical linear models.These models can easily examine how regression coefficient change over different groups characterized by certain covariates.In this article,the estimator of error variance by profile least-squares procedure is proposed and its asymptotic normality is studied.Furthermore,some simulations are conducted to examine the performance of our estimating approach and the results are substantial.
varying coefficientmodels;error variance;profile least-squares estimation;asymptotic normality
O212.7
A
〔编辑 高海〕
1674-0874(2010)01-0005-03
2009-11-30
国家自然科学基金项目[10871072];山西省自然科学基金项目[2007011014]
冯井艳(1982-),女,山西太原人,硕士,助教,研究方向:数理统计.

