用弧微分向量证明重积分换元定理
施泱
(山西大学工程学院,山西太原 030013)
用弧微分向量证明重积分换元定理
施泱
(山西大学工程学院,山西太原 030013)
利用曲线坐标系中的弧微分向量,建立了坐标系变换中面积元素与体积元素之间的关系,从而给出了重积分换元定理的简洁证明方法.
弧微分 面积元素 体积元素 换元法
传统的重积分换元定理的证明方法是从几何的角度建立不同坐标系下面积微元、体积微元的联系,证明过程非常繁琐.本文利用微分及弧微分的概念,引入一种无穷小向量,弧微分向量,并利用向量的向量积及混合积为工具,直接建立了坐标系变换中,面积元素、体积元素之间的关系
1 二重积分换元定理的证明
定理1 设f(x,y)在xoy平面上的闭区域D上连续,变换T∶x=x(u,v),y=y(u,v),将uov平面上的闭区域D′变为xoy平面上的闭区域D,且满足
(1)x=x(u,v),y=y(u,v)在D′上具有一阶连续偏导数;
(2)在D′上雅可比式

(3)变换D′→D是一对一的则有
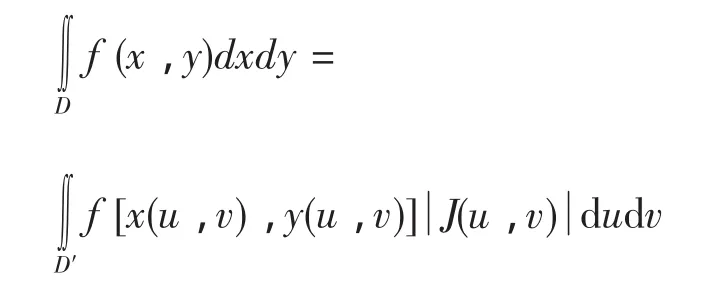


图1 直角坐标变换图
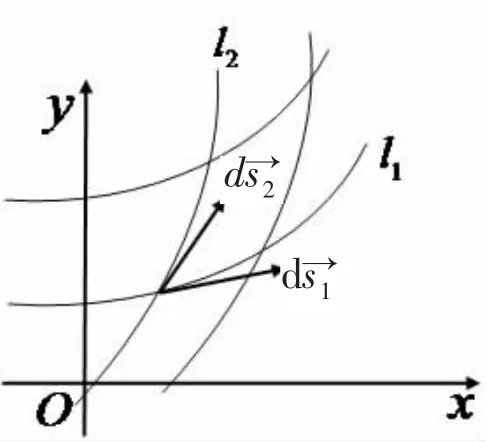
图2 弧微分向量变换图


2 三重积分换元定理的证明
定理2 设f(x,y,z)在空间oxyz上的闭区域Ω上连续,变换T∶x=x(u,v,w),y=y(u,v,w),z=z(u,v,w)将空间ouvw上的闭区域Ω′变为oxyz上的闭区域Ω,且满足
(1)x=x(u,v,w),y=y(u,v,w),z=z(u,v,w)在Ω′上具有一阶连续偏导数;
(2)在Ω′上雅可比式
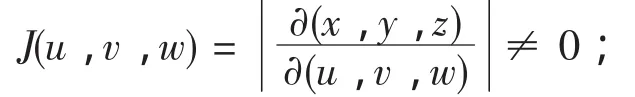
(3)变换Ω′→Ω是一对一的
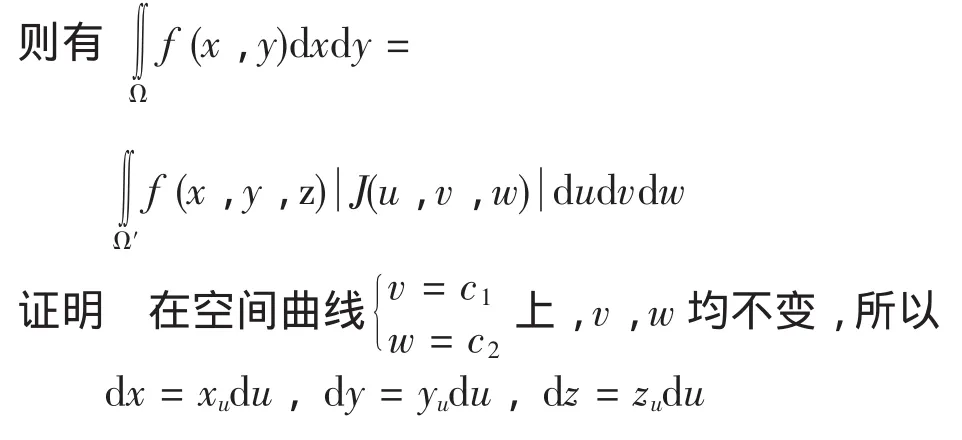

[1]谢树艺.矢量分析与场论[M].北京:高等教育出版社,2007.
[2]陈纪修,於崇华,金路.数学分析[M].北京:高等教育出版社,2000.
[3]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.
[4]冯文强,杨汉生.二重积分换元法的另一种证法及推广[J].西南科技大学高教研究,2006(4):69-74.
[5]李开丁,李莉.定积分的二种换元法及其应用[J].高等数学研究,1999(4):15-18.
[6]梅银珍,王鹏,李有文.二重积分换元公式的一种简便推导方法[J].华北工学院学报,2004(3):166-168.
A Proof of M ultip le Integral Substitution Theorem by Arc Differential Vector
SHIYang
(Engineering College,ShanxiUniversity,Taiyuan Shanxi,030013)
By using the arc differential vector of curvilinear coordinate system,this paper establishes the relationship between area elementand volume element,and thus presents a simplermethod of provingmultiple integral substitution theorem.
arc differential;area element;volume element;substitution
O177.6
A
〔编辑 高海〕
1674-0874(2010)04-0018-02
2010-04-23
施泱(1968-),男,山西太原人,讲师,研究方向:基础数学.

