一种基于逆序编码的关联规则挖掘研究

王 盛,董黎刚,李 群

(浙江工商大学信息与电子工程学院,浙江杭州310018)

0 引 言

关联规则是数据挖掘一个重要课题。数据预处理是数据挖掘中的一个重要阶段。数据预处理的目的就是找到一种高效的方法来存储数据,以使对数据子群的访问尽可能快。但人们往往忽略它对数据挖掘的重要性,使它经常成为整个数据挖掘算法的瓶颈[1]。当前的规则挖掘算法[1-6]主要从3个方面着手：(1)如何降低规则挖掘的扫描开销;(2)如何减少扫描事务数据库的次数;(3)如何确定频繁项目集并减少候选项目个数和计算频繁项目集的支持数。如基于二进制序列集挖掘算法[2],B-Apriori算法[1],采用PLT结构的算法[4],采用剪枝技术的Apriori改进算法[5]等,这些算法中有些改进了数据预处理技术,而确定繁项目集仍沿用运算量大的Apriori算法中的方法。对于新增加的项目,新老数据无法相互兼容,必须整体重新扫描生成数据,这种特性降低了效率,同时增加了系统的开销。因此,针对以上3个方面及算法存在的不足,必须寻找一种安全、高效的实现方式对数据进行分析,目前国内外并没有较好的研究报道。为此,本文提出一种基于二进制数以及项目的支持度分布(概率分布)的Apriori改进算法BF-Apriori。

1 主要定义和性质

为了实现BF-Apriori算法,定义1规定了对数据库中的数据进行二进制数转换的转换协议。相关的性质为规则挖掘算法的相关运算保证了理论依据和运算结果的可靠性。

定义1 事务-二进制数逆序转换关系RTR,给定项目集I={I1,I2,…,Im},其中项目是按照项目支持度从大到小排列。事务数据库D,其中T∈D,并且T⊆I,规定f1：T×I→bk…b3b2b1(k≤m,且为事务t中包含的项目编号的最大值),并称b=bk…b3b2b1事务T所对应的二进制数,记为Bt,其中bj∈{0,1},若事务中包含Ij则bj=1,否则为0。

性质1 行向量逆序转换性质,给定项目集I={I1,I2,…,Im},若二进制Bt的第j1,j2,…,jk(ji＞ji-1,且0＜j≤m,1≤i≤k,其中 jk为b的最高位的序号)位的值为1,则Xb={Ij1,Ij2,…,Ijk},其中jk小于等于Bt的最高位。

证明 根据RTR转换规则,性质1显然成立。

性质2 给定项目集 I={I1,I2,…,Im},假设事务二进制数Bt1、Bt2,如果Bt1and Bt2=Bt1,那么事务T1⊆T2。

证明 根据逻辑与的定义和定义1,性质2显然成立。

性质3 若某一元素在产生的所有频繁项集Xk-1中出现的次数小于k-1次,那么它就不可能是频繁项集Xk的元素。

证明 由频繁项集的定义可知,频繁项集的任一子集都是大的,根据排列组合的性质可知,频繁项集Xk的k-1维子集也就是意味着在k个元素中去掉一个,那么每一个元素在Xk的k-1维子集中出现的次数等于k-1次,所以若某一元素在产生的所有频繁项集Xk-1中出现的次数小于k-1次,那么它就不可能是频繁项集Xk的元素。性质3得证。

2 数据处理和规则挖掘

假设I={I1,I2,…,Im}是m个不同项目的一个集合,T={t1,t2,t3,…,tn}是事务数据库D中n条记录的集合,minsup表示最小支持度,X.sup表示项目集X在事务数据库D中所对应的支持数,Li表示频繁i项目集,Fre表示上一级挖掘中每一个项目成功组合的次数,Cas表示事务总数,R表示满足minsup的组合,NFre表示当前挖掘中每一个项目成功组合的次数。

2.1 以二进制数转换事务数据库的算法

算法1 基于二进制数的行向量转换事务的算法(RTR算法)。

对于海量的数据,采用内存管理当中的地址映射中的组相联策略,可对所得到的数据进行切片运算,即事务经过行向量转换得到二进制数过长,则对其进行定长截取并进行标记,分别进行支持度或支持数的统计,得到的结果再进行组合从而得到总的支持度和支持数。

由于项目在事务当中的发生的不确定性,因而本文对于事务-二进制数逆序转换算法在空间上的性能做了如下的理论估计。

假设项目集I={I1,I2,…,Im},事务数据库D,其中T⊆I且T⊆D,对应的支持度(也就是概率)分别为P={P1,P2,…,Pm},且项目集中的各项目支持度之间的关系是P1＞P2＞…＞Pm,则事务的平均长度的：

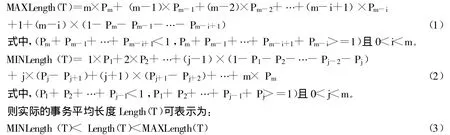
根据定义1,本文给如图1所示的RTR转换算法流程图。

2.2 规则生成频繁i-项目集算法

算法2 行向量逆序转换后规则挖掘算法BF-Apriori(RTR)(BF-Apriori based on RTR)如图2所示：

3 算法实现和性能比较

为了验证算法的性能,本文用JavaSE-1.6在内存2G、CPU为 Intel酷睿 2双核T7500 2.2GHz、操作系统为Windows7 Ultimate的电脑上实现算法,本文使用了与文献6同样的测试数据库对算法进行实现和性能分析,该数据库有8124条记录,记录了Mushroom的23种属性119个属性分量。

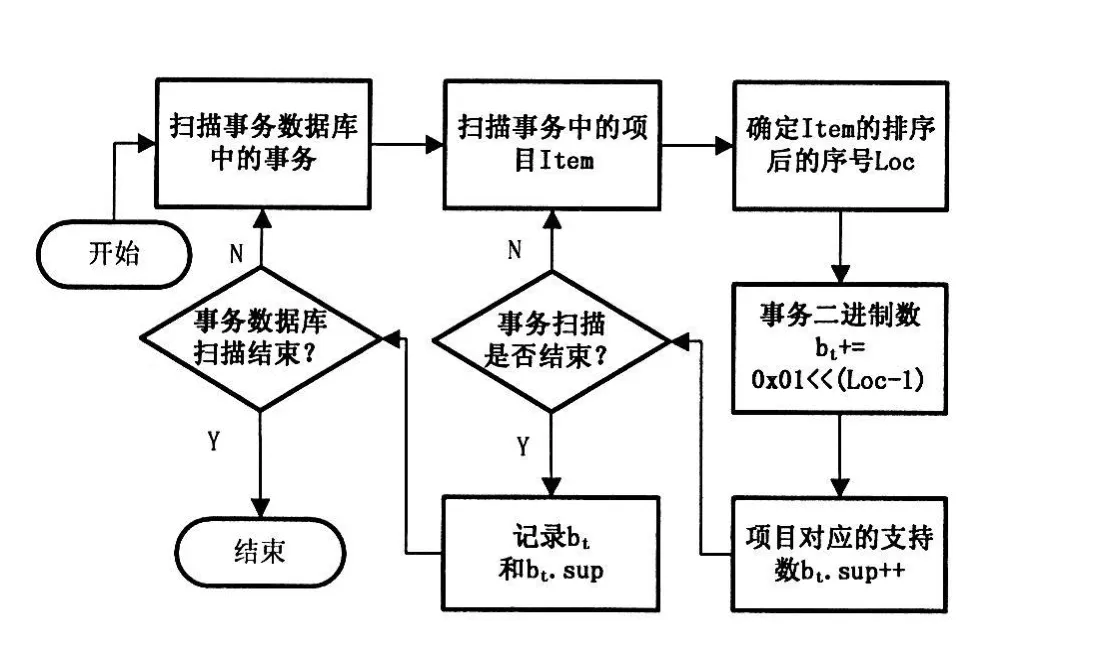
图1 RTR转换算法流程图

图2 BF-Apriori(RTR)算法

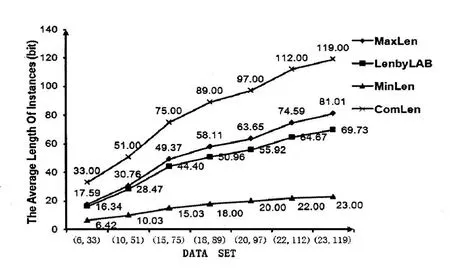
图3 逆序转换长度比较

3.1 算法预处理的验证实验

为了验证RTR算法事务平均长度估计公式的准确性、RTR算法的高效性,在实验的过程中,本文取了7组数据集(6,33)、(10,51)、(15,75)、(18,89)、(20,97)、(22,112)、(23,119)。其中(属性数,分量数),MaxLen由公式1计算得到RTR转换的估计的事务平均长度的最大值,MinLen为由公式2计算得到RTR转换的估计的事务平均长度的最小值,LenbyLAB为实验测得事务的平均长度,ComLen为一般基于二进制序列的算法[2]事务的平均长度,实验的结果如图3所示。

通过图3可以看到,经过RTR转换后事务的平均长度明显优于其他基于二进制序列的数据预处理方法,基于Mushroom数据库的RTR转换节约了50%左右的存储空间,可见,RTR算法比一般的基于二进制数据预处理方案在存储开销上优越。此外,从实验可以得出事务经RTR转换的事务平均长度LenbyLAB落在了MaxLen,MinLen之间,从而证明在实践中式1、2可以用来估计经RTR转换的事务的平均长度区间并定性分析RTR算法的性能。

3.2 规则挖掘算法验证实验

为了验证算法规则挖掘的性能,本文在电脑上实现了BF-Apriori(RTR)算法和B-Apriori算法(该算法与本算法属于同一类型)[1]生成频繁项目集并计算项目集的支持数。分别取了 0.05、0.08、0.11、0.14、0.17、0.20、0.25、0.30、0.35、0.45、0.50、0.60这12组支持度进行频繁2-项目集挖掘(2层关联挖掘),联规则挖掘的算法实际执行时间如图4所示。

图4可以看出,BF-Apriori(RTR)的挖掘效率比一般的B-Apriori算法提高了一个数量级。随着最小支持度的增大,BF-Apriori(RTR)算法的执行效率明显提高,B-Apriori算法也有提高,但提升幅度没有BF-Apriori(RTR)算法突出,从而验证了BF-Apriori算法的有效性和高效性。

4 结束语

本文提出一种基于二进制数以及项目的支持度分布的Apriori改进算法BF-Apriori。该算法能够将事务信息进行大幅度压缩后存入内存,提高规则挖掘的效率,同时能够很好的将二进制数回溯到事务记录。在分布式数据分析时,只要双方同步数据字典(项目的排序定义),就能够实现基于网络的加密的分布式数据分析,同时,BF-Apriori(RTR)算法具有数据高可压缩性和可分割性,能大幅降低分布式系统间的通信量,对于新增加的事件类型,能够兼容已转换的数据而无需重新生成。实验结果表明,BF-Apriori算法提高数据挖掘算法中项目集的存储效率,比基于二进制序列的处理方法效率提高了将近一倍。而在进行2层关联挖掘方面,挖掘效率提升了一个数量级。BF-Apriori算法为海量数据库的知识发现提供了一种高效而快速的算法。

图4 二层关联规则挖掘的算法执行时间

[1]陈耿,朱玉全,杨鹤标,等.关联规则挖掘中若干关键技术的研究[J].计算机研究与发展,2005,42(10)：1 785-1 789.

[2]孔令富,王晗,练秋生.一种基于关联规则挖掘的组织数据方法[J].计算机工程,2006,32(21)：12-14.

[3]颜跃进,李舟军,陈火旺.一种挖掘最大频繁项集的深度优先算法[J].计算机研究与发展,2005,42(3)：462-467.

[4]Azzedine Boukerche,Samer Samarah.A Novel Algorithm for Mining Association Rules in WirelessAd Hoc Sensor Networks[J].IEEE Transactions On Parallel And Distributed Systems,2008,19(7)：865-877.

[5]何海涛,吕士勇,田海燕.基于改进 Apriori算法的数据库入侵检测[J].计算机工程,2009,35(16)：154-158.

[6]宋余庆,朱玉全,孙志挥,等.基于FP-tree的最大频繁项目集挖掘及更新算法[J].软件学报,2003,14(9)：1 586-1 592.