双孔盾构隧道地表位移离心机模型试验研究

孙 兵,仇文革

(1.中铁第一勘察设计院集团有限公司桥隧处,西安 710043;2.西南交通大学土木工程学院,成都 610031)

双孔盾构隧道地表位移离心机模型试验研究

孙 兵1,仇文革2

(1.中铁第一勘察设计院集团有限公司桥隧处,西安 710043;2.西南交通大学土木工程学院,成都 610031)

采用室内离心模型试验模拟双孔盾构隧道近接施工,通过定量控制隧道外套的水囊注放水的方式模拟盾构隧道的地层损失。研究了横断面地表沉降的量值、分布规律以及随盾构推进距离的变化规律,并提出相应防护措施。结果表明：水囊注放水方法可以有效模拟盾构隧道地层损失;盾构推进距离和隧道相对位置关系对地表沉降的量值和分布规律有显著影响。

双孔盾构隧道 近接施工 离心模型试验 地表位移

0 前言

随着城市的快速发展,大量地下工程及隧道的近接施工问题是不可避免的。目前,对于近接施工问题的设计和施工还无规范和标准可循,结构加固和防护措施要求往往过于严格,会造成施工困难和经济损失。再加上盾构技术的广泛应用,因此,研究盾构隧道近接施工问题已成为当务之急。目前,在盾构施工引起的地表沉降的预测中,常规的方法有经验公式、数值模拟和模型试验。周小文等利用橡皮囊充气再放气的办法进行了多组南水北调引黄盾构隧道的离心模型试验,研究了隧洞内支护压力与地层位移的关系,施工间隙的影响,以及砂层稳定与破坏的机理[1-2]。马亮、刘庆舒等用融化石蜡的方法在离心机上模拟了矿山法隧道的开挖[3-4],对应力场和渗流场耦合下的地表沉降进行了研究。大量的研究和工程实践表明,在盾构施工中的地表沉降与地层损失直接相关。很多预测地表沉降的经验公式均与地层损失建立了联系,如 1969年Peck提出的高斯分布曲线[5],国内同济大学提出的考虑施工间隙和固结因素的横向沉降量 Peck修正公式[6],以及刘建航院士提出的预测纵向沉降的修正Peck公式等[7]。作者前期曾采用三维数值模拟方法,对三管盾构隧道下穿铁路引起的地表位移及其控制技术进行了研究[8]。本文采用室内离心模型试验方法,通过水囊注放水方法模拟盾构隧道掘进中的地层损失,对双孔盾构隧道在不同相对位置情况下所引起的地表沉降进行了研究。分析了横断面地表沉降的量值、分布规律以及随盾构推进距离的变化规律,并提出相应的防护措施,保证工程的安全,为类似工程提供服务,具有很强的学术和工程意义。

1 试验方案和试验模型

1.1 试验设备

试验设备为西南交通大学土工离心试验机。该设备主要参数如下：①100g◦t;②有效半径 2.7m;③模型箱有效尺寸 0.8 m×0.6 m×0.6 m,0.6 m×0.4 m×0.4m;④离心机的工作范围 10～200g;⑤允许连续工作 12 h;⑥测量模式：传感器 +放大器 +智能测量仪 +数据数字化并行传输 +集流环 +数据接受和处理终端(计算机);⑦通过摄像系统可以监视和记录试验全过程。

1.2 模型试验域及相似比的确定

选择 0.6m×0.4m×0.4m的模型箱。考虑到二个隧道的尺寸和空间位置,以及边界效应的影响,根据模型箱的尺寸,选定本次试验的几何相似比为 1∶100,试验域的几何尺寸如表 1所示。根据离心机模型试验的基本原理和 Buckingham的 π定理,各物理量相似比如表 2所示。

表1 试验域取值 m

表2 参数的相似比(原型/模型)

1.3 试验材料选取

地层填料选用原状土。地层多为黏土,材料力学参数见表 3。根据地勘报告中的相应含水量进行重塑,并在离心机上固结来完成,通过剪切试验控制其c、φ指标。对于盾构隧道衬砌结构,若采用原型混凝土材料导致结构过薄(3.5 mm),难以满足要求。因此,按照等效刚度相似原则选用与钢筋混凝土密度、泊松比相近,且物性稳定的 LYZ型铝材作为相似材料,经计算所需铝材模型衬砌的厚度为 2.5 mm,铝材弹性模量E=70GPa,泊松比 μ=0.3,相似准则推导参见文献[2]。

表3 各土层的物理力学参数

1.4 位移测试原件和测试点的布置

试验采用由北京鸿基点科技发展有限公司生产的MDA-5系列直线位移传感器。测杆形式为弹簧复位,量程 10 mm,精度 0.1%F◦S,电源 ±12 VDC,输出 0～5 VDC,共 5支。测试点布置在纵向中心断面处,具体位置如图 1所示。

1.5 地层损失及模拟方法

试验采用水囊注放水的方式模拟盾构掘进的地层损失。水囊用高强度橡胶制作,单层厚 1 mm,外径 64 mm,内径 62mm,每段长 60mm,每段设 1000 mm长导管,出口处设阀门。根据文献[9],地铁盾构施工的地层损失率一般可取为 0.3%～0.6%,结合本工程实际情况,可取为 0.5%。由盾构机的直径 6.34 m,可算得每延米的地层损失量为 0.158 m3,由几何相似比得到60mm长水囊的释放水量为 0.95 ml,取为 1ml。根据理想气体的状态方程—克拉伯龙方程,当压力增大到100倍,空气将压缩为原来的 1%,因此,注入水量以注满为准,此时由空气压缩产生的影响将可以忽略。将注水后的水囊逐个套在隧道衬砌模型的外侧。

图1 工况一地层及传感器布置示意(单位：mm)

1.6 试验工况及过程

如图 2所示,根据两隧道相对位置共有 4种工况。对于工况一、二,先施工左线隧道(1号隧道),再施工右线隧道(2号隧道),3号位移传感器位于两隧道中心正上方;对于工况三、四,先施工下线隧道(1号隧道),再施工上线隧道(2号隧道),3号传感器位于 1号隧道中心正上方。

图2 模型试验工况示意(单位：mm)

试验步骤如下：

1)关闭离心机室装甲门,启动离心机,逐渐增大其转速使加速度至 100g,持续一小时(相当于原型 417 d),以模拟土层固结。观察各位移传感器读数,如果读数未进入量程,记录差值,待停机后调整位移传感器位置,使读数进入量程。

2)减速至停止,打开装甲门,用导管和注射器抽出1号隧道的 1、2号水囊中的 1 ml水,在 100g下持续运转 10 s(相当于原型 27.8 h),动态采集的采样频率设为0.03 k,静态采集存储时间间隔为 1 s,记录读数。

3)减速至停止,打开装甲门,用导管和注射器抽出 1号隧道的 3号水囊中 1 ml水,其余与(2)相同。

4)减速至停止,打开装甲门,用导管和注射器抽出 1号隧道的 4号水囊中 1 ml水,其余与(2)相同。

5)减速至停止,打开装甲门,用导管和注射器抽出 1号隧道的 5、6号水囊中各 1 ml水,其余与(2)相同。此时,1号隧道施工模拟结束。

6)～9)步为施工 2号隧道步骤,与 2)～5)步相同。

2 试验结果分析

根据试验数据,绘出各测点地表沉降随水囊释放位置(盾构推进距离)的变化曲线,以及不同试验步骤下的地表横断面沉降曲线。如图 3、图 4所示,图中水囊释放位置 0～40(模型：cm,原型：m)为 1号隧道盾构推进距离,40～80(模型：cm,原型：m)为 2号隧道盾构推进距离。从图中可以看出：

图3 各工况测点地表沉降随释放水囊位置变化

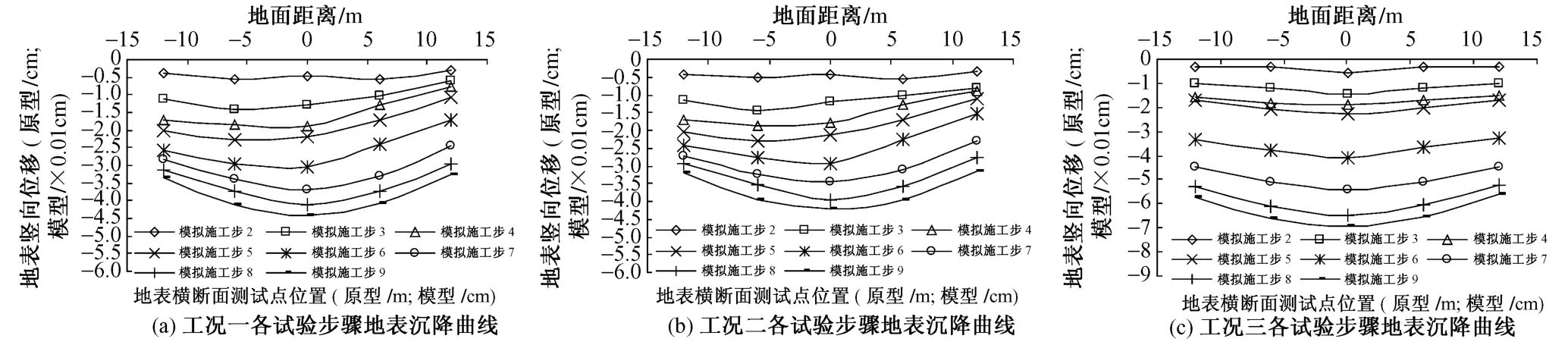
图4 各工况试验步骤地表沉降曲线

利用水囊注放水方法可有效模拟盾构掘进的地层损失,从而研究盾构施工所引起的地表沉降。

各测试点地表沉降随盾构推进距离的增大而增大。

对于水平近接隧道,1号隧道施工时,测点 1、2、3地表沉降增大较快,其中测点 2地表沉降最大。2号隧道施工时,测点 3、4、5地表位移增大较快,且测点 3地表沉降超过测试点 2成为最大沉降。可知,最大地表沉降发生在两隧道中心所对应的地表处,且地表最大沉降随两隧道净距的减小而增大。

对于上下重叠隧道,1号隧道施工时,测点 3(隧道正上方)的地表沉降最大。2号隧道施工时,测点 3附近地表沉降增大较快,且 2号隧道开挖所引起的地表沉降大于 1号隧道。工况四的地表最大沉降发生在2号隧道上方,其量值随两隧道相对位置的变化而变化,水平间距越大,地表最大沉降越小。

上下重叠盾构隧道施工对地表沉降造成的影响大于水平盾构近接隧道。

3 对策措施

铁路部门提出的允许沉降是 10～30mm。因此,上述四种近接隧道施工造成的地表沉降均超限,特别是考虑到在粘土中的地层需要经历一个长期的固结和次固结过程。因此,为控制地表沉降,需进行地层加固,提高地层的强度和防渗性能,进而抑制盾构机通过时的松动范围,从而防止地层变位超限。施工过程中加强盾构机壁后同步注浆,可以有效的填充盾构机推进时所造成的地层损失,确保隧道管片衬砌的早期稳定,外力作用均匀,提高隧道的抗渗性。同时,施工过程中应加强对地表、建筑物和邻近已建隧道的监控量测,合理调整施工方法,从而达到在满足工程进度的同时确保地面和邻近地下建筑物的结构安全。还要与铁路部门紧密配合,必要时结合铁路的养护工作,通过起道调整线路平纵参数。

4 结论

通过对上述双孔盾构隧道地表位移离心机模型试验研究,得到以下结论：

1)利用水囊注放水方法可以有效模拟盾构掘进的地层损失,从而研究盾构施工所引起的地表沉降。

2)各测点地表沉降随盾构推进距离的增大而增大。

3)对于水平近接隧道,最大地表沉降发生在两隧道中心所对应的地表处,且地表最大沉降随两隧道净距的减小而增大。

4)对于上下重叠隧道,地表最大沉降发生在 2号隧道上方,其量值随两隧道相对位置的变化而变化,两隧道水平间距越大,地表最大沉降越小。

5)上下重叠盾构隧道施工对地表沉降造成的影响大于水平盾构近接隧道。

6)为控制地表位移,要严格控制施工措施,同时,施工过程中应加强对地表、建筑物和邻近既有隧道的监控量测。

[1]周小文,濮家骝,包承钢.隧洞拱冠砂土位移与破坏的离心模型试验研究[J].岩土力学,1999,20(2)：32-36.

[2]周小文,濮家骝.隧洞结构受力及变形特征的离心模型试验研究[J].清华大学学报,2001,41(8)：110-113.

[3]马亮,高波.隧道施工地表沉降控制的离心模型试验[J].施工技术,2005,34(6)：6-8.

[4]刘庆舒.用离心模型试验研究地铁施工引起的固结沉降[J].四川建筑,2003,23(5)：32-33.

[5]Peck RB.Deep excavations and tunneling in softground[A].Proceedings Of the 7th International Con ference on soil Mechanics and Foundation Engineering[C].Mexico City：State of the Art Volume,1969：225-290.

[6]侯学渊,廖少明.盾构隧道沉降预估[J].地下工程与隧道,1993(4)：24-32.

[7]刘建航,候学渊.盾构法隧道[M].北京：中国铁道出版社,1991.

[8]郑余朝,仇文革,张俊儒.三管盾构隧道下穿铁路引起的地表位移及其控制技术[J].中国铁道科学,2007,28(5)：65-70.

[9]沈培良,张海波,殷宗泽.上海地区地铁隧道盾构施工地面沉降分析[J].河海大学学报,2003,31(5)：556-559.

TU455;TU317+.1

A

1003-1995(2010)02-0038-04

2009-09-09;

2009-09-30

国家自然科学基金资助(项目批准号：50578135)。

孙兵(1981— ),男,沈阳市人,博士研究生。

(责任审编 赵其文)