盾构在道路和铁路下推进引起的沉降对比研究

王国栋，肖 立，张庆贺

(1.天津滨海快速交通发展有限公司，天津 300457;2.同济大学 岩土及地下工程教育部重点实验室，上海 200092;3.同济大学 地下建筑与工程系，上海 200092)

随着盾构施工技术的不断完善，盾构法施工已经成为城市地铁建设中的一种重要方法。但是，由于地质条件和施工工艺的限制，盾构掘进不可避免的会对周围土体产生扰动，产生地面沉降［1］。目前对地表沉降的研究大致分为经验公式法、模型试验法和数值模拟法等［2-4］。经验公式法主要是 Peck 公式［2］，该法假定地面沉降的横向分布类似正态分布曲线，且沉降槽的体积等于地层损失的体积。许多工程实例也证明了它的实际使用效果。但该公式中参数的选取带有经验性，未考虑土层条件和施工过程。模型试验法是研究盾构隧道施工问题的有效手段，但因造价较高、难度较大而很少采用。数值模拟法可以模拟施工的主要步骤，并且可以对盾构掘进各阶段对周围环境的影响作出定量的分析，应用越来越广泛。但是数值模拟法存在较多的假设，这就可能造成结果的失真，另外，参数的选取也存在较大的主观性，故数值模拟法多用于校核监测得到的规律。地铁建设的不断发展使得盾构穿铁路的情况时有发生，但是以上方法中对盾构下穿铁路时造成的地基沉降规律研究不是很多［5］，尤其是对盾构长距离穿越多条铁路股道的情况更是鲜有涉及。因此有必要对此领域开展研究，以探求地表变形规律。

1 工程概况

津滨轻轨西段地下线工程，西起市区天津站，东接已建成并投入运营的河东区中山门站。天津站—七经路站为盾构施工区间段，该区间段沿线两侧建筑物较多，地下管线复杂，地面交通比较繁忙，盾构掘进施工中须穿越天津站全部铁路股道(23条)，是西段工程五个区间段中最困难的施工段之一。工程采用土压平衡式盾构机掘进，盾构施工时左右线均以七经路站为始发井，天津站为接收井。第一台盾构右线掘进一个月即试验段掘进完后，第二台盾构开始左线掘进。管片外径6 200 mm，内径5 500 mm，厚 350 mm，长1 200 mm，每环由6块组成，错缝拼装。主要土层自上而下依次为①填土、③3黄色粉质黏土、④4灰褐色粉质黏土、④5黄灰色粉土、⑤1灰色粉质黏土、⑥2灰黄及灰绿色粉质黏土、⑦1黄褐色粉质黏土、⑦5黄色粉砂、⑧2灰褐色粉质黏土、⑨7灰黄色粉砂、⑩黏土。浅层地下水属孔隙潜水，埋深为0.5～3.8 m。

2 监测方案

为确保津滨轻轨西段地下工程天津站～七经路站盾构区间隧道施工任务的顺利完成，对整个区间段实施了地表沉降全程监测。具体监测方案如下。

1)盾构沿道路推进

盾构穿越城市道路段地表沉降监测点沿盾构左右两线轴线布置，每4环(4.8 m)设置一个纵向测点，每24环(28.8 m)设置一组横向测点，采用精密水准仪测量。地表监测点的布设如图1，图2所示。

2)盾构在铁路下方推进

盾构穿越铁路股道段地表沉降监测点沿盾构左右两线轴线布置，设置14组横向测点。由于站场内铁路运输比较繁忙，无法做到长时间进入站场，地表沉降监测采用精密静力水准系统，进行数据的数字化采集。如图3所示。

地表沉降监测点布设如图4，图5所示。

图1 盾构穿越道路段地表监测点布设平面

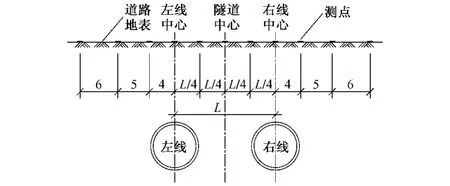
图2 盾构穿越道路段地表横向监测点布设剖面

图3 静力水准仪及布设

图4 盾构穿越铁路股道段地表监测点布设平面

3 监测结果

3.1 纵向沉降

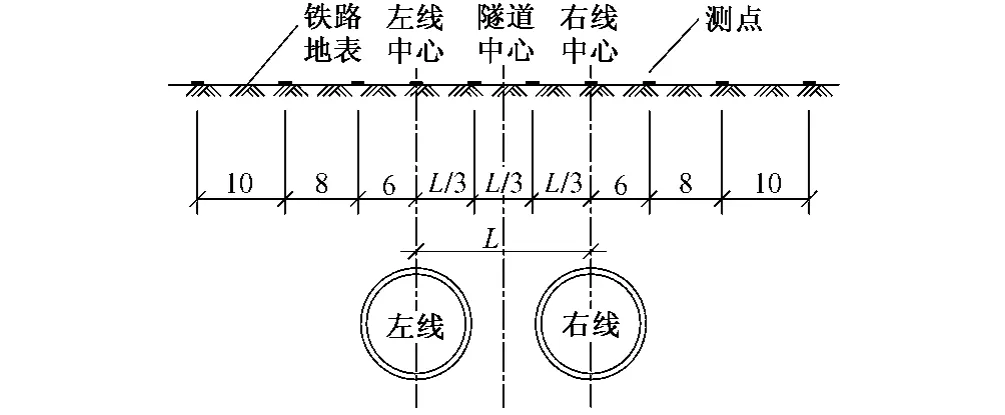
图5 盾构穿越铁路股道段地表横向监测点布设剖面

1)盾构在道路下方推进

图6为盾构(埋深14 m)掘进时，地表纵向观测点某一时刻沉降曲线。右线沉降曲线代表右线盾构通过时，导致的其上方测点的沉降;左线沉降曲线代表左线盾构通过时，导致的其上方测点的沉降。曲线显示，右线盾尾位于96环时，盾构机上方测点沉降速率快，距离开挖断面50～60环处(即40环位置)，沉降基本完成，沉降量约为28 mm。左线盾尾位于96环时，盾构机上方测点沉降速率比右线小，但盾尾后方5～6环范围内沉降速率与右线相当，距离开挖断面60～70环处(即30环位置)，沉降基本完成，沉降量约为10 mm。左线沉降量比右线小得多，仅占右线的36%。盾构通过后，在不同位置测点沉降有所减少，曲线甚至在个别区段发生回弹，为补浆作用引起。需要说明的是，图6为瞬时沉降曲线，左右线的总沉降要大于此值，因为左(右)线推进时对右(左)线上方的测点都会有影响。

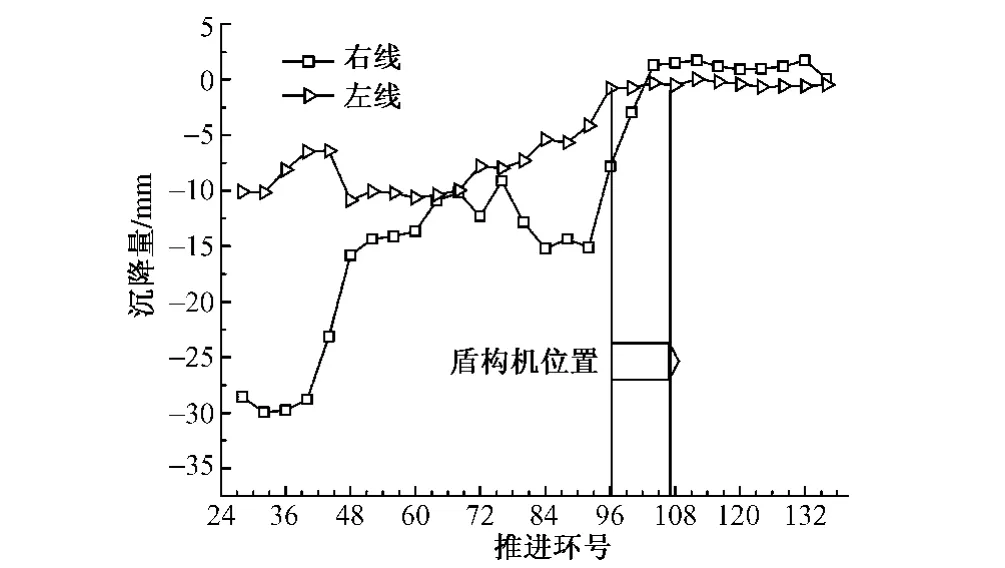
图6 道路地表测点瞬时沉降曲线

2)盾构在铁路下方推进

图7为盾构在铁路下方(埋深为22 m)掘进时，地表测点瞬时沉降曲线，曲线意义与图6类似，但左线测点沉降考虑了右线盾构通过时的影响。铁路段监测断面没有道路段密集，监测断面间距较大，纵向点较少，故采用了拟合曲线表示。曲线显示，左右线盾尾处于794环时，盾尾附近的测点沉降速率较快，距离断面60环处(即735环位置)，沉降基本完成。右线推进导致其上方测点沉降约为14 mm，左右线推进导致左线上方测点总沉降约为13 mm。与道路段相比，补浆对铁路地表测点的沉降影响不明显，沉降曲线没有减小的过程。

图7 铁路地表测点瞬时沉降曲线

3.2 横向沉降

1)盾构在道路下方推进

图8为右线R120横断面沉降曲线。由图可见，右线盾尾脱出时的横断面沉降曲线较盾构机头到达时有明显的整体下移，变化量在5 mm左右，且距盾构中线水平距离较远处与盾构正上方的沉降增量相差不大(即横断面沉降曲线呈现平行下移的趋势)。而最终沉降量则是盾构正上方最大，与盾构水平距离越远，沉降量越小，说明盾构达到前与到达时的扰土范围大，而盾尾拖出后扰土范围减小，主要发生在盾构隧道及其上方位置。从数值上来看，盾尾脱出后又发生的沉降量占最终沉降量的比例较大，为80%左右。

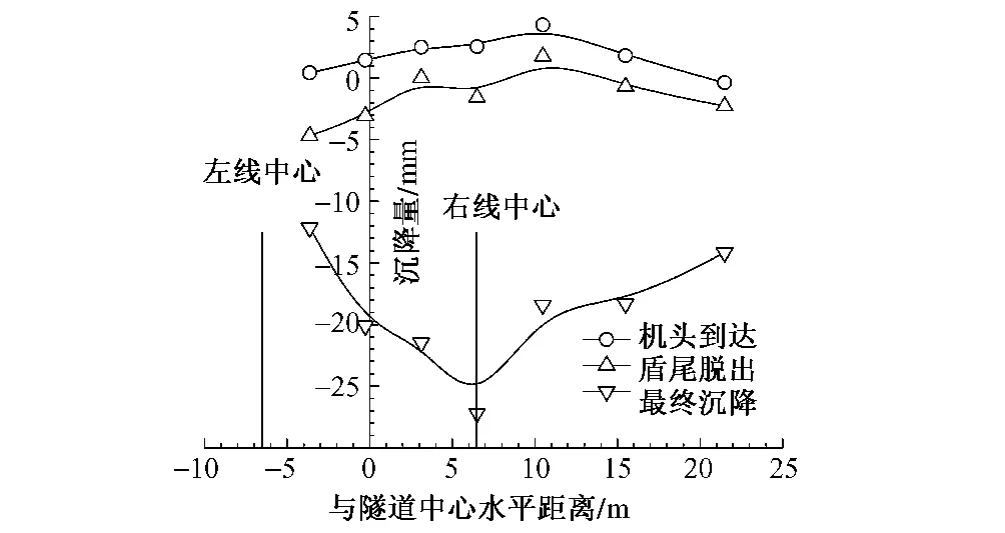
图8 右线R120横断面沉降曲线

图9为左线L120横断面沉降曲线。由图可见，左线横断面沉降规律与右线类似。盾尾脱出后又发生的沉降量也占到最终沉降量的80%左右。由于两条隧道施工相互影响，监测到横向沉降曲线不完全对称，最大值偏向先期施工隧道一侧。

2)盾构在铁路下方推进

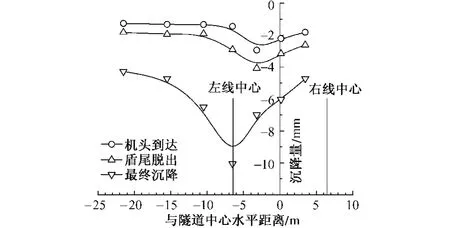
图9 左线L120横断面沉降曲线

图10为右线R690横断面沉降曲线。曲线显示，横断面的总体沉降规律与道路段有相似之处，也能形成规则的沉降槽。右线机头到达和盾尾脱出时间段内，距盾构中心水平距离较远处沉降变化不明显，右线盾构引起的最大沉降为14 mm，盾尾脱出后又发生的沉降量也占到最终沉降量的80%。左线通过后，图形左侧的总沉降量高于右侧，最大总沉降达到20 mm。右线盾构施工引起的沉降远大于左线，占到总沉降的70%。

图10 右线R690横断面沉降曲线

4 Peck 公式［2］反演地层损失率

Peck提出了盾构施工引起地面沉降的估算方法。此法假定地层损失在隧道长度方向上均匀分布，地面沉降的横向分布类似正态分布曲线，如图11所示。

式中，S(x)为沉降量(m);Smax为隧道中心线处的最大沉降量(m);x为距隧道中心线的距离(m);Vl为单位长度地层损失量(m2);i为沉降槽宽度系数 (自隧道中心至沉降曲线反弯点的距离)(m)。

式中，ζ为地层损失率(%);r为隧道外径(m)。

图11 Peck法地表沉降槽曲线

i的计算公式［6］为

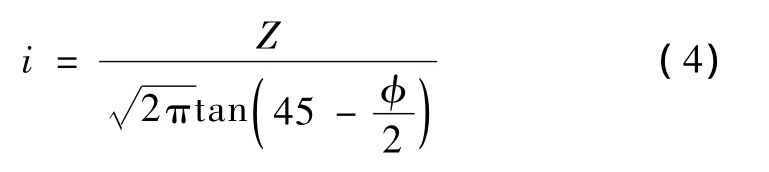
式中，Z为地面至隧道中心深度(m);φ为土的内摩擦角，对于成层土取加权平均值。

Peck公式适用于自由场的工况，对于盾构穿越铁路股道的工况，由于地表有较大的铁路活载，Peck公式不再适用。下面仅对盾构穿越道路段的工况(由于道路荷载较小，可近似按照自由场考虑)，用Peck法反演地层损失率。盾构过道路段埋深在14 m左右，上覆土主要为粉质黏土，内摩擦角φ为17.1°。根据式2～式4，当沉降量为30 mm时，地层损失率为0.471%。Peck沉降曲线与实测曲线对比如图12所示。

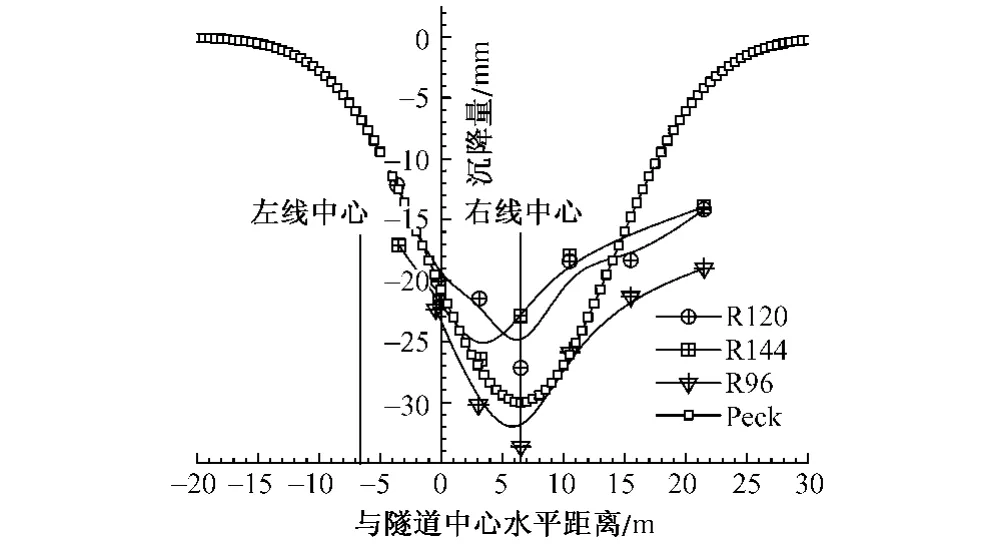
图12 Peck沉降曲线与实测对比

由图12可以看出，测点沉降规律与Peck沉降曲线较吻合，说明Peck法有较好的适用性。R96监测断面最大沉降量为33 mm，超过限值30 mm，可以推算出此测点处的地层损失率为0.518%＞0.471%。经过调整推进参数，减小了R120和R144监测断面处的地层损失率(分别为0.439%和0.424%)，沉降得到了较好的控制，都在30 mm以内。可以看出，若要将沉降控制在30 mm以内，必须保证地层损失率＜0.471%。

5 结论

1)盾构下穿道路段，地表总沉降量基本维持在30 mm以内，左线推进造成的地表最大沉降在10 mm以内(未考虑右线推进的影响)。盾构下穿铁路股道段，右线推进造成的地表最大沉降在14 mm左右，左线通过后导致的地表最大总沉降达到20 mm。左线造成的沉降量较小主要原因是，周围土体得到了右线施工时的注浆加固，另外盾构推进参数的调整对其也有影响。

2)盾构穿越铁路股道段的总沉降小于道路段，与盾构施工参数的调整有关(增大了注浆压力和注浆量)，另外盾构埋深的不同也是一个方面的因素(道路段埋深14 m，铁路段埋深22 m)，埋深越深对地表的影响越小。

3)道路段和铁路段沉降都是在盾构通过约60环(72 m)后基本完成，盾尾脱出后又发生的沉降量占到最终沉降量的80%左右。

4)用Peck公式反演了盾构过道路段的地层损失率，通过计算得出，要将沉降控制在30 mm以内，必须保证地层损失率＜0.471%。

5)盾构过道路段的总体沉降可控制在 +10 mm至-30 mm范围内。盾构过铁路段的最大沉降达到了20 mm，超出了规定的沉降控制范围，变化区域很大，相对差异沉降不显著。由于严密监测与列车运营配合，对地面轨道进行调整，施工期间仍然保证了列车的安全运营。但是必须采取一定的补救措施，如后期的地表加固等，以保证列车长期的顺利运营。

［1］孙玉永，周顺华，宫全美.软土地区盾构掘进引起的深层位移场分布规律［J］.岩石力学与工程学报，2009，28(3):500-506.

［2］PECK R B.Deep excavations and tunneling in soft ground［C］//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City:［s.n.］，1969:225-290.

［3］张海波，殷宗泽，朱俊高.地铁隧道盾构法施工过程中地层变位的三维有限元模拟［J］.岩石力学与工程学报，2005，24(5):755-760.

［4］孙兵，仇文革.双孔盾构隧道地表位移离心机模型试验研究［J］.铁道建筑，2010(2):38-41.

［5］黄金林，苏相利，王贵杰.盾构法隧道施工的横向沉降槽分析［J］.铁道建筑，2008(2):34-37.

［6］WOOI L T，PATHEGAMA G R.Parameters and Considerations in Soft Ground Tunneling［J］.EJGE，2003(8):1-15.