量子化条件与不确定度关系

魏同利，刘家荣

（北方民族大学 基础部，宁夏 银川 750021）

量子化条件与不确定度关系

魏同利，刘家荣

（北方民族大学 基础部，宁夏 银川 750021）

物理学讨论系统某个物理量的本征态时，因为不确定关系的存在，通常会说与其对应的共轭量在这时将没有意义或完全不确定，但这是不符合物理真实的，量子化条件与不确定度关系的同时存在似乎是矛盾的，但我们认为任何物理系统的某个物理量的不确定度在确定条件下是确定的，量子化条件与海森堡不确定关系的共存提示了我们在有些问题中不仅应该考虑本征问题，同时还应该考虑其不确定性，从而得到更加符合物理真实的图像.

量子化条件；本征态；不确定度

1 问题

在量子力学发展的初期，为了解决各种具体的问题，提出了各种各样的量子化条件，如玻尔在他的氢原子理论中提出：环绕原子核作运动的电子的角动量必须为h/2 π的整数倍；粒子在无限深势阱中运动时其动量与势阱尺度的乘积必须为h的整数倍等，事实上，薛定谔正是根据动量与空间，能量与时间的量子化条件得到了薛定谔方程.虽然如此，在量子化条件上仍然有着一些问题需要探讨,在量子化条件存在的同时，海森堡不确定关系也要成立，比如量子化条件p x=n h，同时又有△p△x≥h/2，这是一个矛盾，因为综合以上两式，可以得到一个结论：动量和尺度之间的乘积可以为任何数值，量子化条件将没有任何意义.

根据量子力学的本征态理论，若系统处于某一力学变量的本征态，则每次测量均可观察得到对应于此本征态的本征值，由于海森堡不确定关系，由于该物理量完全确定，则其共轭物理量将完全不确定，这是通常所持的论点.但是我们认为这种看法是不全面的，主要的原因是：自然界不允许我们无限度把一个值确定，而其共轭量却完全不确定.在狄拉克的《量子力学原理》中指出[1]：从物理上看，显然，对q的所有值是等几率的态，或者对p的所有值是等几率的态，实际上都是不能得到的，对第一种情况是因为尺寸的限制，对第二种情况是因为能量的限制.因此p的本征态或是q的本征态，实际上不能完全达到.

由于任何物理学量都有其共轭量，所以上述问题不仅仅存在于正则坐标和正则动量，事实上，所有物理学量的本征态都不可能完全达到，这种情况在物理学研究中广泛的存在，有时甚至比较重要，但这种由于不确定度关系所导致的本征值偏移却很少被提及，本文试图对能量本征值的展宽作初步的探讨.

2 讨论

任何处于能量本征态的系统，都有能量的涨落，或者说能谱存在一定的展宽，这当然是由于不确定关系导致的.当能级有展宽时，意味着系统的能量有一个微小的不确定度，根据关系：△E g△t≥攸/2，能量的共轭量时间也会有微小的不确定度，但是这种关于能量与时间的不确定关系并不是简单的△E越大，△t越小，我们认为：在确定的物理条件下，△E和△t是可以确定的，它们为可观测量.

例如，一束光的能量可以用二次量子化表象表示为：

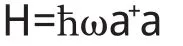
这束光应该有具有n攸ω的能量，光子处于确定的能量本征态，其能量不确定度△E=0，其时间不确定度△t为无穷大，等效为其相干长度无限大.但是在实际的问题中，每种光的相干长度都不是有限大，而且相干长度是可以测量的（等同于时间不确定度可测），所以能量本征值的不确定度也是一个可观测量.这种关于能量的不确定度关系，有望在格林函数的运动方程理论中得到应用[2]，以上面的光子问题为例，假设光子数目为n，能量不确定度为△，根据格林函数的运动方程方法：

可以得到〈〈a,a+〉〉=

根据谱定理有

在格林函数理论中，通常认为该系统光子的能级为攸ω，η为一无穷小的实数，态密度在该能级上为无穷大，在其它位置上为0，但是这并不符合物理真实，在任何情况下，其能量都不会是严格的攸ω，所以η应该在具体的问题当中选取合适的量，如将（1）式中无穷小虚部替换为以不确定度△为大小的虚部，所得到的态密度为，这是以攸ω为中心的洛仑兹分布，可以真实反应此光子系统的物理真实.

能带论认为，能带是由众多的电子能级组成能量区域，考虑到本文所讨论的内容，我们认为能带区域的能级是连续的，简单取模型如下：

考虑少数一维金属电子的行为，假设共一百个能级，均匀分布在-1到1之间，费米能级位于0，哈密顿量可以写为

能级宽度为：△ε=2/100假设能量不确定度为：η=0.1△ε

格林函数的运动方程为：

有：

态密度函数为

任何能量处的占据数密度可以写为：

通过数值计算可以作出占据数密度图：

可以看出，电子占据时会有一定的几率出现于非能级出现处，电子能量态密度连续分布于能带中.

3 结论

任何物理系统在具有确定本征态的同时，还具有确定的不确定度，可以用洛仑兹峰的半宽来描述，它有时是可以测量的（根据光的相干长度来确定其不确定度），它在具体的问题中需要具体来考虑它的大小，根据格林函数理论，它可以有效地得到使用.

参考消息：

〔1〕P.A.M，狄拉克.量子力学原理（第四版）.科学出版社.

〔2〕李正中.固体理论（第二版）.高等教育出版社.

O 413.1

A

1673-260X（2010）07-0012-02