水平井分段压裂产能影响因素研究

唐汝众温庆志苏 建曲占庆

(1.石油工程教育部重点实验室(中国石油大学),北京昌平 102249;2.中国石油大学(华东)石油工程学院,山东东营 257061)

◀油藏与开采▶

水平井分段压裂产能影响因素研究

唐汝众1温庆志2苏 建2曲占庆2

(1.石油工程教育部重点实验室(中国石油大学),北京昌平 102249;2.中国石油大学(华东)石油工程学院,山东东营 257061)

水平井压裂是开发特殊和难动用储量的重要技术手段,在油气田开发过程中得到了越来越广泛的应用。以矩形油藏中压裂水平井为研究对象,在水平井压裂不同裂缝形态的基础上,建立了油藏与裂缝的物理模型和数学模型,并对其进行了差分求解、编程。分析了裂缝长度、数量、间距和不均匀分布等因素对产能的影响,绘制了各个因素取最佳参数时的地层压力分布等高线图。结果表明,裂缝长度和裂缝数量对产能的影响最大,裂缝间距及分布情况对产能的影响相对要弱一些,可以增大裂缝间距以减小彼此之间的干扰作用。这对水平井进行压裂优化设计具有一定的指导作用。

水平井;压裂;数值模拟;裂缝;生产能力;物理模型;数学模型

水平井技术对于开发现有一些特殊和难动用地质储量效果良好[1-3]。对于低渗透油田,往往采用对水平井进行压裂的方法来提高油层产能。采用数值模拟的方法对水平井压裂改造进行研究,并对压裂参数进行优化。进行数值模拟时需要考虑裂缝长度、裂缝数量、裂缝间距和裂缝不均匀分布等因素[4-6]。这些因素对水平井压裂后的产能有很大的影响。

1 物理模型和数学模型的建立

根据所研究油藏的生产特点和水力裂缝的渗流特征,将地层及裂缝看作两个相对独立的系统,两者之间通过地层向裂缝内的窜流量联系起来,以此建立油藏与裂缝的物理模型和数学模型[7]。水平井采用射孔方式完井,只考虑油藏→裂缝→水平井这一过程。

1.1 油藏模型

1.1.1 假设条件

1)油藏内的流动为三维两相流动,油层水平;

2)油藏非均质,其渗透率具有各向异性;

3)地层和流体均微可压缩,且压缩系数保持不变;

4)忽略重力和毛管力影响。

1.1.2 数学模型

渗流方程:

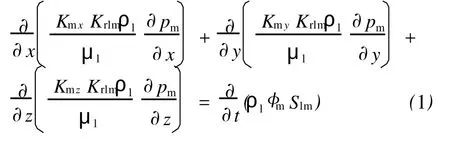
辅助方程:

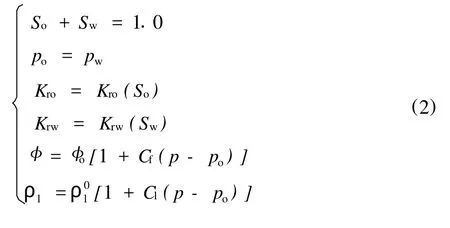
1.2 裂缝模型

由于裂缝厚度很小,在研究水力裂缝时建立两维两相模型,只考虑裂缝面方向上流体的流动,忽略缝宽方向的流动。

1.2.1 假设条件

1)裂缝均质,其渗透率具有各向同性;

2)考虑裂缝导流能力随生产时间的失效;

3)裂缝中流体的流动为达西流动。

1.2.2 裂缝数学模型

渗流方程:

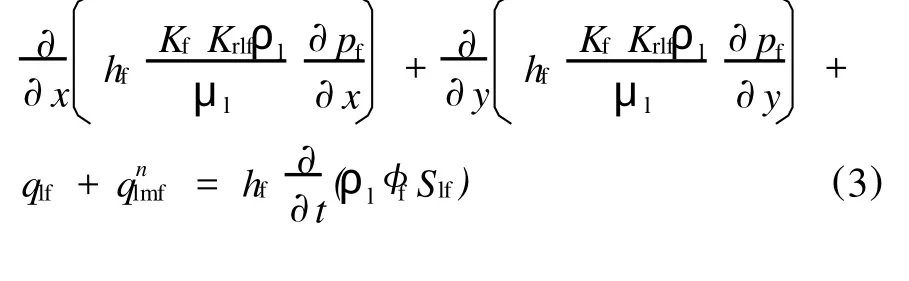
1.3 边界条件

模拟计算时,取油藏外边界为封闭边界。在处理油藏和裂缝的关系时,将其看作两个相对独立的渗流系统。通过裂缝壁面的流量、压力与油藏内渗流流量、压力相等的联立条件建立和求解方程。

1.4 数学模型的求解

对上述数学模型采用有限差分法进行微分方程的离散,将油藏模型和裂缝模型联立后采用IMPES方法求解。为了加快计算速度,采用共轭梯度法来求解[8]方程组,该方法的优点是迭代收敛速度不依赖于迭代因子的选取,收敛速度快。

2 影响压裂水平井产能的因素分析

根据所建立的数值模拟模型,编制了相应的计算机程序,应用该程序对影响压裂水平井产能的各项因素进行了分析。

2.1 裂缝长度的影响

图1为某油井模拟不同裂缝长度时的累计产油量曲线。从图1可看出,随着裂缝长度的增加,产油量也不断增大,但增大到一定程度后增幅变小。考虑到经济及技术因素,对于具体油藏来说,在裂缝数量、储层渗透率及裂缝导流能力等参数一定时,应该存在一个相对最优的裂缝长度。对图1中的井例,裂缝长度从60 m增大到100 m后,产油量及产液量增幅较大;当从100 m增大到140 m时,虽然也有一定增加,但增加幅度变小;从140 m增大到180 m时,则产油量及产液量增幅更小。如果考虑投入产出比,裂缝最佳长度约为140 m。图2为裂缝长140 m时的压力分布等高线。

图1 不同裂缝长度时的累计产油量曲线

图2 裂缝长度为140 m时的压力分布等高线

2.2 裂缝数量的影响

随着压裂工艺技术的不断完善,水平井可以压出多条裂缝。图3为不同裂缝数量的累计产量曲线(假设两裂缝间距为100 m)。从图3可看出:随着裂缝数量的增多,压裂水平井的产油量增大;在相同的生产时间内,当裂缝数量较少时,产油量增加幅度较大;当裂缝数量较多时,产油量增加幅度逐渐减小。这是因为,随着裂缝数量的增加,地层压力下降幅度较大,各条裂缝之间产生的相互干扰也比较严重,使每条裂缝的产量减小,所以随着裂缝数量的增多,产量增加的量越来越小。对一具体油藏,应存在一个最佳的裂缝数量,在保证油藏高效开发的同时,获得最大的经济效益。对于图3中的井例,裂缝数量达到3、4条即可满足要求。图4为3、4条裂缝时的压力分布等高线图。

图3 不同裂缝数量时的累计产油量曲线

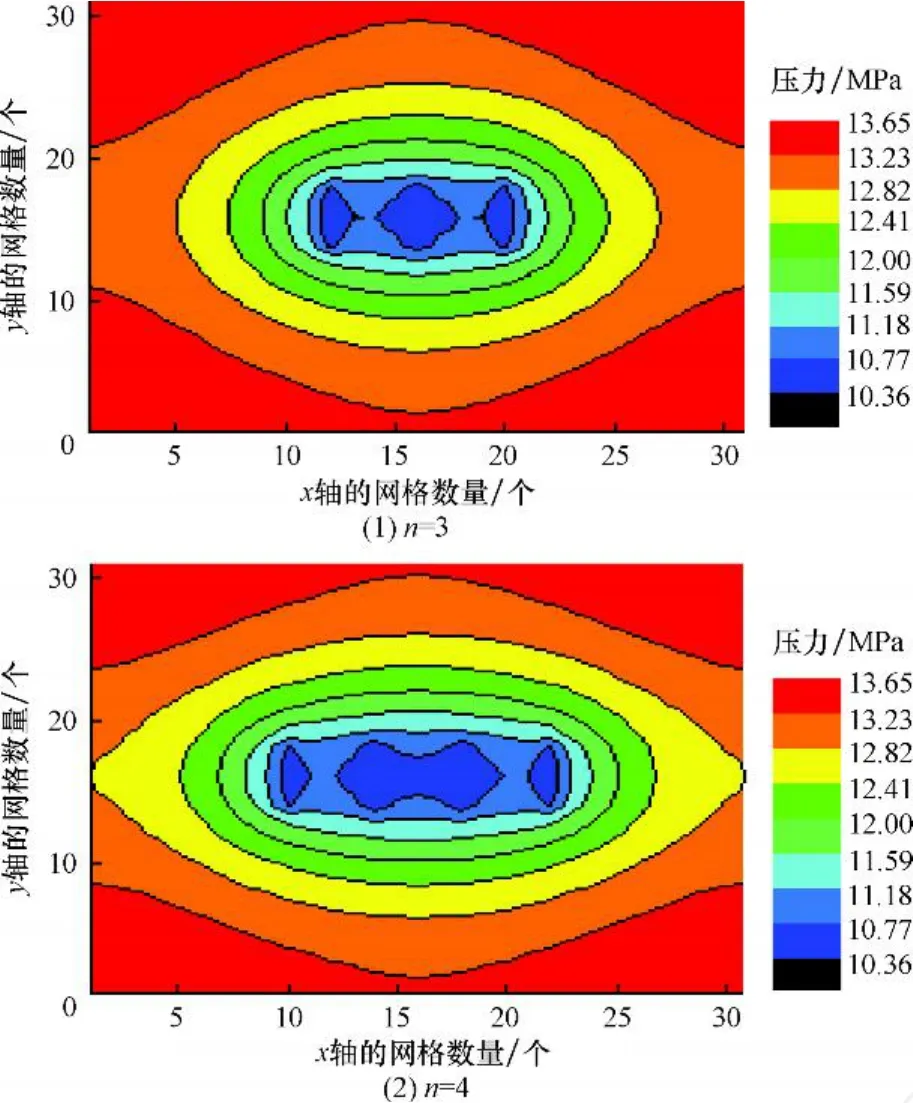
图4 3、4条裂缝时的压力分布等高线

2.3 裂缝间距的影响

为了研究裂缝间距对压裂水平井产量的影响,假设存在两条裂缝,分间距为 100、200、300和400 m等4种情况进行模拟,得到了4种裂缝间距对累计产油量的影响曲线(见图5)。从图5可以看到,当裂缝间距为100 m时,裂缝间存在严重的相互干扰,当裂缝间距为200 m时,干扰作用已经减弱,此时累计产油量已经非常接近。当两裂缝靠近时(如图6所示),相互间的干扰作用就会加剧,在两裂缝间形成一个低压区,而在这个区内所能采出的油是有限的,当达到束缚油饱和度时,就不会有油流向裂缝。

图5 不同裂缝间距时的累计产油量曲线

2.4 非均匀裂缝分布的影响

因地应力分布的不均匀性,可能会导致裂缝相对井筒非对称分布,这里分别取5种分布情况加以分析(见图7),两条相邻裂缝间距为100 m。不同裂缝分布方案时的累计产油量曲线和方案5时的压力分布等高线分别见图8、图9。从图8可以看出,由于裂缝的不均匀分布,产量受到不同程度的影响,当裂缝分布遵循方案5,即成鱼骨状分布时,产油量最大,此时裂缝间的干扰最小,每条裂缝的作用范围最大。

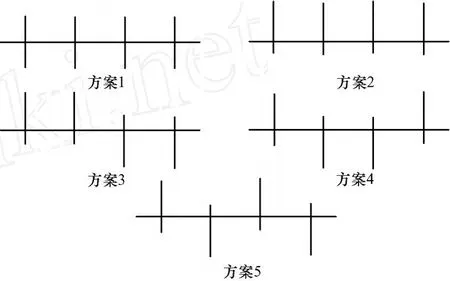
图7 5种不均匀性裂缝分布方案

图8 不同裂缝分布方案时的累计产油量曲线

图9 方案5时的压力分布等高线

3 应用实例

以胜利油田某水平井为例,地层及油井相关参数为:油藏大小600 m×600 m;地层压力18 MPa;产层厚度 20 m;含油饱和度 80%;地层油密度0.745 2 kg/L,黏度1.8 mPa·s,体积系数1.21;地层的渗透率0.05μm2,孔隙度为10%。该井完钻后即进行压裂。

应用编制的软件,结合地层和油井参数,对裂缝参数进行了优化,结果为:裂缝长度140 m,4条裂缝,裂缝间距大于200 m,裂缝采用鱼骨状分布(如图7中的方案5)。该井压裂后日产油量为18 t,获得了很好的增产效果。

4 结论与认识

1)建立了压裂水平井的物理模型和数学模型,并对模型进行了求解,编制了相应的计算机程序,从而实现了应用数值模拟方法分析裂缝形态对水平井压裂后产能影响的目标。

2)对于任何油藏,考虑到压裂后的投入产出问题,都有一个最佳的裂缝参数(裂缝长度、数量、间距和分布)组合,其中裂缝长度和裂缝数量是影响产能的主要参数。

3)为了减少缝间干扰对产能的影响,裂缝间距应大于其相互干扰的有效距离。当裂缝成鱼骨状分布时,裂缝间的干扰作用最弱。

4)结合胜利油田某水平井的压裂实践,表明建立的理论模型准确可靠,可以用来指导水平井压裂设计。

符号说明

Krlm为地层流体相对渗透率,μm2;po、pw分别为地层流体油、水相压力,MPa;μl为地下流体的黏度,mPa·s;Slm为地层流体的饱和度,So为含油饱和度,Sw为含水饱和度;ρl为地下流体的密度,kg/m3; Cf为地层综合压缩系数,MPa-1;pi为原始地层压力,MPa;φm为地层孔隙度;p为目前地层压力, MPa;Cl为流体弹性压缩系数,MPa-1;Kmx、Kmy、Kmz分别为x、y、z方向地层的渗透率,μm2。

[1] 席长丰,江山,马卫国,等.超短半径水力水平井产能计算方法及影响因素分析[J].石油钻探技术,2004,32(1):48-50.

[2] 宁正福,韩树刚,程林松,等.低渗透油气藏压裂水平井产能计算方法[J].石油学报,2002,23(2):68-71.

[3] 刘新华,杨同玉.裂缝性油藏油井流入动态研究[J].石油钻探技术,2002,30(1):59-61.

[4] 魏明臻,王鸿勋,张士诚.水平裂缝参数优化技术研究[J].断块油气田,1999,6(3):36-39.

[5] 高海红,程林松,曲占庆.压裂水平井裂缝参数优化研究[J].西安石油大学学报:自然科学版,2006,21(2):29-32.

[6] 顾岱鸿,田冷.低渗油藏裂缝对水平井产能影响的实验研究[J].断块油气田,2005,12(5):31-33.

[7] 王鸿勋,张士诚.水力压裂设计数值计算方法[M].北京:石油工业出版社,1998:320-324.

[8] Geige S,Matthäl S,Niessner J,et al.Black-oil simulations for three-component,three-phase flow in fractured porous media [R].SPE 107485,2009.

[审稿 吴晓东]

Factors Affecting Productivity of Stage Fractured Horizontal Well

Tang Ruzhong1Wen Qingzhi2Su Jian2Qu Zhanqing2
(1.MOE Key L aboratory ofPetroleum Engineering,China University of Petroleum(Beijing), Changping,Beijing,102249,China;2.College ofPetroleum Engineering,China University ofPetroleum(East China),Dongying,S handong,257061,China)

Fracturing,an important measurement used to develop special or hard-to-recovery reserves, has been used widely in hydrocarbon exploitation.For the purpose of investigating fractured horizontal well in rectangular reservoir,the physical and mathematical model are built and solved numerically.The impact of fracture length,number of fracture,space distance and fracture distribution on productivity are analyzed.Formation pressure distribution contour maps are drawn when all parameters have optimized values.It shows that the length and number of fracture have the main effect on productivity;the space distance and distributions have less effect;and the space distance should be much larger in order to decrease their interference effect.The results provide guidance for optimization of fractured horizontal wells.

horizontal well;fracturing;numerical simulation;fracture;productivity;physical model; mathematical model

book=1,ebook=132

TE357.2+1

A

1001-0890(2010)02-0080-04

2009-03-01;改回日期:2009-09-19

唐汝众(1968—),男,山东寿光人,1990年毕业于西安交通大学,在读博士研究生,高级工程师。

联系方式:18901151898,tang2003@vip.163.com