工程代建合同风险识别与评价＊

杨 枫

(1.中南大学土木建筑学院,湖南长沙410075;2.福建工程学院,福建福州 350007)

工程代建合同风险识别与评价＊

杨 枫1,2

(1.中南大学土木建筑学院,湖南长沙410075;2.福建工程学院,福建福州 350007)

结合福建省代建制管理规定,采用层次分析法(AHP法)进行代建制风险分析与评价,建立项目风险递阶层次结构模型和构造判断矩阵进行计算分析,得到项目建设实施阶段的主要风险因素。研究结果可为委托方及代建单位的风险防范与规避工作提供理论支持。

代建制;层次分析法;风险

代建制作为一种新的投资项目管理体制,在近几年的工程管理实践中取得了令人满意的成绩,但同时也暴露出一些问题,存在着较大的风险,本文结合福建省代建制管理规定,对代建合同的风险进行了分析、评价。

一、代建合同风险识别

代建项目风险根据不同分类方法有不同的范畴,根据风险的性质可以分为政策风险、环境风险、环保风险、经济风险、技术风险、管理风险等,根据风险产生的阶段可以分为项目前期阶段风险、建设实施阶段风险。本文根据《福建省省级投资项目代建制管理办法(试行)》相关规定主要介绍项目在建设实施阶段风险的分析与评价。项目建设实施阶段指从项目初步设计及概算批复后直至项目竣工验收完成,此阶段根据福建省相关代建制的相关管理规定代建单位的项目可能存在的风险主要包括:

(一)勘察设计阶段风险

(1)工程地质条件不确定;(2)设计质量风险;(3)拆迁补偿风险;(4)设计投资控制风险。

(二)施工阶段风险

(1)进度控制风险;(2)投资控制风险;(3)质量控制风险;(4)工程变更风险;(5)代建组织关系协调风险。

(三)竣工阶段风险

(1)工程结算风险;(2)合同风险;(3)主管部门验收风险。

二、代建合同风险分析与评价

合同风险分析的方法有WBS项目分解图法、流程图法、因果分析法、层次分析法(AHP)等。本文采用AHP层次分析法来分析代建项目的风险。

(一)AHP法基本过程

层次分析法可以将无法量化的风险按照大小排出顺序,并把他们彼此区别开来。本文的层次分析法基本步骤如下。

(1)建立递阶层次结构

将复杂的问题分解为不同元素,将这些元素按属性分成若干组,形成不同层次。同一层次的元素作为准则,对下一层次的某些元素起支配作用,同时它又受上一层次元素的支配,形成了一个递阶层次。递阶层次结构模型一般形式见图1。

图1 分层递阶结构模型的一般形式

(2)构造判断矩阵

在单层结构模型中,假定目标元素为A,同与之相连的有关元素B1、B2……、Bn有支配关系,以目标元素A作为准则,通过向决策者询问在原则A下元素的优劣比较,构造一判断矩阵,用Bij表示对于A来说,Bi对Bj相对重要性的数值体现,通常bij取1、2、…,9以及它们的倒数作为标度,其含义如表1所示。构造判断矩阵形式如表2。

表1 标度的含义

表2 判断矩阵

判断矩阵中的元素具有下述性质:

①bij>0;②bij=1/bji;③bii=1;④bij×bjk=bik(传递性)

判断矩阵构建时一般由业内的专家及学术人员构成,专家组的人数应充分合理,太多则意见分散,影响判断矩阵一致性,太少则不能排除个人主管因素干扰。

(3)计算单一准则下元素的相对权重

这一步要解决在准则A下,n个元素B1、B2,…Bn排序权重的计算问题,并进行一致性检验。解特征根问题

式中:B为判断矩阵;λmax为判断矩阵的最大特征根;w为最大特征根所对应的特征向量。

将特征向量w归一化,将所得的特征向量W=[w1,w2,…,wn]T作为本层次B1、B2……,Bn对于目标元素的排序权值。λmax存在且唯一,w可以由正分量组成,除了差一个常数倍数外,w是唯一的。

很明显判断矩阵[B]必须满足下列性质:bij>0;bij=1/ bji;bii=1;bij×bjk=bik(传递性),即要求[B]在一定程度上满足一致性要求。理论上构造出判断矩阵即可计算权重,但是由于判断的复杂性以及人们认识问题的多样性和主观上的片面性、不稳定性,要达到完全一致性是很困难的。为解决这个问题,通常的做法是:事先按照bii=1和bij=1/bji的一致性条件对判断矩阵上三角进行赋值,这样构造的判断矩阵没有经过式bij×bjk=bik的检验,无法保证判断矩阵完全满足一致性条件,因此需要对判断矩阵做进一步的一致性检验。

步骤如下:

①验证判断矩阵是否符合一致性条件的检验步骤归纳如下:

式中n是判断矩阵[B]的维数。

②平均随机一致性指标R I随矩阵的维数而变动其取值如表3～4所示。

③求出判断矩阵[B]的一致性指标CR

一般认为CR≤0.1时,可以认为判断矩阵的一致性是可以接受的。如果CR>0.1,认为判断矩阵不符合一致性要求,需要对该判断矩阵进行重新修正。

表3 判断矩阵R I的取值

(二)递阶层次结构模型

通过对项目项目建设实施阶段进行分析,可建立递阶层次结构模型如图2所示。

图2 项目建设实施阶段递阶层次结构模型

(三)构造判断矩阵并计算分析

通过对福建省部分院校、设计单位、监理单位、施工单位等共18位专家进行调查问卷,并对原始数据进行处理,根据层次分析法判断矩阵构造原则,得出如下递阶层次结构的判断矩阵,并进行了数据分析。

(四)项目建设实施阶段判断矩阵

表4～表8为项目建设实施阶段判断矩阵。

表4 A-B判断矩阵

表5 B1-C判断矩阵

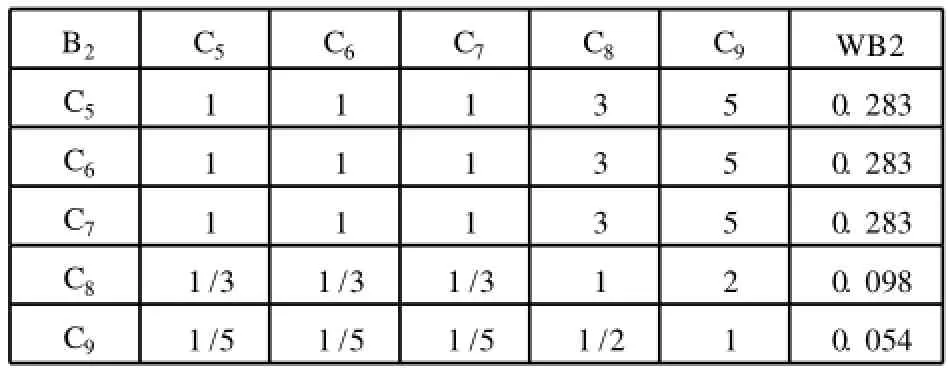
表6 B2-C判断矩阵

表7 B3-C判断矩阵

通过上述判断矩阵的计算,可得出项目建设实施阶段风险因素排序表,如表8所示。

表8 项目建设实施阶段风险因素排序表

对项目建设实施阶段进行一致性检验,各判断矩阵的一致性系数分别为:

A-B判断矩阵,CR=0.081<0.1,一致性判断符合要求,可接受。

B1-C判断矩阵,CR=0.060<0.1,一致性判断符合要求,可接受。

B2-C判断矩阵,CR=0.001<0.1,一致性判断符合要求,可接受。

B3-C判断矩阵,CR=0.033<0.1,一致性判断符合要求,可接受。

风险因素排序矩阵的一致性系数为:CR=0.013<0.1,一致性判断符合要求,可接受。

从表8可以看出,项目进度控制风险、投资控制风险、质量控制风险、项目设计质量风险、工程变更风险是这阶段的主要风险,其所占的比重达到0.78,因此这五个风险是项目建设实施阶段的主要风险。

三、小结

本文对代建项目建设实施阶段风险进行了识别,在识别的基础上对项目风险采用层次分析法(AHP法)进行了分析与评价,建立项目风险递阶层次结构模型,建立判断矩阵并进行计算分析,得到项目建设实施阶段主要风险,为委托方及代建单位双方做好风险防范与规避工作提供理论支持。

[1]陈志华,成虎,周红.代建制的风险分析与控制策略[J].经济问题,2006,(4):26-27.

[2]朱桂荣,邹德欣,单仁亮.项目代建风险及其防范措施研究[J].管理宝鉴,2006,(2):47-48.

[3]翁谦.浅谈我国代建制的风险及控制模式[J].中国工程咨询, 2005,(4):28-29.

[4]张水波,何伯森.工程项目合同双方风险分担问题的探讨[J].天津大学学报,2003,(7):257-261.

[5]李启明,朱冰.工程项目风险分担问题的探讨[J].江苏建筑, 2005,(3):50-52.

[6]李静.基于风险分配的代建合同研究[D].南京:河海大学,2007.

2010-05-17

杨枫(1972-),男,福建宁德人,讲师。