几类广义Feynman-Kac半群的强连续性

梁 青，陈传钟

（海南师范大学 数学与统计学院，海南 海口 571158）

几类广义Feynman-Kac半群的强连续性

梁 青，陈传钟*

（海南师范大学 数学与统计学院，海南 海口 571158）

本文研究几类广义Feynman-Kac半群的强连续性问题.利用文[1]和文[2]中的结果，得到了几类由狄氏型产生的强连续和不强连续广义Feynman-Kac半群的例子.

狄氏型；广义Feynman-Kac半群；强连续

1 引言

设E是一个局部紧的完备可分度量空间，B（E）为E上的σ-代数，m为（E，B（E））上的σ-有限测度，（E，D（E））是L2（E，m）上的正则对称狄氏型，（Xt）t≥0是其联系的马氏过程.有关狄氏型理论的概念及符号见文[3-4].设u∈D（E），～u为u的一个拟连续版本，由狄氏型理论知有如下的Fukushima分解：

此半群是由函数u与马氏过程（Xt）t≥0产生的，称为由函数u产生的广义Feynman-Kac半群.

定理1［1-2］（）t≥0是 L2（E，m）上的强连续半群当且仅当（Qu，D（E）b）下半有界，其中这里（Qu，D（E）b）下半有界是指存在一个常数α＞ 0，使得Qu（f，f）+α（f，f）m≥0，∀f∈D（E）b成立.

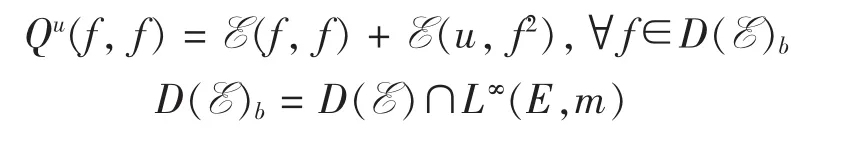
考虑如下形式的狄氏型（E，D（E））：

这里d x为Lebesgue测度，U是Rd上的开集，（aij）1≤i，j≤d的元素aij为定义在 U上的函数，这里的导数是Schwartz分布意义下的导数.杨晓玲在[9]中假设U=｛x∈Rd＜1，xi＞0，1≤ i≤d｝，aij=0，i≠ j；aii＞0，1≤ i≤ d的条件之下，给出了具体的函数例子，并证明由这些函数产生的广义Feynman-Kac半群分别具有强连续和不强连续，这些例子丰富了文[1，2]中内容.本文继续这个问题的研究，去掉（aij）中非对角线上元素为零的假设条件，得到了更多具有强连续性和不强连续的广义Feynman-Kac半群例子.进一步丰富了这类广义Feynman-Kac半群强连续性问题的实例.为了方便我们先给出两个引理：

引理1［1］（）t≥0是 L2（E，m）上的强连续半群当且仅当存在常数0≤ a≤ 1，A≥ 0，使得下面条件成立：

2 主要结果

则当α＞0时，uα（x）∈D（E）.事实上，

由于当α＞0时，2α+1＞-1，

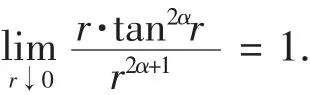
因此

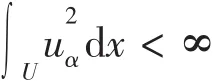
又因为

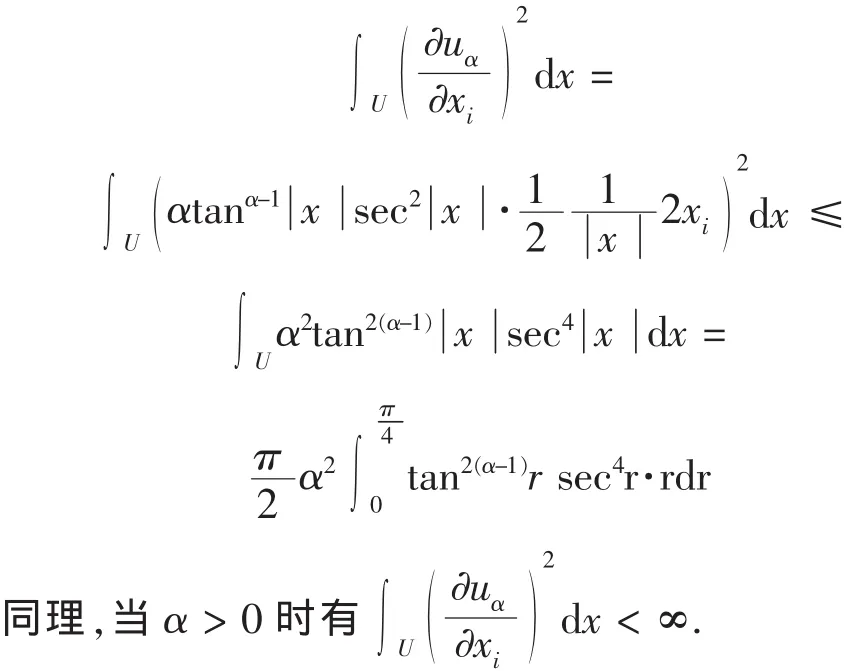
下面给出本文的主要结果，并用不同的方法来证明.

证明一：因为α≥ 1，所以有

因此，由引理2知，（Puαt）t≥0是L2（U，d x）上的强连续半群.证毕.

证明二：设f∈D（E），

考虑式（1）中定义的狄氏型（E，D（E））.令d= 2取

定理4 如果下面条件之一成立：

所以（Qu，D（E）b）非下半有界，再定理 1知（）t≥0不强连续.

（2）同理可证.证毕.

［1］Chen C Z，Sun W.Strong continuity of generalized Feynman-Kac seMigroups：necessary and sufficient conditions[J]. J Func Anal，2006，237：446-456.

［2］Chen C.Z.，Ma Z.M.，Sun W.On Girsanov and Generalized Feynman-Kac Transformations for Symmetric Markov Process[J].World Scientific，2007，10（2）：141-163.

［3］Ma Z M，Röckner M.Introduction to the theory of（Non-symmetric）Dirichlet forms[M].Berlin：springerverlag，1992.

［4］Fukushima M，Oshima Y，Takeda M.Dirichlet Forms and symmetric Markov Processes [M].NeWYork：Walter de Gruyter Berlin，1994.

［5］Ma Z M，Albeverio S.Perturbation of Dirichlet formslower semi-boundedness，closability and forMcores[J].J Funct Anal，1991，99：332-356.

［6］Glover J，Rao M，Šikîc H，et al.Quadratic forms corresponding to the generalized Schrödinger seMigroup[J].J Funct Anal，1994，125：358-378.

［7］Zhang T.Generalized Feynman-Kac seMigroups，associated quadratic forms and asymptotic properties[J].Potential Anal，2001，14：387-408.

［8］Chen Z Q，Zhang T S.Girsanov and Feynman-Kac type transformations for symmetric Markov processes[J].Ann Inst H Poincaïé Probab Statist，2002，38：475-505.

［9］杨晓玲.几类特殊广义Feynman-Kac半群的强连续性分析[D].海口：海南师范大学硕士学位论文，2009.

责任编辑：毕和平

Strong Continuity of Some Classes of Generalized Feynman-Kac SeMigroups

LIANG Qing，CHEN Chuanzhong*
（College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

In this paper，the strong continuity of some classes of generalized Feynman-Kac semigroups is studied，we obtain some examples of Generalized Feynman-Kac Semigroups that may be strongly continuous or not strongly continuous.

Dirichlet form；generalized Feynman-Kac semigroup；strongly continuous

O 211.62

A

1674-4942（2010）02-0134-05

2010-02-17

国家自然科学基金资助项目（10961012）

*通讯作者