关注数学文化 创设教学情境

●叶事一 (教育教学研究院 浙江温州 325000)

1 问题的提出

长期以来，数学教学一贯重视基础知识教学和基本技能训练，要求以多求熟、熟能生巧.这种教学优势明显表现在学生基础知识扎实、数学解题能力强、考试成绩好.然而，我们经常会碰到这样的尴尬：有部分学生在努力学习数学的同时，也渐渐地开始厌烦、冷漠数学，甚至以远离数学为择业标准.

情境教学是新课程倡导的教学模式，一个生动的教学情境可以激活学生的主体意识，调动学生的积极性、主动性和创造性，使学生最大限度地参与探究新知识的活动，让学生在参与中感受成功的兴奋和学习的乐趣，促使学生全身心地投入学习.

在《普通高中数学课程标准(实验)》中，新的课程基本理念提到：“体现数学的文化价值”，并指出，数学课程应适当反映数学的历史、应用和发展趋势，数学对推动社会发展的作用，数学的社会需求，社会发展对数学发展的推动作用，数学科学的思想体系、数学的美学价值、数学家的创新精神.以“体现数学的文化价值”的基本理念为指导思想来创设合理的课堂教学情境对新课程理念下的课堂教学会有怎样的作用?笔者就此结合教学实践谈谈自己的观点，以供参考.

2 关注数学文化视角，创设教学情境的合理性

2.1 “情境教学”的理论基础

先从“情境教学”的理论基础，也就是建构主义学习理论说起.

建构主义学习理论强调“情境”是学习环境的四大要素之一，认为知识不是通过教师传授得到的，而是学习者在一定的情境即社会文化背景下，借助他人的帮助，利用必要的学习资料，通过意义建构的方式获得的.这里包含着2层意义：其一，建构性教学为学生提供的信息是多样化的，强调信息的情境化，教师创设的教学情境必须是真实的、具体的，要帮助学生利用各种有力的工具来促进学生自己建构对知识的理解;其二，建构主义强调学生是积极主动的知识建构者，要求学生在一种复杂而真实的情境中，在教师适度的帮助下，采取富有个性的认识加工策略，形成自己对知识的独立理解.

2.2 数学文化为教学情境的创设扩展了资源

数学的发展与人类文明的发展是同步的，已有5 000多年的发展史，现在数学已经渗透到社会的各个领域中.因此，所蕴涵的数学课程资源是无比丰富的.它或者是一段使人“知兴衰”的数学史、“知得失”的数学家生平介绍和引人入胜的数学趣闻;或者是某个发人深思的数学思想、精彩美妙的数学方法和让人着迷的数学命题;或者是展现数学在科学技术、政治经济、文学艺术以及社会现实生活中那些漂亮的应用……依照“基础性、普及性、发展性”原则，我们可以从数学文化视角出发，利用数学科学价值(如数学名题、科学中的数学)、人文价值(如数学家生平、中国数学史中的优秀成果)、应用价值(如身边的数学、其他学科中的数学)与美学价值(如数学美的解读、艺术中的数学)等维度为课堂创设合理、生动地教学情境，从而将数学文化渗透到课堂中去.

3 数学文化视角下教学情境的特征

数学文化视角是一个独特的视角，在这个视角下的数学不仅仅是一些事实、公式、规则、规律、定理、定律，而且，数学还包括丰富的日常生活、社会生活、生产劳动、政治决策、工业管理……以及各类探索活动的来源与应用.在这些来源与应用活动中，数学是可错的、相对的、猜测的、整体的、类型多样的……由此可见，数学文化视角下的教学情境，除了依照问题设计规律及教育教学目的、数学学科特点，具有教学的必要因素与必要形式外，还应有其自己的特征：

第一，有效性.任何情境的创设都旨在为“有效教学”服务，主要有3层含义：(1)有效果：指结果与预期吻合程度的评价;(2)有效率：教学效果和教学投入的比值;(3)有效益：指教学活动的收益、教学活动价值的实现.

第二，可及性.跳一跳，够得到.情境的创设要符合学生的一般认识规律、身心发展规律，包括学生的知识经验、能力水平、学习习惯、生活经历及环境，个性、爱好及基本心理状况等.

第三，趣味性.能激发学生兴趣，调动学生的积极性、主动性，使学生最大限度地参与到探究活动中来，让学生在参与中感受成功的兴奋和学习的乐趣，促使学生全身心地投入学习.

第四，应用性.要让学生切实地感受到数学的应用价值，培养学生的应用意识，使学生感受到“数学就在身边”，数学可使人们更加合理地做出判断和选择，帮助学生认识到：数学是有用的.

第五，人文性.能开阔学生视野，探寻数学发展的历史轨迹，增强学生的民族自豪感，提高文化素养，养成说理、批判、质疑等理性思维的习惯和锲而不舍的追求真理精神.

4 数学文化视角下教学情境的创设途径

4.1 通过数学名题创设教学情境

例如在执教“数列的递推公式(数列复习课第1课时)”时，可从谢宾斯基三角形出发，引导学生探究递推公式.

(1)介绍数学的历史与文化.

上世纪初，波兰的数学家谢宾斯基想要找到一种图形：当它的面积无限减小时，它的周长却无限增大(用几何画板进行迭代演示).

(2)数一数.

将上迷迭代过程逐一展示(如图1)，让学生数一数在每个图形中浅色三角形的个数依次为多少?引出该等比数列的递推式及通项公式.

图1

(3)再数一数.

每个图形中浅色、深色三角形的总个数依次为多少?学生容易得出前3项为1，4，13.

(4)探究：第4项是多少(从特殊到一般，引出递推公式)?

图2

方法1 几何方法.从第2个图像起，每个图像都可以看成由前一个图像的3份缩影加上中间一个深色三角形(如图2)，因此bn=3bn-1+1(n≥2).

方法2 代数法.从前3项的数值1，4，13中可以猜想：bn=3bn-1(n≥2)，于是

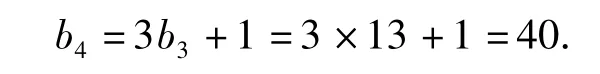
方法3 代数法.由 b2-b1=3，b3-b2=9，b4-b3=27，可猜想 bn-bn-1=3n-1(n≥2)，因此

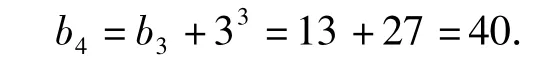
图3

方法4 几何法.从第2个图像起，每一个图像是在前一个图像的基础上将每个浅色三角形中位线构成的三角形变为深色，这样如图3所示圈内1个三角形就变成4个三角形，增加了3个三角形.在第n-1图形中，浅色三角形的个数为3n-2，于是 bn=bn-1+3n-2×3，即 bn=bn-1+3n-1(n≥2).

谢宾斯基三角形是教科书中的一个例题，只给出了数列前面几项，但作了以上的深度挖掘，从不同的视角去引导学生观察、分析谢宾斯基三角形的变化，并从中探究数列的递推公式，加上数学历史与文化的渗透，传递自然、连贯贴切、气氛融洽，凸显了学生的主体地位.

4.2 通过数学应用创设教学情境

数学课程标准指出：要培养学生“用数学的眼光认识所生活的环境与生活”，学会“数学地思考”.从身边的数学应用于其他学科的成果中创设情境，正是实施新课程标准的有效策略之一.

又譬如，教师在执教“指数函数”时，可以从一则新闻报道引入：1994年8月，美国考古学家在阿拉斯加州一处地窖中发现一具女童尸体，在无史料记载可考证的情况下，考古学家却能测定出这名女童大约死于公元1200年，你知道考古学是怎样测量女尸的年代的吗?其实，这是根据人体中含有的一种放射性无素“碳-14”的衰变速度(每年人体内有的“碳-14”衰变成“氮-14”)与尸体内的“碳-14”的含量进行推算的.

同时在教学中，教师也可以向学生介绍现实生活中的数学信息，如数学在CT、核磁共振、高清晰度彩电、飞机设计、天气预报等重要技术中发挥着核心作用，介绍数学知识和数学思想方法在其他科学和现代生活中的应用，展示数学与其他自然科学、交叉科学之间的联系，使学生感受到数学的应用价值和社会需要.以纠正其观念中数学最主要的作用是为了计算，数学学习的最终目的是为了考试等错误认识，培养学生的创新欲望，展示数学文化的应用价值.

4.3 通过数学悖论、趣题创设教学情境

例如，在讲授“直线的倾斜角与斜率”内容时，可以考虑一个著名的几何学悖论——“魔术师的地毯”来创设教学情境，让学生体会推理严谨的必要性.魔术大师秋先生拿了一块长和宽都是13 m的地毯去找地毯匠敬师傅，要求把这块正方形地毯改制成宽8 m，长21 m的矩形地毯.敬师傅说：“不可能的，你的地毯面积是169 m2，而宽为8 m，长21 m的地毯面积只有168 m2.除非裁去1 m2，否则没法改.”秋先生拿出事先画好的一张设计图纸，对敬师傅说：“你先照图4的尺寸把地毯裁成4块，再照图5的样子缝好就行了.魔术大师是从来不会出错的，你只管放心做吧.”敬师傅照着做好之后一量.果然是宽8 m，长21 m的矩形.魔术师拿着改好的地毯得意洋洋地走了，而敬师傅还在那里纳闷呢，那1 m2的地毯哪里去了?你能用学过的知识帮助敬师傅找出原因吗?

图4

图5

数学悖论指一切与人们直觉和日常经验相矛盾的数学结论.它以“趣味数学”闻名于世，具有较强的游戏色彩，容易吸引学生的注意力和兴趣，促使他们去发现错误、研究缺陷，有助于激发他们数学学习的兴趣和锻炼数学的思维能力.

4.4 通过数学故事、人物创设教学情境

例如，湖南版新课程数学教材在每一章节的篇头用一首诗来概括本章的主要精神，为本章内容的学习营造一种数学文化的氛围.《数列》的篇头诗是这样的：“玉兔子孙世代传，棋盘麦塔上摩天，坛坛罐罐求堆垛，步步为营算连环”.这首短短的诗介绍了历史上与数学有关的4个故事：“玉兔子孙”讲的是斐波那契数列(Fibonacci兔子数列);“棋盘麦塔”讲的是古印度国际象棋发明者向国王要奖赏的故事：他所要奖赏的麦子总数是1+2+22+23+…+263，这样多的麦子堆成的“麦塔”可以从地球一直堆到太阳上去，所以说“棋盘麦塔上摩天”一点也不夸张!堆垛和连环都是中国古代的数列问题.教材中很多章节都蕴涵着丰富的数学文化底蕴.在平时的教学中，教师应充分挖掘教材，让学生感悟数学文化，提升数学课堂的亲和力.

又譬如在教学“解析几何”前，要求学生课外阅读《解析几何的诞生》，并上网搜索数学家笛卡儿、费马的资料，上课时教师花几分时间让学生谈谈体会.学生都被笛卡儿的刻苦学习、大胆设想、要向“世界这本大书”讨教的学习精神所感动;再如阅读材料《当代中国杰出数学家——吴文俊》，可以让学生在课上朗读，虽然花了几分时间，但是可以让学生了解数学先辈们刻苦钻研的作风、富有启发性的治学经验和崇高的思想品德.他们是数学教学中激发学习兴趣、激励学习积极性、学习科学方法和弘扬民族精神的极其生动的思想养料.

4.5 通过数学美创设教学情境

譬如在复习“几何概型的应用”时，教师可通过“蒲丰投针问题”介绍圆周率与几何概型，体现数学的奇异美：π=3.1 415 926…已成为家喻户晓的数学常识，但π的值还可以利用概率知识得到可能就鲜为人知了.请看下面的试验：

图6

图7

如图6，平面上画着一些平行线，它们之间的距离都是n.向此平面随意投一长度为m(m＜n)的针，求此针与任一平行线相交的概率.

分析以x表示针的中点到最近一条平行线的距离，以α表示针与平行线的交角.样本空间

在概率教学中，介绍利用概率知识计算圆周率的方法，不仅可以使学生体验到数学的奇异美，同时还会使学生感受到数学的进展是脚踏实地的，不像神话、传说那样虚无飘渺，但数学的进展却又使一切神话黯然失色!

又如，在讲解习题“设函数

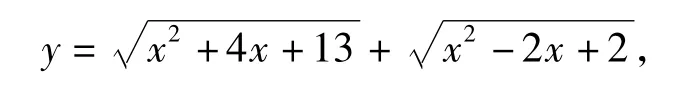
求函数的最小值”时，本题看上去是一道纯代数题，但经构造可化数为形，轻而易举解决，让学生感受到数形结合之美妙!

先变形为

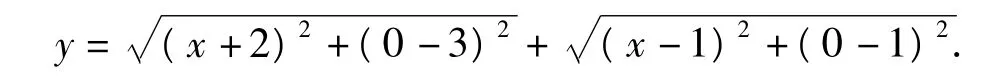
由平面上两点间距离公式可知，本题实际上可转化为求 x轴上一点(x，0)到(-2，3)和(1，1)两点距离和的最小值，即“两点间线段最短”.本题起关键作用的是化数为形，然后是对称点的作用.一个思想、一个原理，构成一幅精美的科学图画.科学之美油然而生.欣赏数学中的美，体味数学的统一美、和谐美、简洁美、对称美、奇异美等，可大大改变目前数学课堂枯燥乏味的现状，让学生的情趣盎然，体现数学文化的美学价值.

关注数学文化，创设课堂教学情境，提升学生学习文化品质，营造和谐、向上的课堂氛围，这样才能挖掘数学博大精深，探索创新之美.因为知识不是独立的点，而是连成一片的网，是推理演绎着的流水，流向更深邃的远方.

［1］ 雷玲.中学数学名师教学艺术［M］.上海：华东师范大学出版社，2008.

［2］ 吴丽娟.结合概率史实，彰显数学文化［J］.数学教学研究，2009(2)：8-11.