激励机制对学生成绩的影响
张大彤,鞠文华
1.2.北京大学,北京 100871
激励机制对学生成绩的影响
张大彤1,鞠文华2
1.2.北京大学,北京 100871
作者抓住学生成绩这个各方面最关心的问题,与马太效应相联系,结合所学的知识,潜心分析与探究,得出合理的分析结论,为今后高校在制定对学生相关奖励与激励政策上提供了可操作性较强的依据。
激励机制;学生成绩;马太效应
一、引言
在进入大学校园以后,成绩无疑是每个学生最关心的问题。通过研究,学生现在的学习成绩可以被先前的成绩或者学习基础、学习背景所影响。但是这种影响并不是决定性的,因为样本会经历很多变革,比如各种奖励、支持及许多形式的自我价值的肯定。大学学习期间,那些学习优秀的学生受到了正向的激励,对自己的学习与前途充满了信心,就会倾向于有更高的成就动机,就会更加努力的提高自己,从而使得自己更加进步。
学校在多年从事奖励工作中已经制定了多项奖励、鼓励等政策和制度,积累了丰富的经验,掌握了大量的情况。但是,对于在校的学生来说,是怎样看待学校目前实行的奖励机制呢?这些现有的奖励机制对学生的成绩又有怎样的影响呢?基于这些问题我们设计出了一个问卷,通过对学生相关成绩背景和激励获得情况与激励反馈情况的调查,来反映学生们对学校各项激励活动的内心想法和对于学习成绩实际的影响程度,进而为今后学校在制定对学生相关奖励与激励政策上提供可操作性较强的参考依据。
二、成绩背景因素、激励因素量化与配比权重的模型
(一)基本假设
假设,每个人m每一年同时拥有两个分数:成绩背景分数I、激励分数S,并通过这两个分数线性叠加出一个总分数T:Tm=a*Im+(1-a)*Sm
其中:Tm:激励总分数,a:权重系数,Im:成绩背景分数,Sm:激励分数
每个学年所有人m都可以用量表和计算方法换算出一个总分T,所有样本的总分数排名应该与这些人下一个学年在总样本中的GPA实际排名十分接近。
(二)成绩背景分数

其中rank1为第m个同学第一学年成绩相对排名的百分比。在我们看来,大学生在第一年入学,对于大学情况了解不多,也没有获得奖学金的机会(奖学金一般是在大二开学时根据大一的成绩进行评选),深入与教授谈话获得激励的机会也不是很多。所以,把入学第一年的成绩作为该学生的成绩背景分数代入计算是合理的。
(三)激励分数

其中Gmi为第m个同学对第i种激励的百分制评分,而且这个评分是针对该刺激类型的满度刺激,也就是获得物理上最大的刺激量时这位学生对它的反馈程度。为了一致性考虑,在后期编程中将每个同学的各项评分都除去一个特殊的系数,使得每个人的评分之和为100。
Qmi为该同学获得激励的数量,fi(Q)是利用心理学中的费西纳定律得到的分数换算函数。下面详细讨论这个换算函数。韦伯(Ernst Weber)指出差别阈限是特定刺激的一个常分数。后来为了描述连续意义上心理量与物理量的关系,德国物理学家费希纳(1801-1887)在韦伯研究的基础上,于1860年提出了一个假定:把最小可觉差作为感觉量的单位,即每增加一个差别阈限,心理量增加一个单位,这样可推导出如下公式:S=k ln I+C(S为感觉量、K为常数、I为物理量,C是积分常数)通式:S=k log I。其含义是感觉量与物理量的对数值成正比。费西纳定律告诉我们,感觉量与物理刺激量是成对数关系的。但是这个公式中很多量尽管是常数,但是都是需要我们调查分析的。为了使最终的函数满足对数函数的形式,并且分数可以从0取值到1,我们假定在满度刺激Q1的时候,受到的激励换算函数值为1,而在绝对阈限Q2处感受的激励换算函数为0,小于绝对阈限的刺激量均不会对学生造成任何激励,因此同样为0。

其中A、B均为常数,通过两个边值进行定解。最后得到:

另外,对于一些以时间多少衡量的刺激,没有用该公式衡量,因为时间的满度刺激量很难估计,不像奖学金最大金额那样明确而且客观。因此,对于这样的刺激,比如参加演出的次数、与教授交流的时间等,我们在选项中采取了非线性的设计,尽量满足费西纳定律所要求的形式。于是这部分的换算函数就可以简单的按照每一个选项0、1/ 3、2/3、1评分。
(四)总分的叠加
在叠加总成绩的时候,我们假设成绩背景分数力与激励是线性叠加的。于是出现了一个权重系数a。这个权重系数是成绩背景分数的权重,所以激励分数的权重就应当是1-a。为了得到这个系数a,我们采取了从0步进到1,考察最终总分排名与第二年实际排名的拟合程度,最终找到使方差最小的系数a。
三、问卷设计与数据分析
基于这些假设的指导,我们设计出了一份关于《激励机制对于学生作用》的调查问卷,调查样本140份,收回有效样本70份,并用C语言编写程序进行分析,最终得到了一些比较满意的结果。
我们首先在量表中设计了调查表格,里面包含各个学期该学生的综合成绩的排名百分比,这些信息将作为成绩背景因素或最终拟合的参量加以分析。
在问卷的第二部分,我们列举了10种主要的激励,例如:奖学金、学科竞赛、助学金、科研机会、教授面谈、学术竞赛、讲座、体育文艺比赛和演出等。统计所有学生获得这些激励的情况,数量多少或时间长短。最后,我们让同学们想象自己获得了第i项激励的最大数额的激励,比如奖学金10000元或者数学竞赛特等奖,自己受到激励的程度,属于激励之间孰重孰轻的调查。
(一)编程与分析
我们利用C语言和origin 8.0对数据进行了细致的处理和分析,并画出了拟合方差随权重系数a的关系图[见方差与权重系数a的关系图(一),其中将a=0.8到a=1之间的图像放大就成为方差与权重系数a的关系图(二)]。
编程的主要过程是:
A、对储存在文件中的数据文本执行读入操作。
B、在文本文件中设定各个刺激的绝对阈限与满度刺激值,并读入程序。
C、执行分数换算函数,根据假设中的公式将问卷中的各个量代入,其中每一学年的成绩利用该学年的两学期排名取得平均值,最终得到每一个学生的成绩背景分数与激励分数。
D、对a进行步进,从0开始,步长为0.0001一直步进到1。a每次取值都对应一种总分换算办法,对于该办法进行总分排名。但是排名后得到的是样本间(70人)的排名而非实际预测的在年级中(百分制)的排名。所以我们利用统计学的方法对这个相对排名进行估计,具体的估计办法是:对原来的70人第一年在年级中的排名求和得到Σ1;再对1到70求和得到Σ2=Σ70i=1i。我们假定第二年这70人在年级中的排名和不变。设ε=(Σ1-2)/70则每一个人的预测排名为该学生在样本间的排名加上ε。有了预测排名,我们还统计到了第二年的实际排名,于是每一个a就会对应一个排名的方差。对a与排名拟合方差列表或者画图查找最小值,发现a的区间为0.880300到0.882900之间。在这个区间内的预测标准偏差为9.97,预测排名和实际排名拟合相关系数为0.905454,趋势预测准确率为71.43%(预测排名上升实际确实上升了,预测下降实际确实下降了)
E、取a为0.881600代入计算,将激励值代成第二年的激励分数,对下一个学年进行预测(预测表格见表一),这个预测将会与下一年的真实排名进行比较来修正我们的公式。
F、对造成大方差的样本进行误差分析。
(二)研究的结论与合理化建议
1.拟合结果.Tm=0.8816*Im+0.1184*Sm
2.对于结果的分析与合理化建议。对于学生们来说,大学期间的综合成绩受成绩背景因素的影响相对较大 (占到88%)。这种成绩背景因素比较全面反映了学生受到激励机制影响之前的个人基础状况。
通过研究,我们发现,尽管激励的权重也就是12%左右的程度,看上去不能够对学生的排名产生决定性的影响。但是,对于排名接近的几位同学来讲,激励对于他们排名次序的影响就很大了。因为这些同学成绩背景因素相差无几,尽管这一部分权重很大,占到了近九成,可是相对差值也不过是零点几的大小。这时候,一旦一个同学得到了一次可观的激励,那么对于这几个人的小群体来说,将会是决定性的因素。所以作为掌握这些激励发放的负责人一定要公平公正,否则将会造成不平等的竞争,后果不止是资源分配的不公平,更重要的是被激励的同学将会在后面得到越来越多的激励。用数学的语言就是Qmi与Sm正相关,排名(总分)越好,就越容易获得更多的激励 Qmi,于是将会有更大的 ΣNi=1Gmi*fi(Qmi),最后将会获得更高的总分,排名就会继续上升。如此循环下去,刚开始成绩相差无几的几个人到后来就被拉开了差距,马太效应就这样产生了。所以尽管激励因素并不是影响学生成绩的最重要因素,然而如果这种激励方法运用不当,导致学生产生的心理压力不会是微小的,相反,这种影响会随着马太效应而得到放大。
作为学生的我们也同样能从这个研究中得到几条建议。首先当然是努力最重要。除此之外,在激励的数量Qmi上我们应该放飞自己,去争取更多的激励,去争取更多的正向的推力;在激励的反馈分数Gmi上,我们要对于已经获得的激励感到骄傲、感到自豪,让这份激励充分发挥作用,以获取更高的分数。
由于同学们配合度的原因,有效样本仍显得数量不足,或多或少地影响了推算结果的误差,需在今后不断加以完善。但从对数据进行的可信度判断及推断结果上看:分析模型所反映的基本趋势是正确的;所用的程序是可以拓展到更大样本分析与应用中;本次研究的应用成果在一定程度上是为学校完善相关奖励机制与制定相关奖励政策提出的一种切实可行的分析、监测问题的方法。
(三)误差分析

编号ID 第一学年排名 第二学年排名 预计第二年排名9 40 25 44 19 85 85 69 29 40 25 45 37 50 35 51 39 40 5 43 42 30 20 35 50 10 25 8 59 60 30 57 64 55 35 54
调查问卷显示:上表列出的一些样本造成了比较大的方差贡献。趋势图显示:这些样本的名次起伏比较大,也就是说按照模型计算结果推断这些同学应受到很大的激励,而实际结果由于受到各方面因素影响却没有得到预定的结果,即进步许多名。基于上述情况,调查中我们又重新对这些样本的真实性进行了核实,也就是抽选一些排名起伏较大的部分同学(例如大一年级比大二年级名次前进了57名的同学、第二学年比第一学年名次前进了66名的同学)进行了访谈。提出例如“成绩上升的原因是什么?”的问题,要求同学们回答。
第一年发挥是否正常?选课的原因?不适应?适应又代表什么呢(什么方面的适应)?
你认为成绩上升是否是偶然情况?今后是否还有上升的空间?
你觉得你成绩上升背后有什么动力?来自哪里?
你觉得促使你成绩上升的最主要的原因是什么?
访谈结果表明了样本数据的真实可靠性。因此我们认为:抽样调查是遵循随机原则,离群值的出现也是正常的,从拟合的整体趋势上看是一致的。
深入分析误差来源大致受以下因素影响:第一年的成绩也许对于某些人来讲不能作为一个很好的个人基础状况的评价指标,也许有些人还不太适应大学的考试体系,也许有的同学由于复习的方向恰好是重点而超常发挥(在后面的个别情况的访谈中我们对于这些问题予以了澄清与解释)。这样说来,9.97的标准差应该是可以接受的,后续成绩单的公布可以继续验证和修正我们的公式。
四、预测数据和图表
(一)预测下一年的排名

ID 预测排名 ID 预测排名 ID 预测排名1 41 25 53 49 12 2 49 26 24 50 8 3 58 27 18 51 57 4 14 28 31 52 10 5 67 29 45 53 7 6 65 30 26 54 68 7 61 31 36 55 69 8 71 32 21 56 38 9 43 33 4 57 25 10 52 34 27 58 16 11 23 35 20 59 54 12 33 36 19 60 28 13 9 37 51 61 64 14 50 38 60 62 48 15 32 39 42 63 22 16 62 40 3 64 56 17 44 41 11 65 6 18 55 42 35 66 17 19 70 43 59 67 30 20 46 44 2 68 29 21 39 45 63 69 5 22 34 46 15 70 13 23 37 47 47 24 66 48 40
(二)系数a—预测与实际排名方差的关系图

(三)样本量分析报告
1.抽样设计。根据要求抽样的目标总体为**大学本科生,抽样总体则是包括了对激励机制认同和不认同以及无所谓的三部分学生。因此抽样总体小于目标总体。考虑到样本框信息的不足和调查资源限制等因素,经考虑决定采取随机抽样方法,并以认同激励机制同学占全部学生的认同率作为抽样标志确定样本量。
2.样本量确定。假定抽样推断估计值的允许误差范围为± 0.1,置信度为95%(z=1.96),设计总体为140人。另外由于没有关于认同率的具体信息,因此方差取最大,即P=0.5。样本量计算如下:
①初始样本量并修正
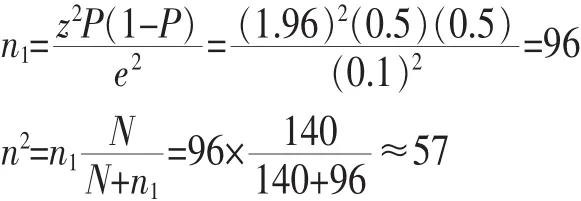
②设计效应调整样本量(deff=1.8):
最终样本量(人)n3=deff*n2=2×57≈103(人)
3.抽样误差。经计算,样本均值为70%(对激励机制的认同率),根据不重复性抽样平均误差分布服从正态分布的假定(95%的把握程度即t=1.96),抽样平均误差和抽样允许误差的公式计算如下:
①抽样平均误差

式中:P为认同率,n为样本数,N为总体单位数。
②抽样极限误差
Δ=t·μp=1.96×0.085=16.7%
4.假设检验。抽取样本中的10%重新放回试验来说明对总体推断的假设是否成立。
①双侧检验假设
原假设:H0∶X=70% 备择假设:H0∶X≠70%
②检验统计量计算
检验统计量计算为:

③做出决策
[1]Charles G.Morris,Albert A.Maisto.张继明,王蕾,童永胜译.心理学导论(第12版)[M].北京:北京大学出版社,2007.
[2](美)理查德(Richard J.G)等.心理学与生活[M].北京:北京大学出版社,2003
.
责任编辑:周晓华 陈 岩
The Influence of Encourage Mechanism to the Student Achievement
ZHANG Da-tong1,JU Wen-hua2
(1.2.Peking University,Beijing 100871)
The authors catch the problem of the student achievement,with Matthew Effect and their knowledge and analysis and research,finally draw a logical conclusion and provide strong operational basis for the institutions of higher education in their future formulation of relevant policies and incentive to motivate students.
encourage mechanism;student achievement;Matthew Effect

book=56,ebook=60
G642.47
A
1008-9055(2010)03-0056-04
2010-03-20
1.张大彤(1989—),男,汉族,天津市人,北京大学物理学院学生。研究方向:心理测量,行为心理学。
2.鞠文华(1989—),女,汉族,山东省东营市人,北京大学物理学院学生。研究方向:心理测量,行为心理学。

