关于电场叠加原理的进一步讨论

■丁同合

电场叠加原理在物理学中是一个比较重要的原理，也是一个比较难理解的原理，特别是对初学者学习起来更是困难。为了帮助人们更好地学习和掌握该原理，下面在该原理的基础上作进一步探讨。

电场叠加原理指出：一组点电荷所激发的电场在任一点的场强等于各个点电荷“单独存在”时所激发的电场在该点的场强的矢量和。原理中说的是点电荷的场强叠加，那么对于非点电荷（即带电导体和带电导体组）是否也适用呢？

要想探讨场强叠加原理是否适用于导体，首先必须对点电荷这个概念要有正确的理解。点电荷这个概念是人们为了研究问题的方便而提出的，是一个理想模型，一个带电体能否被视为点电荷应视具体情况而定，带电体在某些情况下可以被视为点电荷，而在某些情况下又可能不能被视为点电荷，所以说点电荷的概念具有相对意义，那么一个带电导体能否被视为点电荷也是相对的。其次，一个带电导体即使在某一问题中不能被视为点电荷，但是整个导体可以被分割成若干个带电导体，每一部分都可以被视为点电荷。所以，点电荷的场强叠加原理对于带电导体和带电导体组仍然适用，为此可以引入以下两个结论。

结论一：一个带电导体在空间某点产生的场强等于把这个带电导体无限分割成若干个点电荷后每个“点电荷”单独存在时在该点产生场强的矢量和。

结论二：一组带电导体在空间某点产生的场强，等于这组带电导体相互达到静电平衡后每个带电导体“单独存在”时产生的场强的矢量和。

1）在利用场强叠加原理（即上述两个结论）计算空间某点场强时，带电导体一般是指均匀带电的导体，对于非均匀带电导体在空间产生的场强很难用此方法计算。

2）要注意区分原理中点电荷“单独存在”和结论中导体“单独存在”的不同含义。在原理中所说的点电荷“单独存在”时在空间产生的场强和每个点电荷孤立存在时在空间产生的场强是一样的。因为对于点电荷来说不存在电荷的重新分布问题，而对于带电导体存在电荷重新分布问题。因此，结论中所说的导体“单独存在”是指各带电导体处于静电平衡后的“单独存在”（即各带电导体上的电荷分布应是各导体静电平衡后的电荷分布，参与矢量叠加的电场应是各导体静电平衡后产生的电场，要与各导体“孤立存在”时产生的电场区分开来）。对于这个问题人们往往理解不够深刻，甚至是错误的。下面通过例子说明它们的应用。

【例】求均匀带电细棒中垂直面上的场强分布，高棒长为2L，带电总量为＋Q（见图1）。

【解】该题目是一个均匀带电孤立导体，因此可以用结论一的方法，把这个带电导体无限分割成若干个点电荷，每个“点电荷”单独存在时在该点产生场强的矢量和即所求。

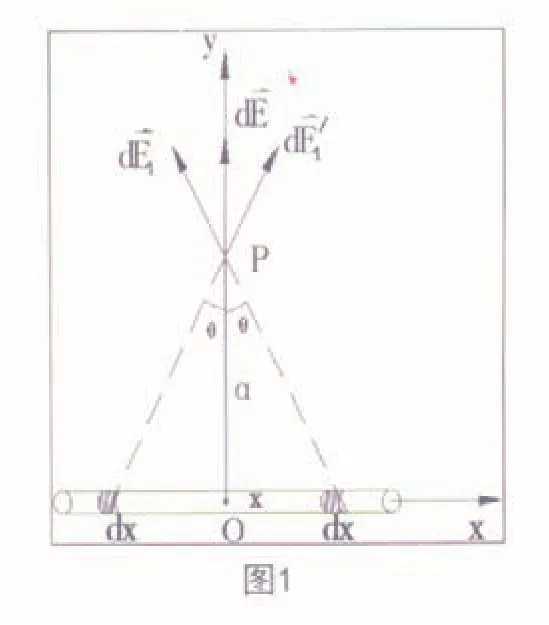
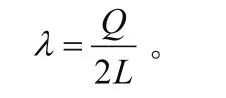
把细棒无限分割成许多小线元，每一线元可视为点电荷，在棒上取x到x＋dx为一线元，长度为dx, 所带电量为dq＝λdx。

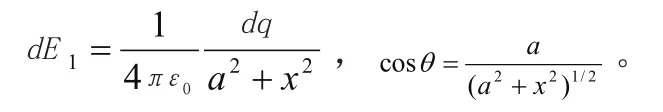
[1]王中健.关于高斯定理和电场和电场叠加问题的再讨论[J].大学物理,1995(4)

[2]阎金铎,李椿,王殖东.普通物理学简明教程[M].北京:中央广播电视大学出版社,1984

[3]梁灿彬.电磁学[M].2版.北京:高等教育出版社,2004