大跨空间结构行波平稳随机地震响应
黄明开
0 引言
目前大跨结构的抗震分析方法一般有反应谱法、随机振动法和时间历程法。常规的反应谱法不能考虑行波效应等复杂的因素。文献[1]介绍了一种由Berrech和Kausel提出的非一致激励反应谱法,文献[2]~[4]对该方法进行了改进。本文在文献[2]~[4]等的基础上进一步将虚拟激励法推广应用于大跨空间网格结构在行波平稳和非平稳地震作用下的随机响应分析,对浦东国际机场候机楼空间结构进行了随机地震响应分析,对比了各种情况下的响应性能,给出了相应结论。
1 结构平稳随机地震响应
对于空间结构体系,假定质量集中在各节点上,且只考虑三维平动地震分量的作用,忽略地震动转动分量的影响,选择相对于地心静止的绝对坐标系,并假定阻尼力与相对速度成正比[5,6],则空间结构体系在多点地震激励下的运动方程可写为[7]:
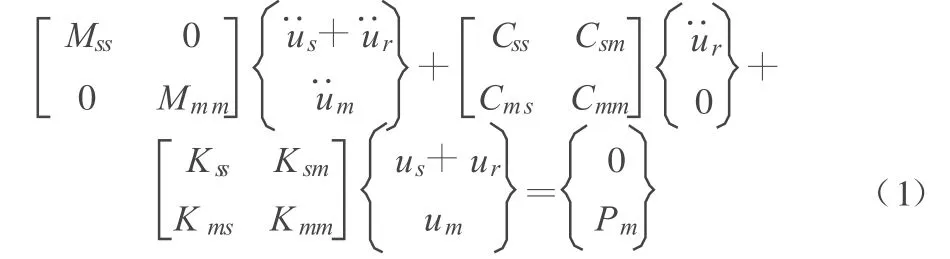
其中,[Mss],[Css],[Kss]分别为结构内部非约束节点(简称自由节点)的质量、阻尼、刚度矩阵;[Mmm],[Cmm],[Kmm]分别为对应于支座约束节点的质量、阻尼、刚度矩阵;[Csm],[Cms]分别为结构内部自由节点和支座节点的耦合阻尼矩阵;[Ksm],[Kms]分别为自由节点和支座节点的耦合刚度矩阵;{us},{ur}分别为自由节点的拟静力位移和相对于支座节点的动力位移;{um}为支座节点的位移向量,即为地面节点强迫位移向量;{Pm}为作用于支座节点上的约束力向量。

将式(2)代入式(1)进一步化简得:

当t=0时,地震输入为一致输入。假设当t=Tj时地震波到达空间结构第j个支座节点(xj,yj),则:
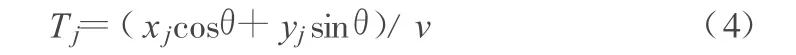
其中,v为地震波等效视波速;θ为地震波传播方向与结构x轴方向之间的夹角。
当考虑地震为平稳随机过程时,根据虚拟激励法原理,可得结构在第j个激励作用下结构的稳态响应为:
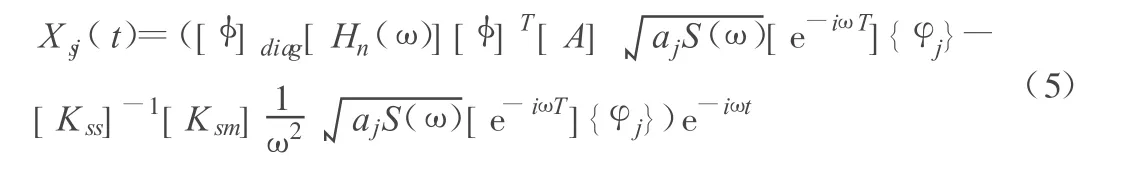
其中,[φ]为结构振型矩阵;{φj}为第j阶振型;Hn(ω)为频响函数S(ω)为输入的功率谱矩阵;aj为S(ω)的矩阵特征值;T为相对于原点的运动时间差。式(5)等号右边前半部分为结构的动力响应,后半部分为结构的拟静力位移响应。
当考虑行波输入后,沿地震波传播方向的一条直线上j,k两点的互功率谱Sjk(iω)可用下式计算[8]:

其中,va为视波速;ρjk(ω,djk)为描述两点地震动的相关程度量,它考虑了结构不同激励点间的部分相干效应。国内学者借鉴我国抗震规范确定设计反应谱曲方法、取各模型在各次地震中确定的相干值的平均值,然后根据平均值给出一个模型。该模型适用于21πrad/s以下的频率成分,对于频率比较低的大跨空间结构,具有普遍的代表性,其表达式如下:
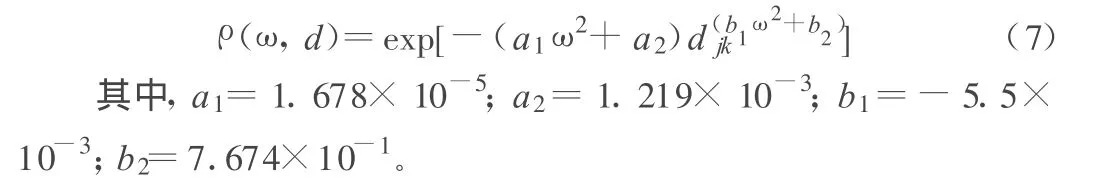
2 工程算例
2.1 工程概况
浦东国际机场二期航站楼由航站主楼、候机长廊、二者间的连接部分以及与三者均相邻的捷运车站组成,文献[9]给出了该工程相关构件的截面、材料及特征杆件节点和振动特性等。
2.2 地震波、工况和计算结果
地震波选用El-Centro波,为了更好地显示地震平稳随机激励下视波速对结构响应的影响,本文选取了典型节点、柱和梁,分别考虑了一致输入,1 000 m/s,500 m/s,200 m/s和100 m/s五种工况下节点、柱和梁的位移、轴力及弯矩的方差,并绘成图1~图5。
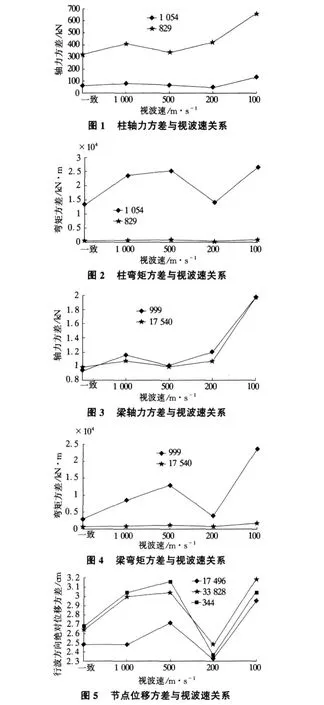
从图1~图5可知,大跨度空间结构地震动的行波效应有显著的影响,行波效应的影响与地震波的传播速度有很大的关系。一般来说,当地震波传播速度很大时,各点的输入相对一致,结构反应趋于甚至低于一致地面运动作用下的反应;随视波速的减小,结构地震反应随之增大,呈近似线性关系;而当视波速较低时,各点的输入大不一致,行波效应会产生很大的影响,且当视波速非常小时,出现地震激励在结构首尾支座之间作用的时间差太大,适用波动理论,而仍用动力学方法分析的结果存在着误差;算例中位移的影响也有变小的情况,但其影响往往比较大,当视波速很小时,可以增大到1.8倍左右。柱脚的弯矩和与柱连接处杆件的轴力明显增大,可以增大到2倍左右。地震观测证实,一般情况下地震动水平视波速大于1 000 m/s[10],所以根据场地情况选取最小视波速进行大跨度空间结构地震动的行波效应分析是比较合理和可靠的。
3 结语
1)大跨度空间结构地震动的行波效应对与行波方向一致的结构响应有显著的影响,对其他方向的影响比较小。算例中位移的地震响应最大位置发生在结构的角点和边线上。
2)行波效应的影响与地震波的传播速度有很大的关系。在某一范围内的地震波传播速度会产生最大的结构反应。
3)地震观测证实,一般情况下地震动水平视波速大于1000 m/s,因此,在考虑大跨度空间结构地震行波效应时,至少应根据场地情况选取最小视波速进行地震动的行波效应分析。
[1]Mounir K.Berrech,Eduardo Kausel.A model cordial combination rule for spatially varying seismic motions[J].Earthquake Engineering and Structural Dynamics,1993,22(9):791-800.
[2]林家浩.随机地震响应功率谱快速算法[J].地震工程与工程振动,1990,10(4):38-46.
[3]林家浩,钟万勰.关于虚拟激励法与结构随机响应的注记[J].计算力学学报,1998,15(2):217-223.
[4]刘先明.大跨度空间网格结构多点输入反应谱理论的研究与应用[D].南京:东南大学博士学位论文,2003.
[5]林家浩,钟万勰,张亚辉.大跨度结构抗震计算的随机振动方法[J].建筑结构学报,2000,21(1):29-36.
[6]李建俊.随机地震响应分析的虚拟激励法[D].大连:大连理工大学工程力学研究所,1994.
[7]薛素铎,王雪生,曹 资.空间网格结构多维多点随机地震响应分析的高效算法[J].世界地震工程,2004,20(3):9-13.
[8]屈铁军,王君杰,王前信.空间变化的地震动功率谱的使用模型[J].地震学报,1996,18(1):67-85.
[9]楼梦麟,黄明开.上海浦东机场(二期)候机楼水平地震行波效应时程分析[J].建筑结构,2009,39(2):8-11.
[10]范立础,王君杰,陈 玮.非一致地震激励下大跨度斜拉桥的响应特征[J].计算力学学报,2001,18(3):358-363.

