不同环境影响下共形蝶形天线性能的理论分析

胡慧琳 谭云华 朱柏承 周乐柱

(北京大学信息科学技术学院,北京100871)

1.引 言

作为现代天线领域的重要组成部分,共形天线已吸引学术界越来越多的关注。尤其是在高速运动的载体上,与载体共形的天线不会由于对物体的空气动力外形造成破坏而产生额外的气动阻力,却又能实现天线的固有特性,因而在导弹、卫星、舰船和个人通信等领域的应用将日益普遍[1]。

在不同应用背景下,环境因素对共形天线性能造成的影响不容忽视。一方面,现代战争对载体的隐身性能要求越来越高。当天线共形在载体表面时,不可避免地面临被探测到的威胁,因此,对天线的雷达散射截面(RCS)研究也非常必要。除了改善载体的物理结构以外,一个非常有效的方法就是在载体表面涂覆吸波材料以降低RCS。在天线表面涂覆不同吸波材料将对共形天线的RCS性能产生重要影响。而在雷达探测时,共形天线往往都是处于工作状态,故其馈源必定会对 RCS造成相应影响。另一方面,实际工作中的天线也常常会受到外界入射场的影响。因此,入射场对其辐射方向图的改变也将严重影响共形天线的性能。

常见的共形天线分析算法主要有:积分方程法[2]和微分方程法[3-4]。积分方程法计算精确,但缺点是计算过程中形成的矩阵为满秩,计算量较大;典型算法如边界积分方程法(BI)[5-6],体积分方程法(VIE)[7-8],以及时域积分方程法(TDIE)[9]等。微分方程法计算较简便,尤其对复杂结构和电大尺寸空间问题处理较好,但缺点是边界处理起来比较困难;典型算法如有限元方法(FEM)[10],时域有限差分法(FDTD)等。经过综合比较,文中采用基于有限元法和边界积分方程法的混合算法(FE-BI),该方法结合了二者的各自优点,不仅可以对边界准确建模,还可以解决具有复杂几何结构和介质分布的问题,因此非常适用于共形天线分析。

尽管FE-BI是较为成熟的算法,也有不少文献应用于电磁辐射和散射问题[11-12],但是应用该方法对共形天线的辐射和散射特性进行系统分析的文献则很少见。论文在详细介绍FE-BI算法用于辐射和散射问题的原理及公式的基础上,以典型的平面和圆柱共形蝶形天线为例,系统分析了不同环境下共形蝶形天线的性能:首先详细分析了共形天线的一般辐射性能以及散射特性;然后讨论了表面涂敷不同介质涂层对天线性能的影响;最后结合天线的实际工作情况,分析了在工作状态下考虑馈源影响的共形天线的散射特性,以及有入射场影响时的天线方向图的变化。结果表明:不同环境情况下天线的辐射和散射性能均有较大改变,环境因素成为天线设计中不容忽视的问题。

2.FE-BI方法原理

如图1所示,用有限元-边界积分方程法分析处于复杂环境中的天线问题的方法如下:首先,用一个真实的封闭结构包围整个天线体(内部可以填充各向同性介质或者各向异性复杂介质);然后以封闭体表面为界,对边界内和边界上的场分别用有限元法和边界积分方程法进行建模和计算;最后应用场的连续性原理把二者结合起来,求解联合方程获得辐射问题或散射问题的场。

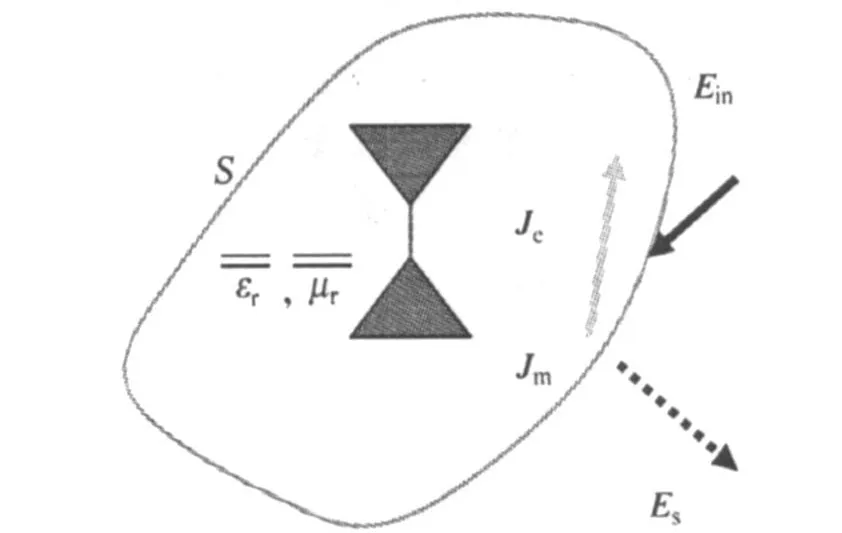
图1 处于复杂环境中的天线问题

2.1 辐射问题

处理一般辐射问题时,认为没有入射场和散射场项,即图中的E in=0,E S=0。由微分形式下的麦克斯韦方程组出发

▽×E=-Mi-jωμ0μr H (1)

▽×H=Ji+jωε0εr E (2)

假设外表面没有外加磁流,通过矢量运算,并用特征函数展开电场,并把方程改写成矩阵形式,同时把未知的电场系数分为内部场和外部场两部分,可以得到矩阵方程

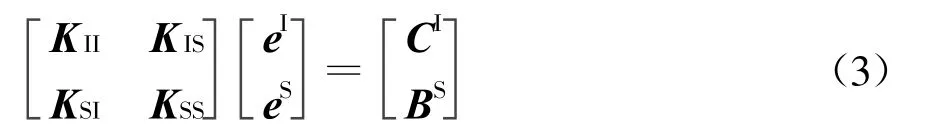
式中:[K]是有限元产生的稀疏的、对称的阻抗矩阵;而[CI]代表体积V内的电流源和磁流源的贡献;

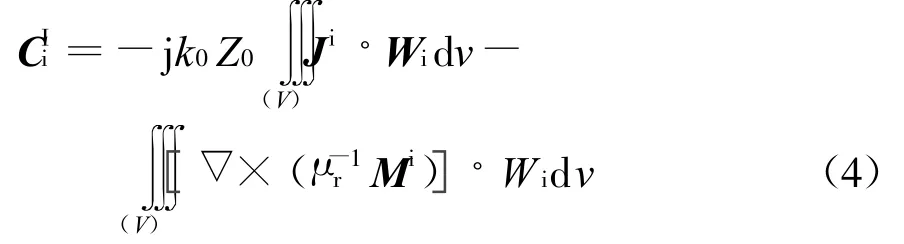
[BS]代表表面电流的贡献。在FE-BI方法中,这一项表示等效面电流,因此,我们可以把[BS]项写成

式中:[B]是一个N×N矩阵;[bS]为N×1矢量,故方程(3)可以简化为

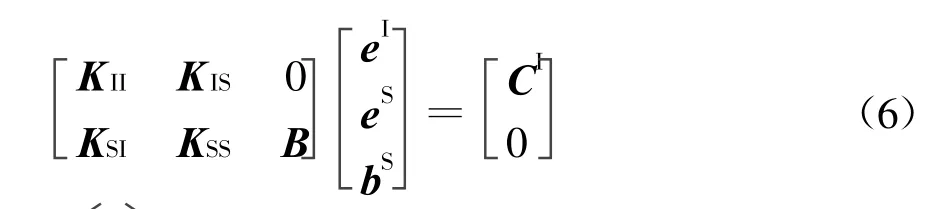
再考虑外部区域场的情况。根据场等效原理,可以用表面电流JS=n×HS和表面磁流MS=ES×n的形式来表示区域外部的场,从中可以得到电场积分方程(EFIE)、磁场积分方程(MFIE)以及混合场积分方程(CFIE)

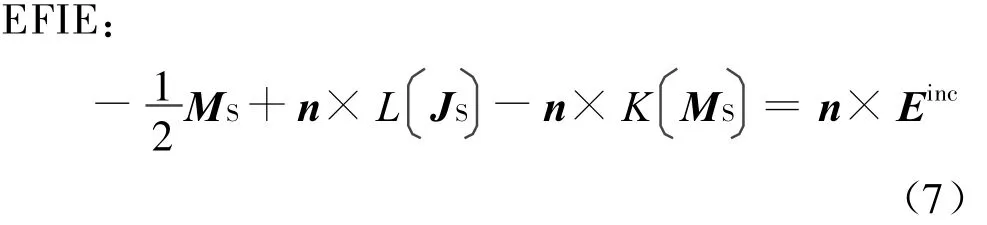
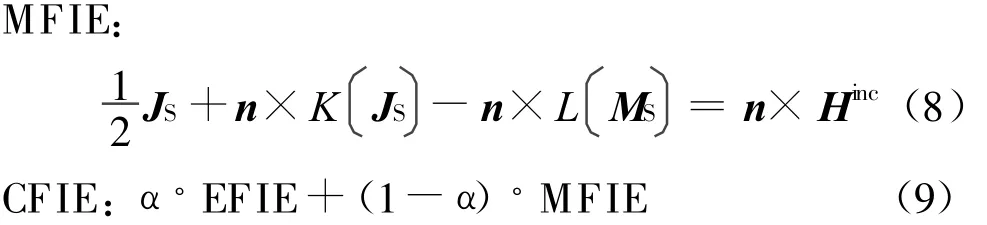
式中 ,α∈(0,1),

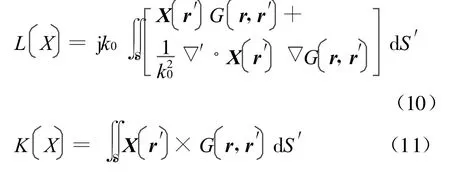
把J S和M S用RWG基函数展开,离散化混合场积分方程,可以得到矩阵方程,

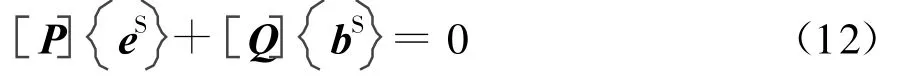
式中,方程左边的[P]和[Q]为N×N的满秩矩阵,而在没有入射场时,方程右边为 N×1的零矩阵。联合方程(6)和方程(12),可以得到方程组

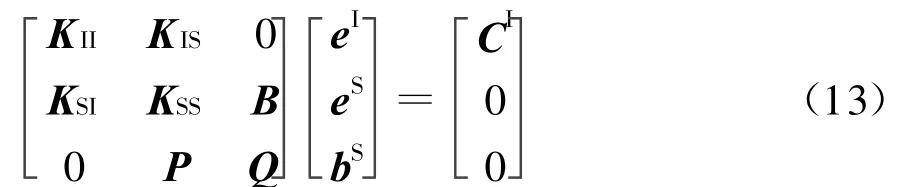
2.2 散射问题

在天线散射问题中,由于在有限元区域内无源,故式(6)中

有限元区域的方程变为

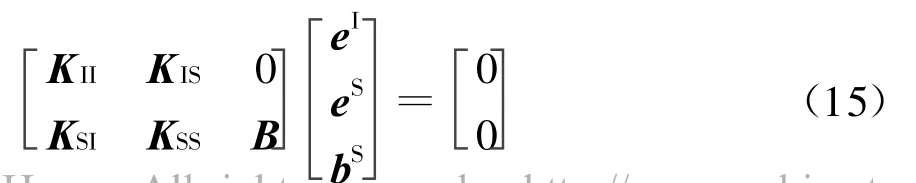
加入入射场,则式(12)右边不为零

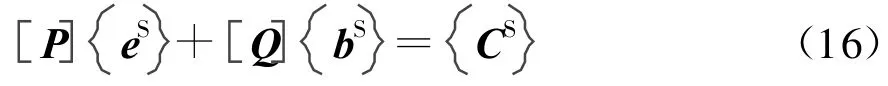
联合方程(15)(16),得到了适用于散射问题的FE-BI方程

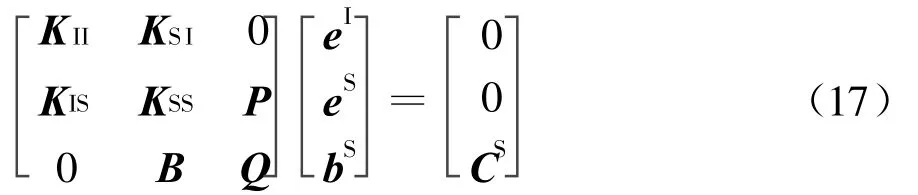
2.3 有馈电的散射问题及有入射场的辐射问题

在处理有探针馈电时的散射问题,以及入射场对方向图影响时,FE-BI方程则有馈源项和入射场两项。得到该情况下的FE-BI方程

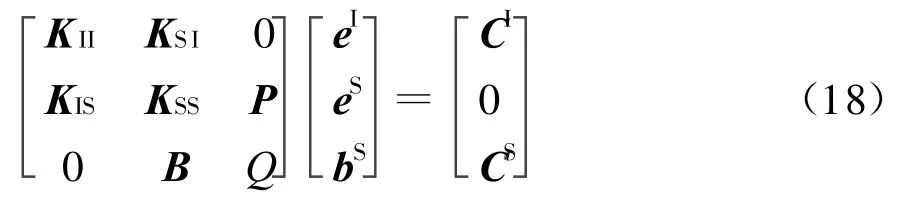
各项的物理意义如前所述。

3.仿真结果分析

基于上面推导的FE-BI公式,我们对典型的平面和圆柱共形蝶形天线的辐射和散射特性进行了分析。其结构如图2所示。

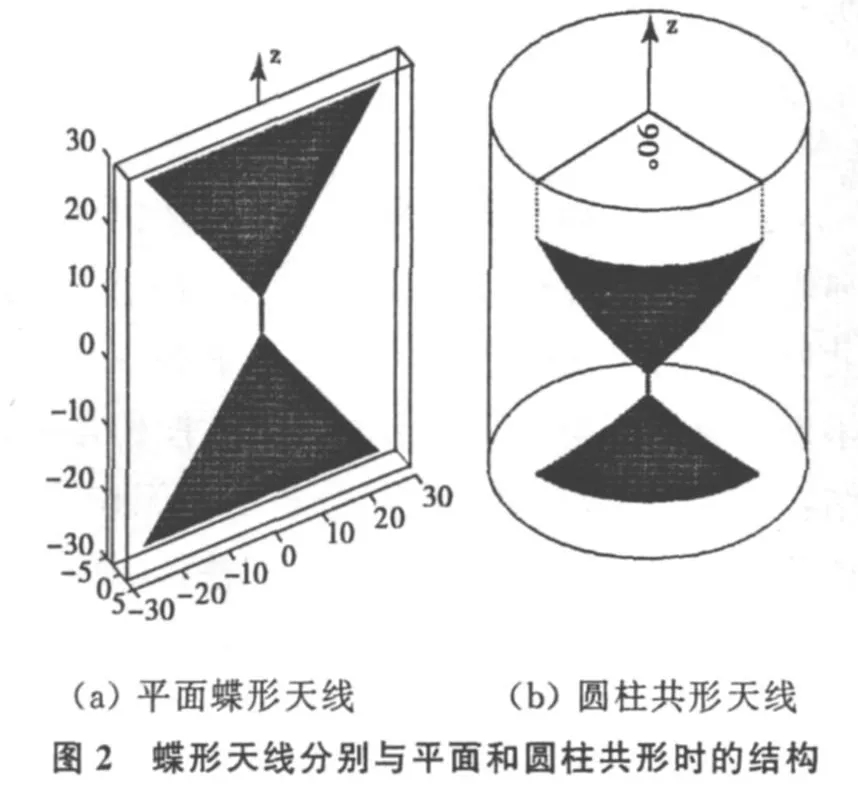
3.1 平面共形蝶形天线的辐射

首先以工作频率为3GHz的平面蝶形天线为例(如图2(a)所示),验证算法及程序的正确性。为便于比较,天线尺寸参数与文献[13]的相同,如表1。由文中FE-BI方法和程序得到其辐射方向图,与文献[13]FDTD方法模拟及测量的结果较好吻合,验证了该方法的正确性,比较结果参见文献[14]。

表1 平面共形蝶形天线尺寸

3.2 圆柱共形蝶形天线的散射

下面分析共形蝶形天线的散射特性。以圆柱共形蝶形天线为例,该天线为共形于圆柱体表面的完全电导体。天线的结构如图2(b),天线参数如表2所示。入射波沿负Z轴方向。

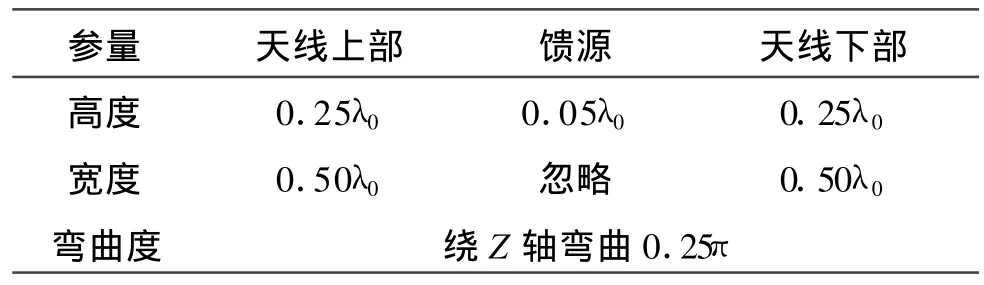
表2 圆柱共形天线尺寸

图3对比了平面与圆柱共形情况下的双站RCS,可以看出蝶形天线与圆柱面共形以后,其RCS大大降低。

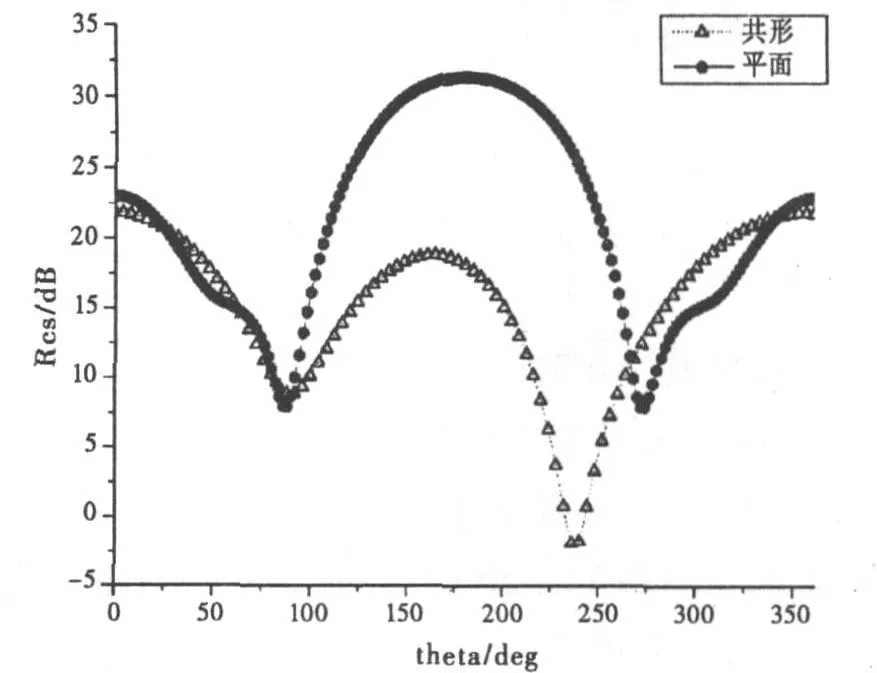
图3 蝶形天线RCS(圆柱共形与平面情况对比)

3.3 涂覆不同介质层的情况

下面以涂覆正单轴各向异性介质、负单轴各向异性介质为例,分析了天线表面涂敷不同介质对天线散射特性的影响。该涂敷层厚度均为0.025λ0,介质参数分别为[15]:

正单轴各向异性介质:

负单轴各向异性介质:

图4给出了仿真结果。与图3相比,涂敷吸波材料后,与未涂敷介质的共形蝶形天线相比后向RCS大大减小。而在涂敷层厚度相同的情况下,负单轴各向异性介质对缩减RCS的效果要优于正单轴各向异性介质。

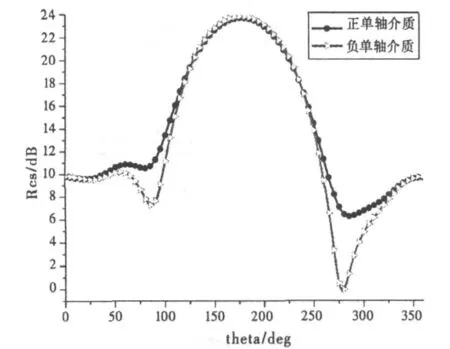
图4 分别涂敷正单轴介质和负单轴介质时的共形蝶形天线RCS曲线

3.4 有馈电时共形天线的RCS

实际天线处于工作状态,必须考虑馈电对天线性能的影响。下面以平面共形蝶形天线为例进行分析,其结构如图2(a)所示,相应尺寸参数如表1,馈源沿Z轴方向放置。图5对比了有馈源和无馈源情况下的E面RCS。

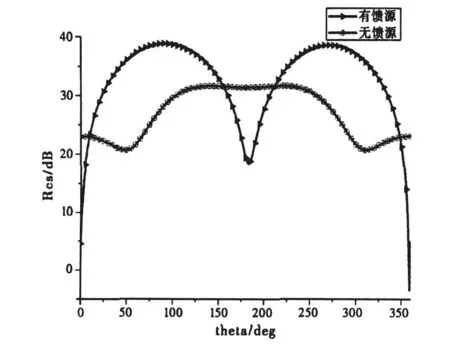
图5 有馈源和无馈源情况下E面RCS

可见,增加馈源项导致天线的RCS发生较大改变。对于平面共形蝶形天线而言,当增加Z轴方向的激励场时,后向RCS明显减小,而其它方向RCS增大。

3.5 有入射场时共形天线的辐射问题

图6以平面共形蝶形天线的E面方向图为例,分析了有入射场时天线的辐射特性的变化。入射场沿负Z轴方向。图中圆点线为无入射场时的方向图,三角点线为加入入射场后的方向图。

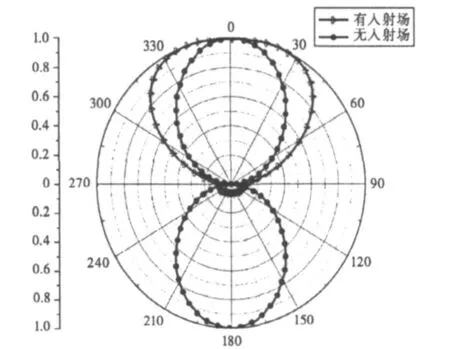
图6 平面蝶形天线有入射场时的方向图

由此可见,在散射场强度与馈源强度相似情况下,天线方向图改变较大。当入射场沿负Z轴方向时,沿逆入射场附近方向的辐射加强,而沿入射场附近方向的辐射减弱。这对被照射的天线而言,意味着改善了天线的前向辐射性能。

4.结 论

文章采用有限元-边界积分方程方法分析了不同环境情况下的共形蝶形天线性能。首先详细分析了共形天线的一般辐射性能以及散射特性;然后讨论了表面涂敷不同介质涂层对天线性能的影响;最后结合天线的实际工作情况,分析了在工作状态下考虑馈源影响的共形天线的散射特性,以及有入射场影响时的天线方向图的变化。仿真结果表明:天线表面涂覆负单轴各向异性介质对缩减RCS的效果更好。而在工作状态下,由于馈源的作用,使得天线的后向RCS明显减小。此外,在一定条件下,入射波对天线辐射特性的影响也比较明显,会改变天线的方向性。当然,这些结论是在模拟平面和圆柱共形蝶形天线的特殊情形下做出的,对于其他类型的天线在不同的共形表面的更为实际的情况,这些结论是否成立,还必须进行具体的模拟和分析,这是值得深入研究和有实际应用价值的研究课题,也是作者下一阶段的工作内容之一。

[1] JOSEFSSON L,PERSSON P.Conformal Array Antenna Theory and Design[M].Hoboken,NewJersey:IEEE Press,2006.

[2] 王 湃,夏明耀,周乐柱.导体-介质组合体散射分析两种积分方程法比较[J].电波科学学报,2007,22(4):546-551,556.

WANG Pai,XIA Mingyao,ZHOU Lezhu.Comparison of two integral equation approaches for analysis of scattering by combined conducting and dielectric bodies[J].Chinese Journal of Radio Science,2007,22(4):546-551,556.(in Chinese)

[3] ALU A,BIOLOTTI F,VEGNI L.Method of lines numerical analysis of conformal antennas[J].IEEE Trans Antennas Propagat,2004,52(6):1530-1540.

[4] MACON C A,KEM PEL L C,SCHNEIDER S W,et al.Modeling conformal antennas on metallic prolate spheroid surfaces using a hybrid finite element method[J].IEEE Trans Antennas Propagat,2004,52(3):750-758.

[5] SHIN K,FUKAI I.Application of boundary-element method to electromagnetic field problems[J].IEEE Trans Microwave Theory and Techniques,1984,32(4):455-461.

[6] BREBBIA C A.The Boundary Element Method for Engineers[M].London:Pentech Press,1978.

[7] SCHAUBERT D H,WILTON D R.,GLISSON A W.A tetrahedral modeling method for electromagnetic scattering by arbitrarily shaped inhomogeneous dielectric bodies[J].IEEE Trans Antennas Propagat,1984,32(1):77-85.

[8] GRAGLIA R D.The use of parametric elements in the moment method solution of static and dynamic volume integral equations[J].IEEE Trans Antennas Propagat,1988,36(5):636-646.

[9] 赵延文,聂在平,徐建华,等.时域电场积分方程的稳定求解[J].电波科学学报,2004,19(2):148-152.

ZHAO Yanwen,NIE Zaiping,XU Jianhua,et al.A stable solution of time-domain electric-field integral equation[J].Chinese Journal of Radio Science,2004,19(2):148-152.(in Chinese)

[10] TAN Yunhua,ZHOU Lezhu,ZHANG Yaojiang.A-nalysis of electromagnetic scattering f rom 3-D conductors coated with anisotropic inhomogeous materials using the FEM-FMA[J].2002 3nd IEEE International Conference on Microwave and Millimeter Wave Technology Proceedings,ICMMT 2002:622-625.

[11] PENG Zhen,SHENG Xinqing.A flexible and efficient higher order FE-BI-MLFM A for scattering by a largebody with deep cavities[J].IEEE Trans Antennas Propagat,2008,56(7):2031-2042.

[12] 周 平,徐金平.FEM/BEM混合法计算各向异性不均匀介质柱电磁散射[J].电波科学学报,2006,21(4):619-623.

ZHOU Ping,XU Jinping.Computation of EM scattering by a two-dimensional anisotropic inhomogeneous cylinder with thehybrid finite element-boundary element method[J].Chinese Journal of Radio Science,2006,21(4):619-623.(in Chinese)

[13] SHLAGER K L,SMITH G S,MALONEY JG.Optimization of bow-tie antennas for pulse radiation[J].IEEE Trans Antennas Propagat,1994,42(7):975-982.

[14] HU Huilin,TAN Yunhua,ZHU Bocheng,et al.A-nalysis of Conformal Bow-tie Antenna Scattering by Using the Hybrid FE-BI Method[C]//8th International Symposium on Antennas,Propagation and EM Theory,November 2-5,2008:898-901.

[15] YANG Helin,LIU Wu,LU Shu.EM Scattering by Rectangular Conducting Flat Plates with the Uniaxial Anisotropic Materials[C]//CEEM2000 Proceedings Environmental Electromagnetics,2000:213-216.