基于遗传算法的大地电导率反演

蒲玉蓉 席晓莉 朱 虹 周丽丽

(西安理工大学自动化与信息工程学院,陕西 西安710048)

1.引 言

近些年,随着GPS自身缺陷的日益暴露,以及许多国家对战时使用GPS的可靠性的诸多担心,将改进的罗兰C(如E罗兰)系统作为GPS的备用系统,在授时及导航领域的应用重新受到各国的广泛重视[1-3]。其中低频无线电地波传播时延修正的理论预测及试验测量是提高罗兰C精度的关键技术,而大地电导率的确定是精确预测地波传播时延的前提。大地电导率可以通过许多方法确定,最有效也是最常用的方法是通过测量低频地波的场强或时延来进行反演[4-5]。

因此,如何通过测量低频地波传播的场强或时延反演出传播路径上的大地电导率成为地波传播时延修正量理论预测的核心问题。

在已知电导率分布条件下预测复杂路径上低频地波传播时延的理论方法基本成熟,如WAIT J R方法、Millington经验公式法、波模转换法、积分方程方法和抛物方程方法等[6-10]。因此,文章将地波传播时延理论预测方法作为前向算法,以多点时延修正量的理论预测结果与实测结果均方误差最小为优化目标,把大地电导率反演问题转化为优化问题。其中前向算法采用工程应用最为广泛的Millington经验公式方法;优化算法采用在许多领域都取得成功应用的智能优化算法——遗传算法。利用该算法,在已知传播时延修正量测量结果的传播路径上对大地电导率进行反演,然后把大地电导率的反演结果推广应用到附近区域,并应用该电导率分布对其传播时延修正量进行理论预测,通过比较理论预测时延与实测时延之间的误差,验证算法的可行性及可靠性。

2.算法原理

2.1 Millington经验公式

当收发天线都位于地球表面时,低频地波传播时延可以表示为[9]

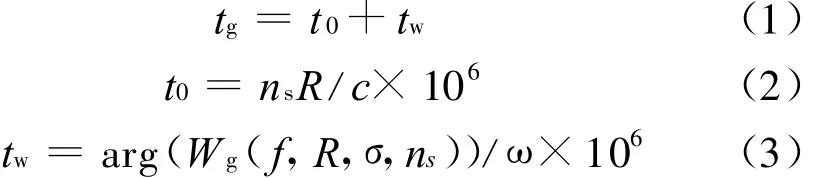
式中:tg为地波传播时延,单位为μs;t0为基本时延(也称为一次相位因子);t w为二次时延(也称为二次相位因子);R是收发两点间大圆距离,单位为km;ns是传播路径上平均大气折射指数;c是光速;σ是传播路径上的电导率,单位为S/m;arg(W g(f,R,σ,ns))是地波衰减因子的幅角。

假设传播路径根据电导率的不同可以分为n段 ,各段电导率依次为 σ1,σ2,…,σn,其对应的大圆距离分别为R1,R2,…,Rn(如图1)

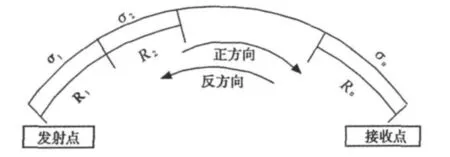
图1 n段复杂路径图

则n段复杂路径地波衰减因子可表示为[9]

式中:

式中:每一段路径上地波衰减因子W(Ri,σi)的计算可参见文献[9],由公式(1)～(3)就可以计算出地波传播时延。

2.2 遗传算法

遗传算法(Genetic Algorithm,GA)是由美国Michigan大学的J.Holland教授于1975年受达尔文生物进化论的启发而提出的。它模拟了自然选择和生命遗传中发生的选择、交叉和变异等现象[11]。目前遗传算法在很多领域都取得了成功的应用,并在电磁学领域得到了广泛应用[12]。

遗传算法主要涉及五大要素:编码、群体初始化、适应性函数的设定、遗传操作的设计和控制参数的设定。即首先采用某种编码方式将解空间映射到编码空间,每一个编码对应问题的一个解;其次随机确定起始的一群个体作为初始种群;而后针对所要解决的问题定义适应度函数;最后根据适者生存原理按照适应度大小选择个体,并借助遗传算子对个体进行交叉和变异操作,生成代表新的解集的种群,如此循环迭代,直到寻找到问题的最优解[11]。

2.3 基于遗传算法的大地电导率反演

鉴于遗传算法具有全局寻优能力、可操作性强等优点,尝试将其应用到大地电导率的反演中。其具体操作过程如图2所示:

1)对各测量点所对应传播路径提取其高程信息,并根据传播路径上的地形起伏变化规律对其进行分段处理,每段取同一电导率值。

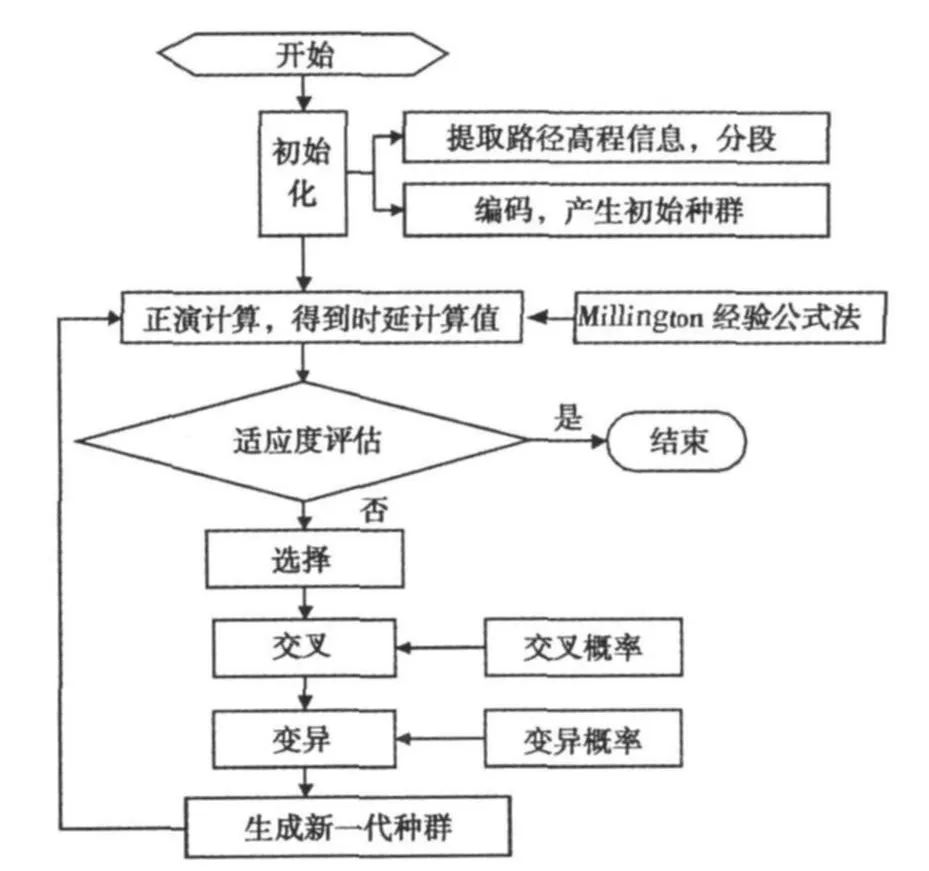
图2 基于遗传算法的大地电导率反演流程图

2)编码和初始化:假设有L个测量点,且其传播路径都经历了 m 个电导率(即 σ1,σ2,…,σm)区域,则首先依据经验给定每个区域的电导率取值范围 [,];其次采用实数编码产生初始种群Ab;同时设定遗传算法中的种群规模、交叉概率、变异概率和最大迭代次数。

3)正演计算:依据Millington经验公式对种群Ab中的每组个体都可以得到一个传播时延的理论预测值tw预测。

4)适应度评估及遗传操作:利用适应度函数判断是否达到要求,如果没有达到,则利用遗传算子中的选择、交叉和变异操作得到下一代种群,并继续上面的步骤,直到得到最优解。

其中适应度定义为:L个测量点传播时延理论预测值与实测值之间的均方误差。

当误差达到我们所预设的适应度阈值ε时,其所对应的一组个体为最优解,即为各区域的电导率值。

3.算法应用

3.1 实验区分布

传播时延的实测区位于宣城台到上虞附近区域,实测数据为宣城台发射的罗兰信号的传播时延,实测点位于以宣城台为中心,以北向为参考,方位角为122°～123°的扇形区域,在此区域内共有 7个测量点,其分布如图3所示。

3.2 传播时延的测量方法

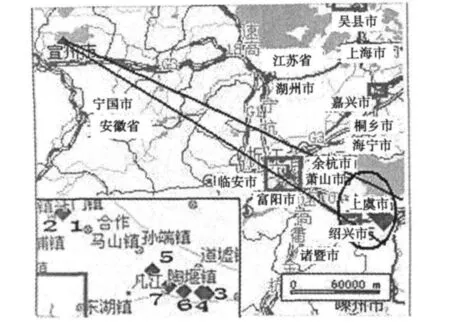
图3 仿真所选实验区域

传播时延采用THC-IGPS综合测试校频仪、罗兰数字接收机和HP53131A数字计数器测量,系统构架如图4,其中GPS接收机获得接收点经纬度坐标和GPS秒信号,罗兰数字接收机获取以本机时钟为参考的罗兰信号到达时刻及导航电文,数字计数器给出本机秒信号与GPS秒信号间的时差,上述仪器的测量结果经USB口上传到计算机。

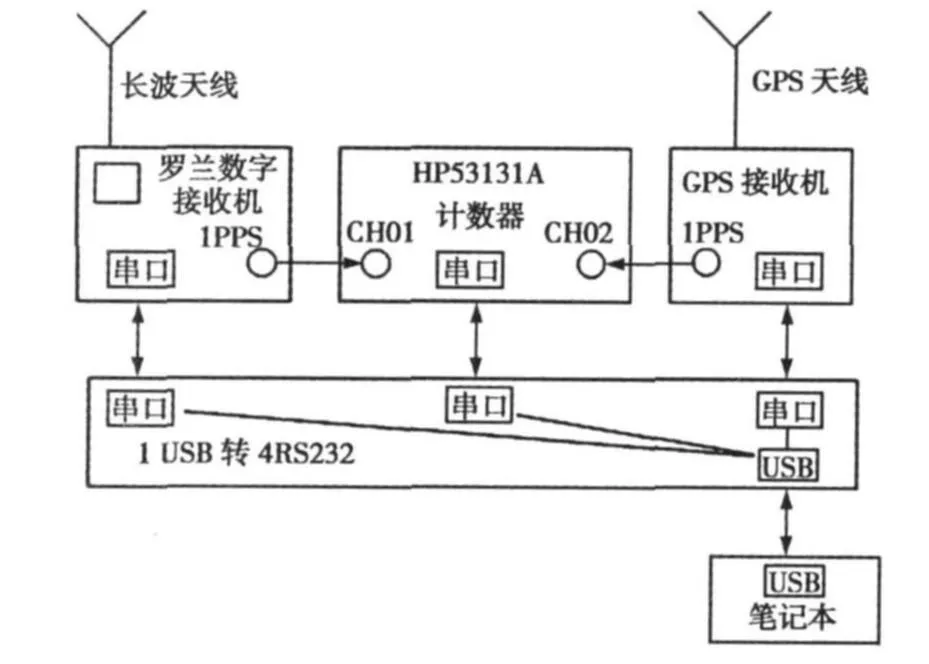
图4 传播时延测量仪器构架图

对上述测量结果进行处理可得到以GPS时为参考的罗兰信号到达时刻,从罗兰电文中提取信号发射时刻,可得到信号的传播时延tg;采用GPS接收机给出的测量点经纬度,宣城发射台经纬度已知,可计算出收发点间的大圆距离R;这样,利用公式(1)和(2)就可以得到二次时延tw。

对实验中所选取的7个观测点均进行5分钟的测量,每点可获取300个传播时延tg测量值,对其求取均值及方差后作为此点的测量结果。图5即为这七个观测点的测量结果,其中符号*表示各观测点的tg测量值均值,上下浮动表示其方差。

3.3 传播路径的分段处理

图5 各观测点测量结果图

传播路径的电导率主要与传播路径上的地质结构、植被覆盖、地面或地上建筑物、气候等因素有关,文章的实验区面积较小,均处于南方海相沉积地质区域,影响电导率数据的主要因素是地形结构。因此可依据传播路径的地形变化对电导率进行分段。

从数字化地理信息系统分别提取宣城台到7个测量点路径的高程信息,如图6所示(注:为了方便划分电导率分布区域,将这几条路径的高程分布图叠加在了一起)。由图可以看出实验区所有测量点的传播路径起伏信息基本一致,均为“丘陵-平原”结构,可将其分为两个区域:0～132 km内为区域一,取电导率 σ1;132～220 km 内为区域二,取电导率 σ2。

图6 各测量对应传播路径高程信息

3.4 基于遗传算法的电导率反演

采用遗传算法,选用7个测量点中的3个(1点、4点和7点)对传播路径的电导率σ1和σ2进行反演,用其余4个测量点对反演结果进行验证。

遗传算法的参数设置:电导率取值范围:第一段为丘陵,电导率较小,取值范围可选为(0.0001,0.001),第二段为平原,电导率较大,取值范围可选为(0.001,0.01),单位为 S/m;种群规模:50;交叉概率:0.8;变异概率:0.1;最大迭代次数:100;适应度阈值:0.01μs。

图7是采用遗传算法独立运行20次的电导率反演结果。

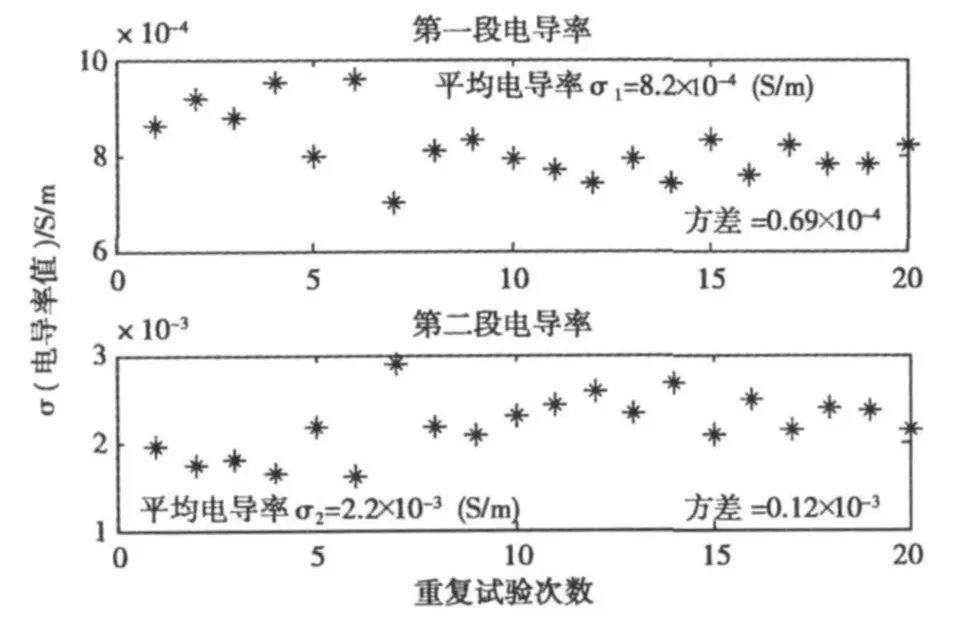
图7 重复实验20次各区域等效电导率分布

将重复实验20次所反演的区域一和区域二的电导率均值分别应用到测量点2、3、5、6所在的路径,应用Millington经验公式预测其时延tw,比较时延理论预测值与时延测量值之间的误差,结果示于图8。

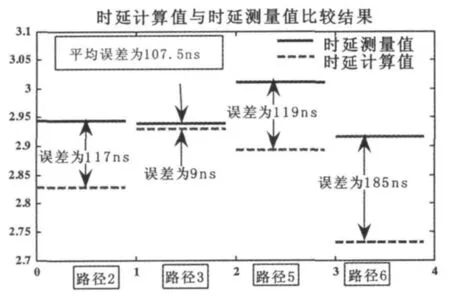
图8 时延计算值与时延测量值比较结果图

从图8可以看出,将遗传算法反演出的电导率分别应用到其余未参与反演的路径时,其时延理论预测值与时延测量值之间的误差较小,平均误差为107.5 ns,最大误差为185 ns,在我们可接受的误差范围内。可以认为所反演出的电导率能够作为区域一和区域二的电导率。

4.结 论

文章以Millington经验公式为前向算法,将大地电导率反演问题看成一个多参数优化问题,应用遗传算法对其进行反演。文中选取了宣城台到上虞附近的一个小扇形区域进行传播时延的实验测量;采用高程信息进行扇形区域电导率的分区;用遗传算法反演出的各区域的电导率;将所反演出的电导率应用到未参与反演路径中进行误差验证。反演结果说明这种方法所反演的大地电导率是可靠的。

需要说明的是,这里所反演的电导率是“大地等效电导率”,即将各种复杂因素,如地形、地质、土壤种类、地面植被、水文及变化着的气象等对地波传播的影响都归结为电导率的影响。因此它不能应用于其它前向算法,如积分方程方法、抛物方程方法中进行地波传播的场强和时延的精确预测。

[1] National Security Space Office(NSSO).National Positioning,Navigation,and Timing Architecture Study,Final Report[R].Washington DC,2008.

[2] 吴 海,边玉敬,李志刚.罗兰-C最新进展及其对我国相关系统改造的启示[J].陕西天文台台刊,2000,23(1).

WU Haitao,BIAN Yujing,LIZhigang.Recent Development of Loran-C and Some Suggestions[J].CSAO Publications.2000.23(1).(in Chinese).

[3] JOHNSON G W,SWASZEK P F.An Evaluation of eLoran as a Backup to GPS[C]//2007 IEEE Conference on Technolo-gies for Homeland Security,2007:95-100.

[4] IEEE Sts 356-1974.IEEE guide for radio methods of measuring earth conductivity[S].1974.

[5] RA L R,JOSÉM R,JORGE M.Alterna-tive methods to obtain ground conductivity[J].IEEE Transactions on Broadcasting,2009,55(2):282-289.

[6] WAIT J R.The ancient and modern history of EM ground-wave propagation[J].IEEE Antennas and Propagation Magazine,1998,40(5):7-24.

[7] GESNY H,RAVARD O.Propagation over irregular terrain in the VHF band a review of integral equation models[C]//in National Conference on Antennas and Propagation,M ar.30-Apr.1,1999,pp.61–64.

[8] 潘威炎,彭怀云,张红旗.非均匀光滑球面地波衰减因子的抛物方程算法[J].电波科学学报,2006,21(1):37-42.

PAN Weiyan,PENG Huaiyun,ZHANG Hongqi.Parabolic equation algorithm of wave attenuation along inhomogeneous smooth ground[J].Chinese Journal of Radio Science,2006,21(1):37-42.(in Chinese).

[9] 潘威炎.长波超长波及长波传播[M].成都:电子科技大学出版社,2004.

[10] 熊 皓,等.无线电波传播[M].北京:电子工业出版社,2000:359.

[11] 王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002.

[12] HAUPT R L,WERNER D H.Genetic Algorithms in Electromagnetics[M].IEEE Press/Wiley Interscience Publication,2007.