基于BP神经网络的介质圆柱体逆散射方法研究

张清河

(三峡大学理学院,湖北 宜昌 443002)

1.引 言

逆散射研究广泛应用于地震学、目标识别、探地雷达(GPR)、医学成像、地球物理观测和一些无损检测。然而,由于问题本身固有的非线性特征和不适定性,使得逆散射研究显得十分困难,特别是当目标的电尺寸可与入射波长相比拟或目标是介质体时。过去十年,逆散射研究得到了极大的关注,特别是在微波成像和目标重构等领域。有两类问题经常引起人们的兴趣,第一类是确定目标的位置和外部边界,第二类是定性或定量地重构目标的电磁参数(如相对介电常数、电导率等)。许多算法及技术被应用于该领域,传统的优化迭代方法,如Born迭代、变形Born迭代、New ton-antorovitch算法、模拟退火、遗传算法等[1-5]被提出并成功地应用于电磁逆散射问题,但由于在每次迭代中都要计算一次正散射问题,耗费了大量的计算资源和计算时间,不利于对目标的实时逆散射研究。

近年来,神经网络得到了极大的关注并被成功地应用到逆散射问题,这些应用主要集中在静电场问题[6]、不同类型土壤和植物的识别[7]、雨及雪花参数的分析[8-9]及目标的分类[10]等方面。由于人工神经网络具有强有力的学习能力和非线性映射能力,它不需要任何先验公式就可以通过学习或训练自动总结出数据间的函数关系,许多用传统信息处理方法无法解决的问题采用神经网络取得了良好的效果。本文将人工神经网络这一人工智能技术应用于介质圆柱体逆散射问题,经过适当的训练,建立了介质圆柱体逆散射模型,并以此模型重构了已知探测范围内的介质圆柱体的半径、相对介电常数及电导率。

2.电磁逆散射问题描述

图1描述了一个典型的电磁逆散射物理系统。自由空间有一未知几何(如半径)和电磁(如相对介电常数、电导率)参数的目标,分布于有限区域V。一给定时谐电磁波Einc(r)(时谐因子ejωt)入射该散射体目标,由于电磁感应和极化作用,将在全空间激发二次场,即散射场Escatt(r)。可表示为

式中:r表示场点;r′∈V表示源点;k、k0分别表示介质和自由空间的波数;O(r)=k20[ε～r(r)-1]称为目标函数或对比度函数;E(r′)为介质体内的总场;

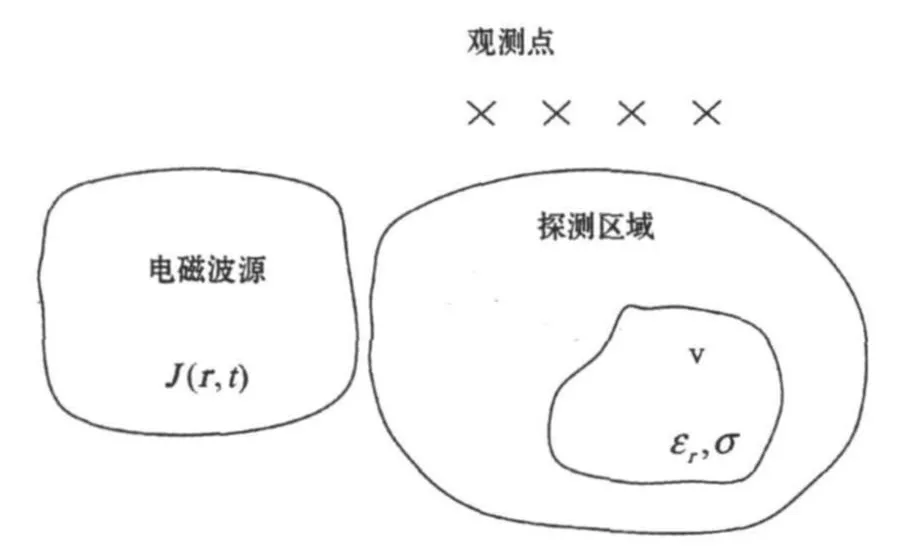
图1 电磁逆散射物理模型

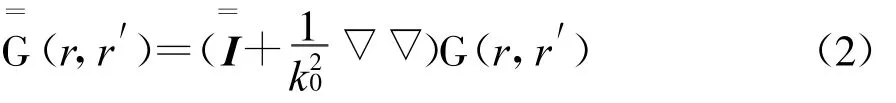
如果考虑二维散射体目标,在TM极化平面波的照射下,式(1)可简化为

从方程(1)、(3)可以发现,目标函数到散射场的映射关系是非线性的,这是由于二次散射源(散射体本身)各部分的相互作用造成的,因此,电磁逆散射问题呈现强烈的非线性特征。

逆散射问题的目标就是根据已有的观测点数据Escatt(r)获取散射体的位置、形状、电磁参数等信息。这种关系在数学上可表述为

式中:χ=[χi;i=1,…,P]=[r,εr,σ],P 是描述散射体的参数的个数。Escatt=[Esrcatt;r=1,…,R],R是观测点的个数。电磁逆散射问题可以重新被描述成一个回归问题,未知函数 Φ可以通过N个输入/输出(I/O)数据对来近似得到,(I/O)即为:{(χ)n,};n=1,…,N 。

3.用于回归估计的BP神经网络

人工神经网络具有强有力的学习能力,它不需要任何先验公式就可以通过学习或训练自动总结出数据间的函数关系,获得这些数据的内在规律,具有很强的非线性映射能力,适用于非线性问题的研究。因此,应用人工神经网络这一人工智能技术来研究电磁逆散射问题。

图2给出了文本所用的BP神经网络结构模型。它是一个三层前向神经网络,网络的输出在数学上可表示为

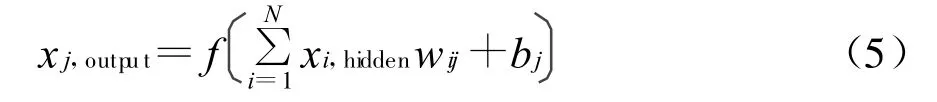
式中:x j是第j个神经元的输出;f是神经元的激活函数;N是隐含层神经元的个数;wij是隐含层中连结神经元j和神经元i的权重;bj是神经元j的阈值。

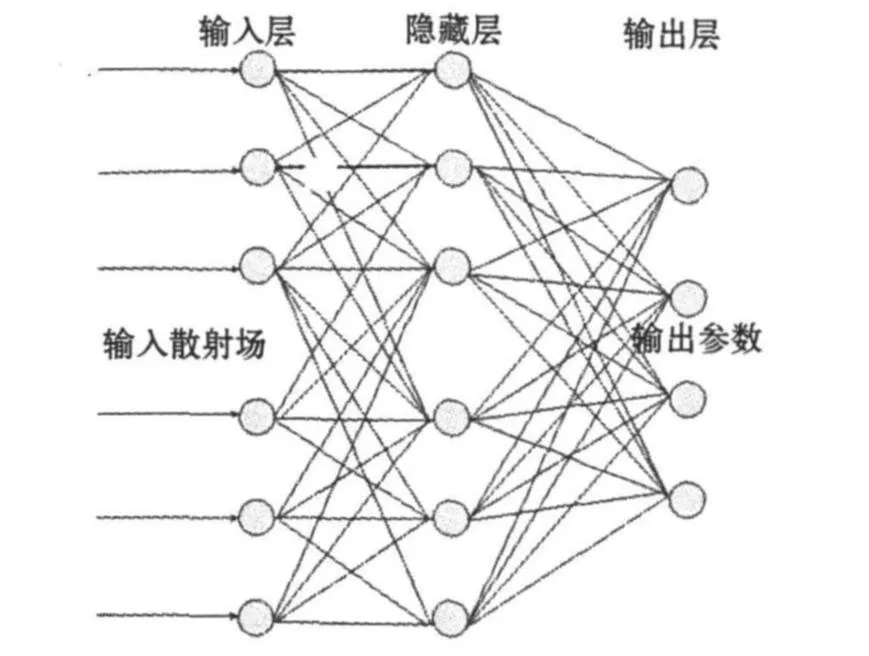
图2 电磁逆散射问题中的神经网络结构

输入层神经元的个数由电磁逆散射问题中所设置的散射场的接收点个数决定。比如,设置散射场的接收点是16个,如果以散射场的幅值作为训练样本信息,则输入层神经元的个数为16个;如果以散射场的幅值和相位作为训练样本信息,则输入层神经元的个数为32个。输出层神经元的个数由要反演的目标几何、电磁参数的个数决定。隐含层神经元的个数与网络性能的优劣密切相关,不同的隐含层神经元个数,对于同一个电磁逆散射问题,训练网络的时间不同,最后反演的精度也会不同,本文在后面将要用实例进行说明。

在本文的BP神经网络电磁逆散射模型中,隐含层神经元的激活函数采用sigmoid函数,考虑到训练样本多为非负数(散射场的幅值),所以最后采用对数形sigmoid函数作为隐含层神经元的激活函数。而输出层神经元的激活函数采用线性函数以展宽输出范围。

4.数值算例

4.1 介质圆柱体电磁参数重构

下面用BP神经网络方法来反演目标的相对介电常数和电导率。逆散射模型如图3所示,入射波频率1 GHz,在一边长为λ的正方形探测区域内有一半径R=λ/3=10 cm的二维介质圆柱体,假定其位于正方形的中心,其电磁参数未知。散射场的观

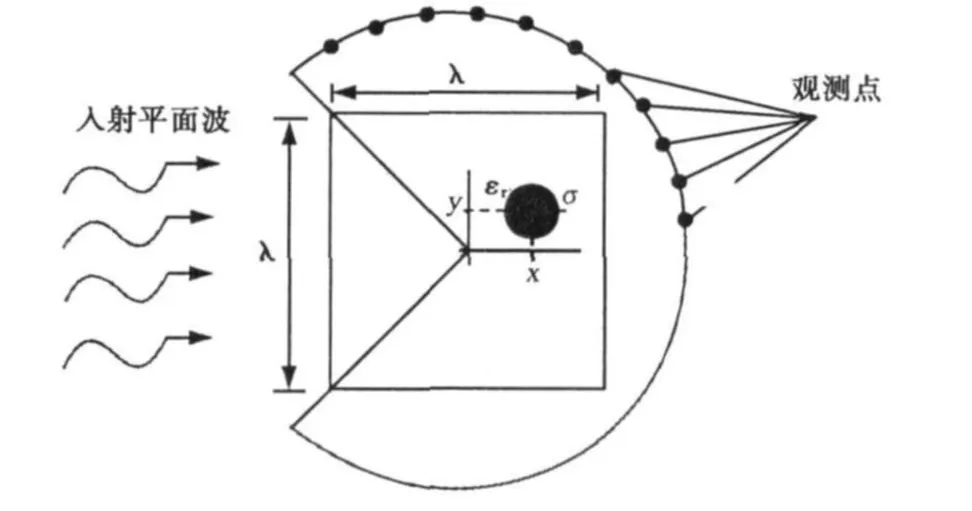
图3 二维介质圆柱体逆散射模型

测点数为12个,均匀地分布在以介质体中心为圆心、λ为半径的4πλ/3圆周上。训练样本数为315个,分别对应于15个不同的相对介电常数值(εr=1.5+0.25n,n=0,1,…14)和21个不同的电导率值(σ=10-3+0.05n(S/m),n=0,1,…,20),训练样本信息为观测点散射场的幅值,可用解析的方法得到[11]。显然,在这里,BP神经网络输入层神经元数为12,输出层神经元数为2。输出层神经元激活函数为线性函数,隐含层神经元激活函数为对数sigmoid函数。为了选取合理的中间隐含层神经元数,我们考虑以下三种BP网络结构:12-12-2、12-24-2、12-36-2。在相同的误差指标下,用 L-M 训练算法[12]对三种不同结构的BP网络进行训练,再用训练样本作为测试样本进行回归估计,通过计算它们的平均绝对误差(MAE),来比较三种不同结构的BP网络逆散射模型性能的优劣。结果见表1。三种网络结构的训练时间分别为24 s、27 s和35 s。

表1 三种不同结构BP网络逆散射模型误差比较

从表1可以看出,隐含层神经元数为24时对该实际问题是较为合适的。所以,我们采用结构为12-24-2的BP网络来重构相对介电常数和电导率。改变目标的电磁参数(不同于训练样本),用观测点上的相应散射场作为建立好的BP网络逆散射模型的输入,来重构介质圆柱体的相对介电常数和电导率。图4(a)、(b)分别给出了当 εr=1.55,1.80,2.05,2.30,2.55,2.76,3.05,3.30,3.80,4.30,4.55,4.9;σ=10-t(S/m),t=2.0,2.1,2.21,2.41,2.51,2.61,2.71,2.81,2.89,2.92,时的重构结果。

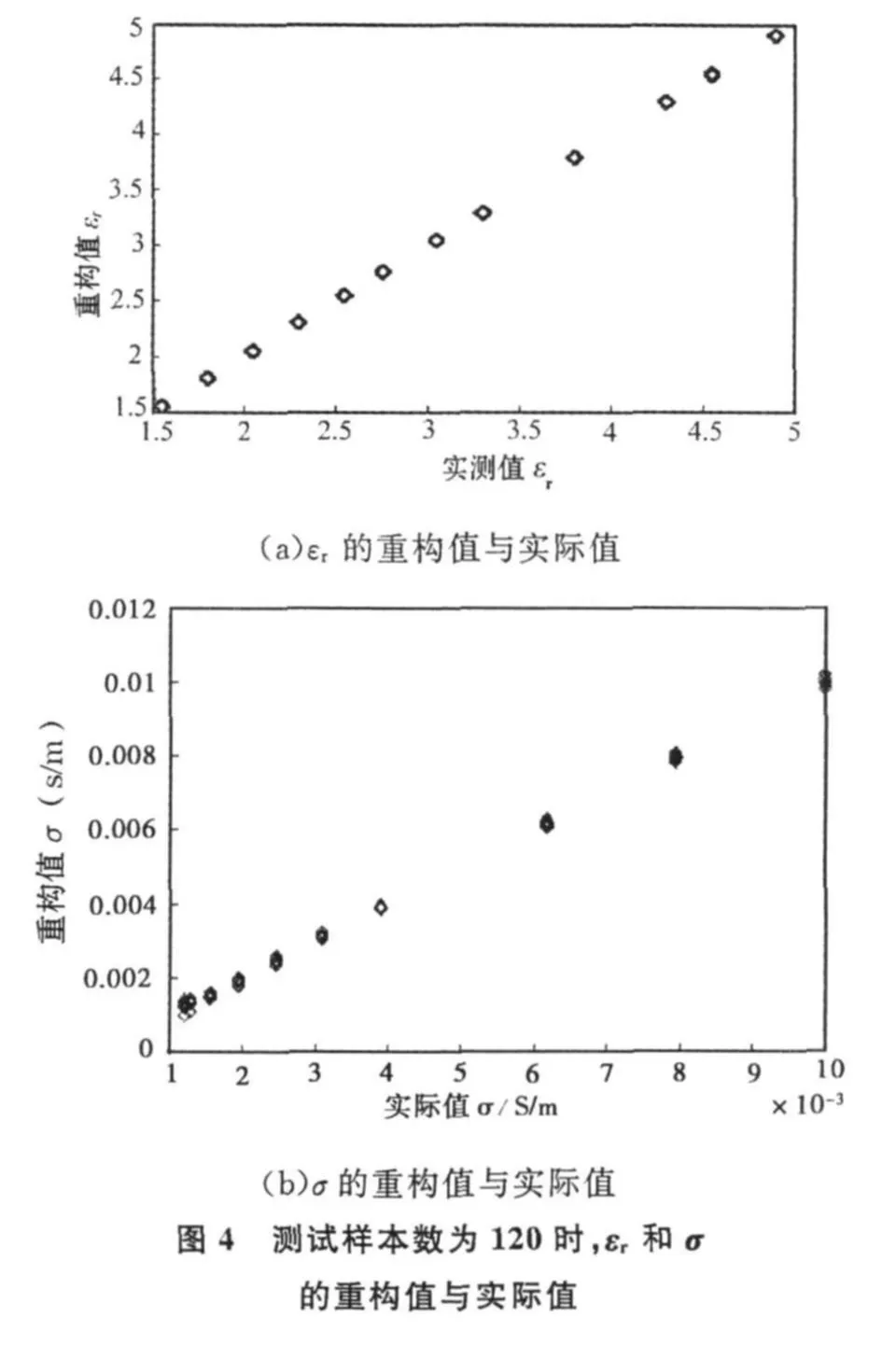
为了定量地说明重构的精度,分别计算重构结果的最大相对误差和平均相对误差

4.2 介质圆柱体几何、电磁参数重构

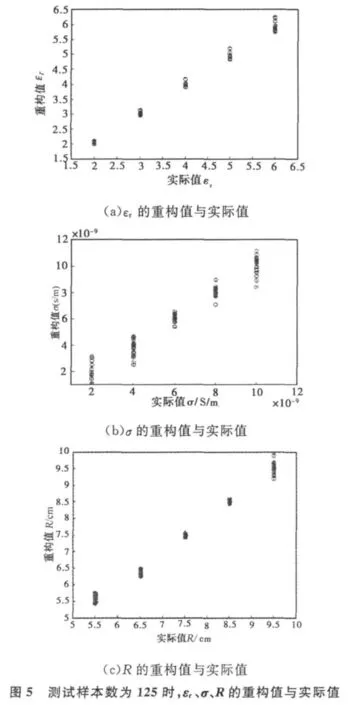
逆散射模型与算例1的图3相同,本算例中的反演参数分别为介质圆柱体的半径、相对介电常数及电导率。训练样本数为316个,分别对应于εr=1.5,2.5,3.5,4.5,5.5,6.5,σ=0.001,0.003,0.005,0.007,0.009,0.011(S/m),R=5.0,6.0,7.0,8.0,9.0,10.0(cm)。训练样本信息为观测点散射场的幅值,BP神经网络结构为12-24-3,采用L-M算法对训练样本进行训练并建立目标参数回归模型。训练时间为 38 s。图 5(a)、(b)、(c)分别给出了测试样本数为125个(εr=2.0,3.0,4.0,5.0,6.0,σ=0.002,0.004,0.006,0.008,0.010(S/m),R=5.5,6.5,7.5,8.5,9.5(cm))时相对介电常数εr、电导率 σ及半径R的重构结果。

5.结 论

利用BP神经网络对有耗介质圆柱体的半径、相对介电常数和电导率进行了重构。将原电磁逆散射问题转化成一个回归估计问题,通过神经网络对训练样本的学习,找出散射场与目标参数间的内在规律,建立相应的电磁逆散射模型,通过输入新的散射场信息,可实时反演出对应目标的半径、相对介电常数和电导率。这种基于机器学习的电磁逆散射方法克服了以往传统方法计算量大、耗时严重的缺点,且精度较高,为解决电磁逆散射问题提供了一条有效的途径。

[1] CHEW W C,WANG Y M.Reconstruction of two-dimensional permittivity distribution using the distorted Born iterative method[J].IEEE Transactions on M edical Imaging,1990,9(2):218-225.

[2] BELKEB K,ELISSALT M,GEFFRIN M.Newtonkantorovich and modified gradient inversion algorithm applied to ipswich data[J].IEEE Antennas and Propagation Magazine,1996,38(3):41-44.

[3] GARNERO L,FRANCHOIS A,HUGONIN J P,et al.Microwave imaging-complex permittivity reconstruction by simulated annealing[J].IEEE Trans.Microwave Theory Tech.,1991,39(11):1801-1807.

[4] CAORI S,PASTORINO M.Two-dimensional microwave imaging approach based on genetic algorithm[J].IEEE Trans.Antennas Propagat.,2000,48(3):370-373.

[5] 刘 波,高本庆,薛正辉,等.基于遗传算法在时域提取电磁参数的新方法[J].电波科学学报,2002,17(5):487-490.

LIU Bo,GAO Benqing,XUE Zhenghui,et al.A genetic algorithm for the evaluation of material parameters in time domain[J].Chinese Journal of Radio Science,2002,17(5):487-490.(in Chinese)

[6] HOOLESR H.Artificial neural networks in the solution of inverse electromagnetic field problems[J].IEEE Trans.Magn.,1993,29(2):1931-1934.

[7] DAWSON M S,FUNG A K,MANRY M T.A robust statistical based estimator for soil moisture retrieval from radar measurements[J].IEEE Trans.Geosci.Remote Sensing,1997,35(1):57-67.

[8] XIAO R,CHANDRASEKA R V.Development of a neural network based algorithm for rainfall estimation from radar observation[J].IEEE Trans.Geosci.Remote Sensing,1997,35(1):160-171.

[9] DAVIS D T,CHEN Z,TSANG L,et al.Retrieval of snow parameters by iterative inversion of a neural network[J].IEEE Trans.Geosci.Remote Sensing,1993,31(4):842-852.

[10] CHKRABARTI S,BINDAL N,THEAGHARAJAN K.Robust target classifier using artificial neural networks[J].IEEE Trans.Neural Networks,1995,6(3):760-766.

[11] BALANIS C A.Advanced Engineering Electromagnetics[M].New York:Wiley,1989.

[12] 程相君,王春宁.神经网络原理及其应用[M].北京:国防工业出版社,1995.