消磁绕组磁感应强度的延拓方法研究

杨明明 刘大明 刘胜道 连丽婷

(海军工程大学电气与信息工程学院,湖北武汉430033)

1.引 言

根据舰船的使命任务、航行区域以及防御水雷等级,不同的舰船将会设计不同的消磁绕组。当消磁绕组磁感应强度分布曲线不能良好地补偿舰船磁感应强度分布曲线时,要进行绕组安匝调整。如何快速准确获得在标准测量深度上的绕组磁感应强度(单个绕组区段的单位安匝的磁感应强度,称为绕组效率)成为进行绕组安匝调整的关键。受实际测量条件(水深和风浪等)的影响,实际测量时往往很难直接获得这类特定信息,需要从测量位置来推算标准位置的绕组磁感应强度。

目前,国内外对于消磁绕组磁感应强度延拓方法的研究极少,而对舰船磁感应强度的延拓方法主要有有限元法、积分方程法和磁体模拟法[1-4]。有限元和积分方程法都需要对舰船进行剖分,其剖分的合理性和疏密程度严重影响着延拓结果。对于形体复杂且庞大的舰船而言,剖分是非常复杂困难的,并且得到的方程组也将非常庞大,运算时间较长。常用的磁性模拟体主要有磁偶极子和磁椭球体,该方法易受人为经验的影响,稳定性和精度难以保证。边界积分方法只对求解区域边界剖分,使得形成的代数方程组维数大为减少,节约了计算成本,已广泛应用于磁源成相等领域[5]。本文在上述研究的基础上,从边界积分理论和等效原理出发,建立以有限平面为等效边界的边界等效源绕组磁感应强度延拓模型,采用Tikhonov正则化方法对模型进行求解以提高模型的稳定性,最后给出了实船实例计算结果。.

2.消磁绕组简介和磁场测量

消磁绕组是一组敷设在舰船内部的导线,在正常工作时,消磁绕组产生和舰船磁场大小相等、方向相反的磁场,从而抵消舰船的感应磁性和一部分舰船在磁性处理中没有消除的固定磁性。根据舰船的使命任务、航行区域以及防御水雷等级,不同的舰船将会设计不同的消磁绕组。典型消磁绕组的示意图如图1,其中XQ,YQ和ZQ绕组分别用来抵消舰船的纵向,横向和垂向感应磁性,ZF绕组用来抵消舰船在磁性处理中未消除的固定磁性。

绕组磁感应强度的测量分为两个步骤:①在消磁绕组未通电时,测量舰船磁感应强度B1;②接通消磁绕组电源时,测量在消磁绕组作用下的舰船磁感应强度B2。由于绕组通电产生的磁场较小,不会磁化舰船,所以绕组磁感应强度Bc可按下式计算

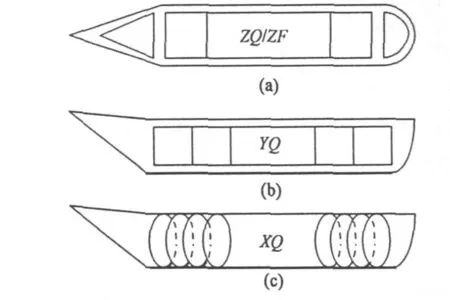
图1 消磁绕组示意图

消磁绕组的磁感应强度延拓的两种方案为:

方案一:在实际测量位置,按式(1)首先计算出在该位置的绕组磁感应强度(由于上述测量的两步骤能在较短的时间内完成,可以认为测量环境基本不变),再将绕组磁感应强度延拓到目标位置。

方案二:首先从实际的测量位置将舰船磁感应强度B1和在消磁绕组作用下的舰船磁感应强度B2延拓到目标位置,再按式(1)计算目标位置的绕组磁感应强度。

两种方案中的磁感应强度都可以视为铁磁物质和传导电流产生的,同时为了方便比较两种方案的延拓结果。因此,采用同一磁感应强度延拓模型。

3.基于有限平面的延拓模型

如图2,z=0的无限大平面将场域空间分成两部分V1和V,所有的磁源(包括铁磁物质和传导电流)都被限制在V1内。在z＞0的半空间区域内,没有电流分布(J=0),标量磁位φ满足拉普拉斯方程▽2φ=0。

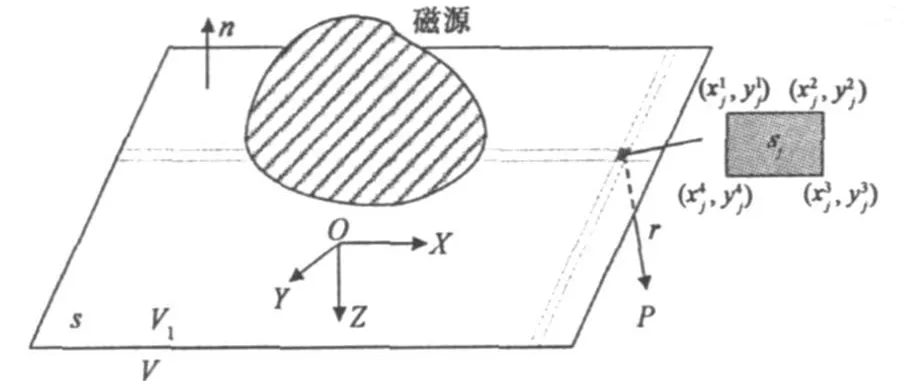
图2 场源和半空间场域

由文献[1][2],半空间区域V内的拉普拉斯方程边值问题的解为

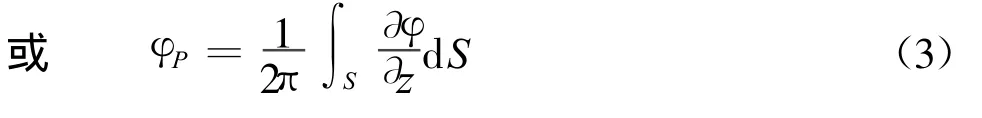
从式(2)和(3)可以看出:V 1内的磁源对V中任意位置的磁位φP的贡献可以用边界上的面积分来表示。如果已知边界面S上的等效磁源参数(φ或)后,可以由该式计算V中任何一点的标量磁位φP。在得到该点的φP后,通过求取该点的负梯度,并结合该点的磁导率μ,即可得到该点的磁感应强度。

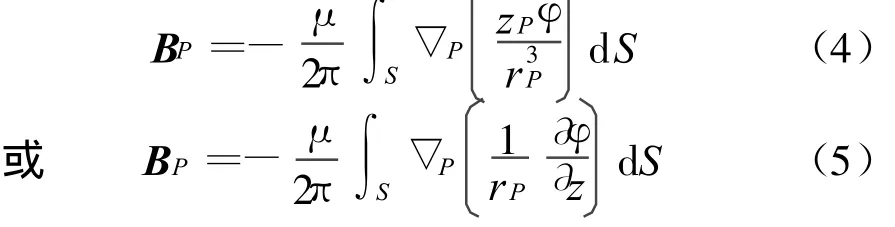
式中,偏微分是对边界上的源点坐标进行的,而梯度是对场点坐标进行的。不管采用式(4)或式(5)来计算场域内的磁感应强度,都具有同样精度[6]。考虑测量和积分计算的简便性,一般采用式(5)来求解场域中的磁感应强度。在实际使用时,还需要进行以下的两个处理步骤:①边界面应取有限边界面(一般取2倍船长,2倍船宽的矩形为边界面,下节的实船实例也证明了有限边界面的有效性);②将有限边界面划分为N个离散单元,当各离散单元足够小时,其磁性参数可以看作常数。此时式(5)可离散化为

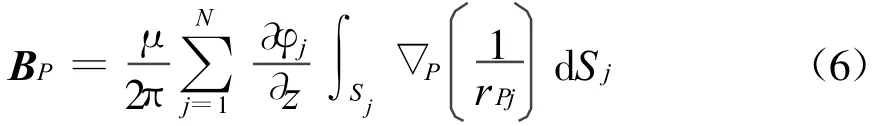
这就是边界上的等效磁源参数与无磁区域V中的磁感应强度的正演关系。如果我们能够获得z＞0的半空间内某个平面z c上的磁感应强度测量值,则可以直接由式(6)计算z＞z c的区域内任何位置的磁感应强度,该方法称为“大平面换算法”。由于该方法对测量环境要求较高(如测量面应该足够大;为了挑选合适换算的测量点,测量点布置尽量密集、规律化和程序化),所以其使用受到一定的限制[1]。

如果在区域V内测量得到一组磁场感应强度后,利用式(6)反演出边界上的等效磁源参数,则可以利用这组等效磁源参数计算区域V内任意位置的磁感应强度。由于在舰船磁场延拓的实际工程中,常采用单分量传感器进行检测,故一般只能得到磁感应强度数据的z分量值,且对舰船磁场的评估和处理目前也只考虑z分量值,所以基于z分量的延拓模型更加具有实用性。

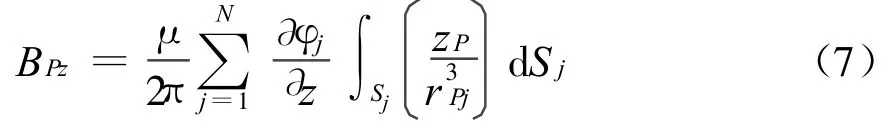
式(7)写成矩阵形式可表示为AX=b,其中X为磁性参数组成的列向量,b为测量值组成的列向量,系数矩阵A是将等效源磁性参数和测量值联系起来的线性观测矩阵,矩阵元素的值与场点P i和边界单元Sj有关,其积分与单元的具体形状密切相关。本文采用图2中的矩形单元,积分的具体解析表达式见下面的式(8)。

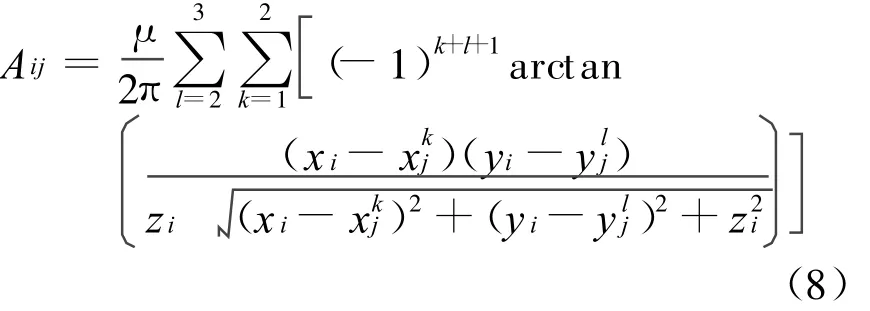
式中:i表示第i个测量点;j表示第j个离散单元;xkj,ylj分别表示第j个单元的第k个节点的横坐标和第l个节点的纵坐标;(xi,yi,zi)为第i个测量点的三维坐标。

作为延拓磁感应强度所需的第一个步骤,我们完成了延拓模型的分析。延拓的具体过程可以描述为:在某些特定位置,得到磁场感应强度的一组有效测量数据,求解方程组AX=b反演得到边界上一组等效磁性参数后,再利用式(7)计算其他位置的磁场感应强度。

4.Tikhonov正则化求解逆问题

与微波成像计算中离散化所得到的线性方程组类似,由上节模型导出的方程组也常呈现较严重的病态特性,测量数据以及计算过程的微小误差就会造成结果的巨大偏离[7]。出现这种现象的主要原因有:1)形成方程组的过程中,每个边界单元内的磁位的法向导数是利用其在该单元中心的法向导数来近似的。为了保证近似的有效性,需要将边界划分较多的单元,单元的增多,会使得形成的方程组的系数矩阵的列相关性增强,系数矩阵的条件数增大。当测量点间距较小时,这种现象尤其突出。2)计算机在存储和计算过程中的有限字长效应,也会加剧逆问题模型的病态特性。而我们在求解方程组时,通常按线性最小二乘来求解,即求解法方程组

若方程本身是病态的,则法方程会更加地病态[8]。所以我们在求解逆问题模型参数时,需要借助其他手段。国内外很多学者都对这类病态问题进行了研究,这些研究表明TSVD和Tikhonov正则化等方法可以较好的处理逆问题中由系数矩阵病态特性而造成的结果的不稳定性[7-12]。因此,采用Tikhonov正则化方法对方程组进行求解。

假设实际测量过程中测量误差为ξ,理想情况下磁感应强度测量值为c,则有b=c+ξ,AX=c+ξ.对系数矩阵进行奇异值分解A=USVT,则经正则化处理后,方程组的解可以表示为

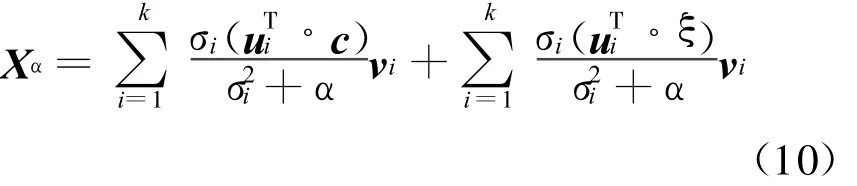
分析式(10)可知,Tikhonov正则化方法的实质是在奇异值上叠加一个极小的正实数α(正则化参数),抑制异常小的奇异值σi对噪声的放大作用,达到正则滤波的目的。从式(10)我们还可以看出,若正则化参数α选取较大(过正则化),则Xα与真解差别较大,模型的精确性降低;若正则化参数α选取较小(欠正则化),则无法抑制对噪声的放大作用,模型的稳定性下降。所以恰当的正则化参数需要在模型的精确性和稳定性之间做出一个合适的折中。

在计算模型参数的过程中,通常所拥有的先验信息较少,尤其是无法预知测量数据中的噪声水平,采用后验选取法确定正则化参数具有优势。后验选取方法主要有 L曲线法,交叉校验(cross validation,CV)和广义交叉校验(generalized cross validation,GCV)。这三种方法直接从测量数据出发,通过预解方程组来确定正则化参数,而不需要先验信息,适合本文中逆问题的求解。本文采用GCV函数来选取正则化参数,定义如下的函数

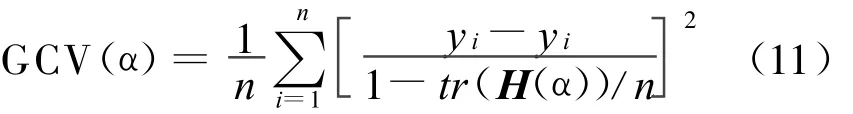
式中:H(α)=A(ATA+αI)-1AT;y=H(α)y;tr(H(α))为H(α)的迹。使函数GCV取得最小值的就是由广义交叉校验所求得的正则化参数。图3和图4分别给出了两种延拓方案的典型GCV函数曲线。

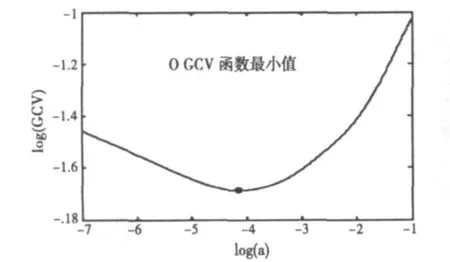
图3 延拓方案一的典型GCV曲线

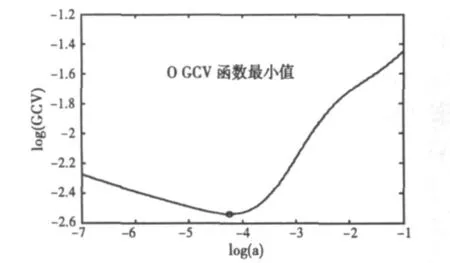
图4 延拓方案二的典型GCV曲线

5.实船实例分析

在某新建的现代化大型消磁站中,按绕组效率测量步骤,以5 m为间距采集得到某型舰船在27×4点阵列上的舰船磁感应强度z分量。如图5所示,测量平面高度分别为 z1=15.872 m和 z2=20.872 m,测量范围分别为130 m×10 m(z1)和130 m×13 m(z2)。有限边界取为2L×2B的矩形(L和B分别为船长和船宽),整个边界共划分为24×4个单元。分别利用z1(z2)平面上的测量数据,建立相应的磁场模型,并由模型计算得到了各绕组在z2(z1)平面的磁感应强度。定义平均相对误差其中Bm和Bc分别为磁感应强度的测量值向量和推算值向量,B m max为磁感应强度测量值的最大值,M为向量维数[13]。表1给出了各绕组磁感应强度的延拓结果。

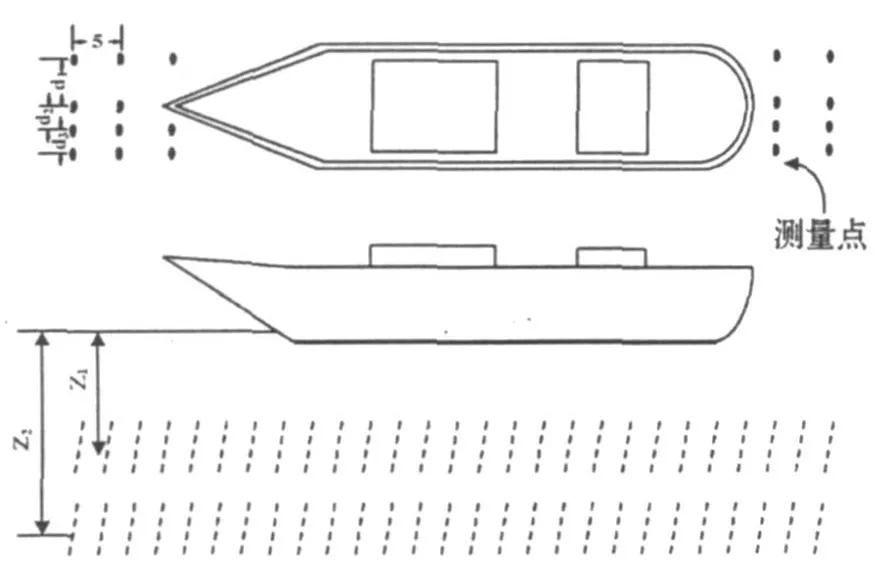
图5 测量示意图(z1:d 1=5 m,d 2=3 m和d3=2 m;z2:d1=7 m,d 2=2 m和d3=4 m)

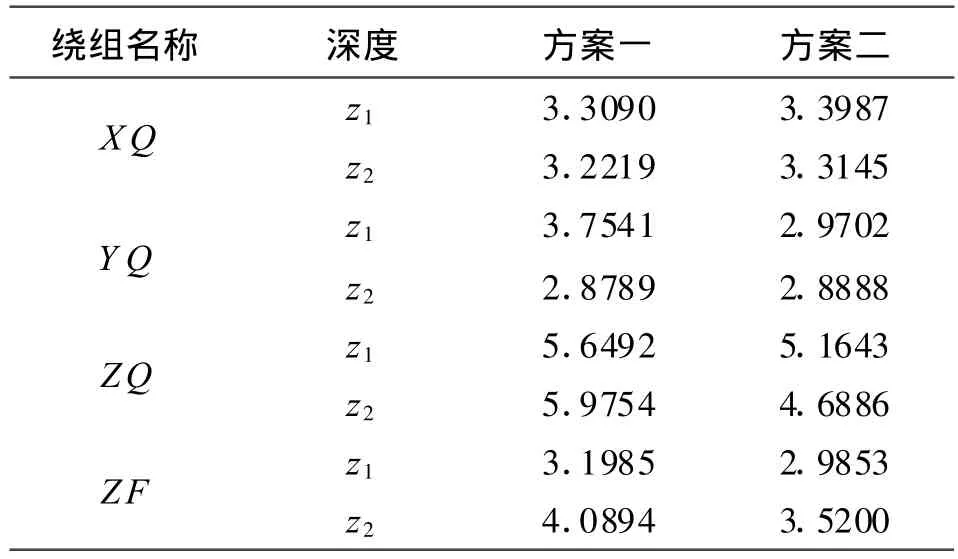
表1 各绕组磁感应强度延拓结果

从表1中可以看出:除z1深度的YQ绕组和z 2深度的ZQ绕组磁感应强度平均相对误差(ER)差别较大(分别为0.78%和1.29%)之外,其他情况下,两种方案的平均相对误差的最大差别都控制在0.5%的范围内;消磁绕组磁感应强度延拓的两种方案都具有较高的精度,能够满足实际的需要。

图6和图7分别给出了近场到远场及远场到近场的推算值与测量值的对比曲线(由于篇幅的原因,只画出各绕组部分位置的磁感应强度比较图,其他位置有同样的性质)。

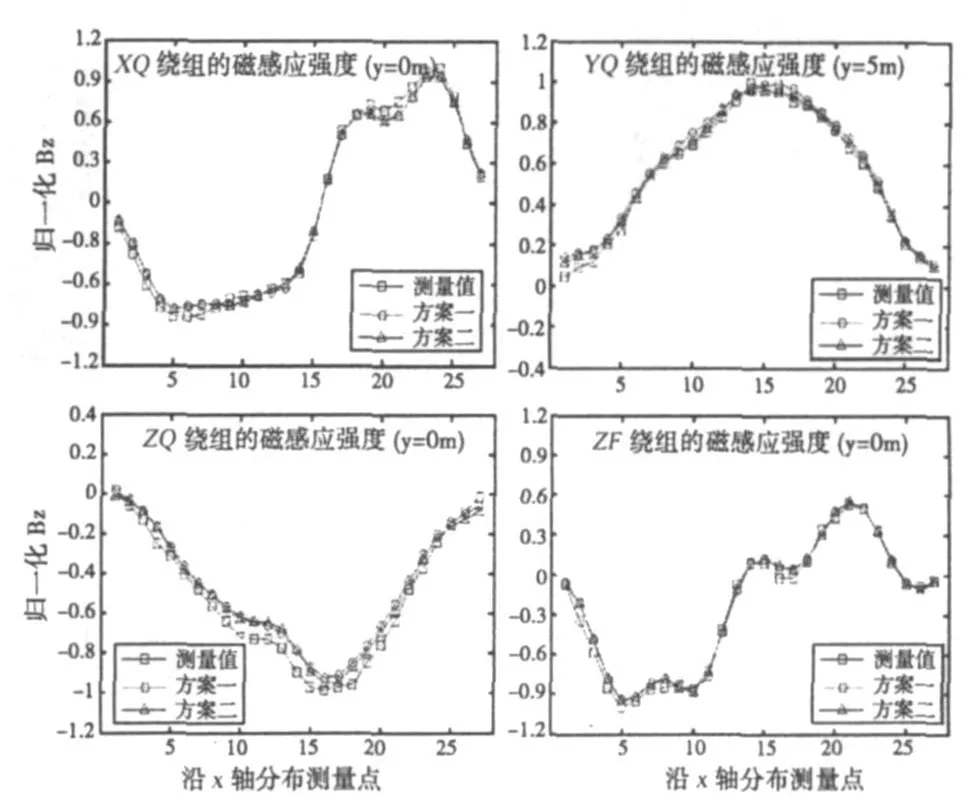
图6 z1深度,测量值和推算值比较图

从图中可以看出:(1)由近场推算远场时,XQ、YQ和ZF绕组磁感应强度z分量的推算误差均可控制在6%以内,ZQ绕组磁感应强度z分量较大约为9.7%;(2)从远场推算近场模型误差稍大,XQ、YQ和ZF绕组均可控制在10%以内,ZQ绕组仍然偏大为12.7%。ZQ绕组延拓误差偏大的原因可能是测量误差造成的。

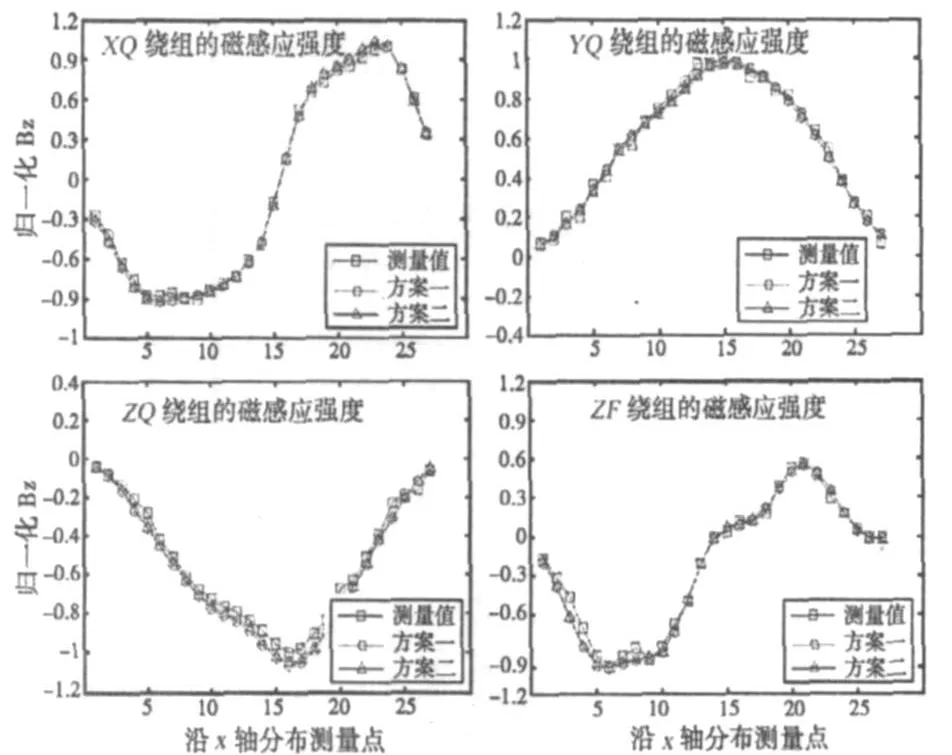
图7 z2深度,测量值和推算值比较

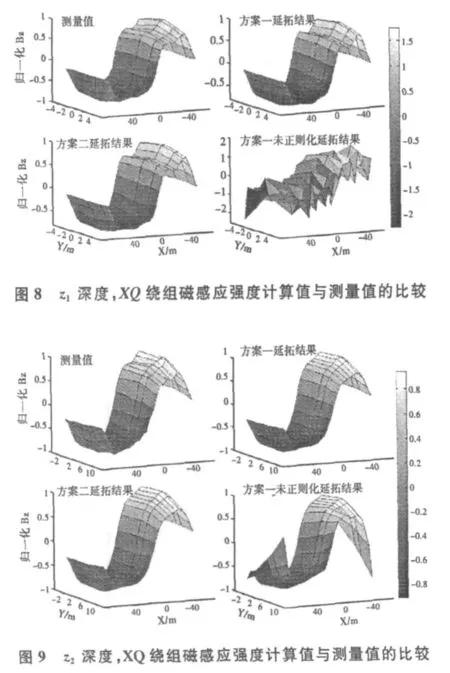
图8 和图9分别给出了经正则化处理和未经正则化处理两种情况下,XQ绕组磁感应强度z分量在两个不同深度上的推算值与测量值的对比曲面。由于两种方案的延拓结果差别较小,因此在未经正则化处理的情况下文中只给出了采用方案一的延拓结果;同时限于篇幅的原因,文中仅给出了XQ绕组的延拓结果,其他绕组磁感应强度具有同样的性质。从图8和图9可以看出,Tikhonov正则化技术不但提高了延拓精度,而且增强了模型的稳定性。

6.结 论

研究了基于Tikhonov正则化方法的绕组磁感应强度延拓方法,分析了两种不同延拓方案对延拓结果的影响。与基于传统等效源法的延拓技术相比,具有以下优点:1)该方法有效消除了传统等效源法中人为因素对建模过程的影响,提高了模型的通用性。2)针对实际测量中存在的误差,借助 Tikhonov正则化方法求解,大大提高了模型的稳定性,降低了实际工程中测量误差给建模结果带来的扰动,更具有实际工程应用价值。实船实例表明:绕组磁感应强度延拓精度满足舰艇消磁技术要求,可用于工程实际。

[1] 周耀忠,张国友.舰船磁场分析计算[M].北京:国防工业出版社,2004:135-153.

ZHOU Yaozhong,ZHANG Guoyou.Theanalysis and caculation of the magnetic field of ships[M].Beijing:Press of National Defence Industry,2004:135-153.(in Chinese)

[2] 周国华,肖昌汉,刘胜道,等.一种舰艇磁隐声中磁场推算的新方法[J].兵工学报,2009,30(7):951-956.

ZHOU Guohua,XIAO Changhan,LIU Shengdao,et al.A new magnetic field extrapolation method in magnetic silencing of ships[J].Acat Armamentarii,2009,30(7):951-956.(in Chinese)

[3] 王金根,龚沈光,刘胜道,等.磁性目标的高精度建模方法[J].海军工程大学学报,2001,13(3):49-52.

WANG Jingen,GONG Shenguang,LIU Shengdao.High accurancy method for modeling magnetic object[J].Journal of Naval University of Engineering,2001,13(3):49-52.(in Chinese)

[4] 金守强.电磁场边值问题的解法及其特点[J].沈阳工业大学学报,2001,24(2):130-131.

JIN Shouqiang.Methods and particulars for solving boundary problem of electromagnetic field[J].Shenyang College for Staff&Workers,2001,24(2):130-131.(in Chinese)

[5] 钱祖平,丁振宇,洪 伟.边界元法与遗传算法应用于导体柱的成像[J].电波科学学报,2000,15(1):49-54.

QIAN Zuping,DING Zhenyu,HONG Wei.Application of GA and BEM to imagining of conductor cylinder[J].Chinese Journal of Radio Science,2000,15(1):49-54.(in Chinese)

[6] 李忠元.电磁场边界元素法[M].北京:北京工业学院出版社,1987:244-247.

LI Zhongyuan.Magnetic boundary element method[M].Beijing:Press of Beijing Industry College,1987:244-247.(in Chinese)

[7] 陈 星,黄卡玛,袁 渊,等.微波生物医学成像算法中的病态及伪逆问题[J].电波科学学报,2000,15(1):65-69.

CHEN Xing,HUANG Kama,YUAN Yuan,et al.The discussion of pesudoinversion and ill-posedness in the caculation of microwave biomedical imagining[J].Chinese Journal of Radio Science,2000,15(1):65-69.(in Chinese)

[8] David Kincaid,Ward Cheney.Numerical Analysis:Mathematics of Scientific Computing[M].3rd ed.Beijing:China Machine Press,2003:279-280.

[9] 郭成豹.基于积分方程法和奇异值分解的舰船磁场建模技术研究[D].武汉:海军工程大学,2007:56-85.

GUO Chengbao.Study On Ship Magnetic Field M odelling Technique Based on Integral Equation Method and Singular Value Desomposition[D].Wuhan:Naval University of Engineering,2007:56-85.(in Chinese)

[10] 徐张明,沈荣瀛,华宏星.奇异值分解(SVD)和Tikhonov正则化方法在振速重建中的应用[J].上海交通大学学报,2002,36(6):834-838.

XU Zhangming,SHEN Rongying,HUA Hongxing.Vibrating velocity reconstruction using singular value decomposition and Tikhonov regularization method[J].Journal of Shanghai Jiaotong University,2002,36(6):834-838.(in Chinese)

[11] 黄卡玛,赵 翔.电磁场逆问题及其应用[M].北京:科学出版社,2005:37-41.

HUANG Kama,ZHAO Xiang.Inverse problems of electromagnetic field and their uses[M].Beijing:Press of Science,2005:37-41.(in Chinese)

[12] ENGL H W.Discrepancy principles for Tikhonov regularization of ill-posed problems leading to optimal convergence rates[J].J.Optim.Theory.Appl.,1987,52(2):209-215.

[13] 瓮行泰,曹梅芬.潜艇感应磁场的三维有限元计算研究[J].上海交通大学学报,1994,28(5):69-76.

WENG Xingtai,CAO Meifen.A resarch on the caculation of the induced magnetic field of a submarine[J].Journal of Shanghai Jiaotong University,1994,28(5):69-76.(in Chinese)