基于FFT并二次修正的Rife频率估计算法

谢 胜,陈 航,于 平

(1.西北工业大学航海学院,陕西西安 710072;2.91388部队,广东湛江 524022)

0 引言

在鱼雷攻击潜艇过程中,确定鱼雷引信的炸点位置非常重要,这对于目标毁伤效果有直接的影响。工作区域主要在近场区的鱼雷主动声引信,回波的体目标效应明显,引信接收到的信号为多个散射点回波信号的组合,回波信号的频谱不再是单一的频率,而是占据一定谱带的、离散且随时间变化的频谱[1-2]。为高精度地提取潜艇目标回波各亮点多普勒频率信息以便完成后续运动参数的估计,国内外学者提出了一些快速高精度频率估计的方法[3-4]。

基于DFT的谱分析法采用快速算法(FFT),运算速度快,特别适合实时信号处理,但由于利用FFT进行谱分析只能对有限多个样本进行处理,不可避免地存在由于时域截断产生的能量泄漏,使谱峰值变小、精度降低,即经FFT得到的离散频谱其幅值、相位和频率都可能产生较大的误差,于是人们又提出了基于FFT的各种插值算法。目前常用的基于FFT插值算法有:KAY法[5],双线幅度 Rife法[6],结合幅度与相位的双线Quinn法[7]等。Rife法和Quinn法由于算法简单、计算量小,在工程实际中得到广泛应用。文献[8]分析了Rife法和Quinn法的频率估计方差,指出:当信号频率在接近DFT量化频率中心区域时,Rife法和Quinn法标准差接近理论频率估计方差下限;而当信号频率接近DFT量化频率且信噪比较低时,两者估计误差较大。对比Quinn法和Rife法的估计方差可知:在同等条件下Quinn法比 Rife法具有更小的估计方差。文献[9]分析Rife法的性能,提出了一种修正 Rife(MRife)算法,通过对信号进行频移,解决了当信号频率位于量化频率点附近时估计精度降低的问题,在适当的信噪比(0 d B以上)时,M-Rife算法在整个频段上频率估计均方误差十分接近克拉美罗限CRLB;但当信噪比较低且当信号频率位于DFT量化频率附近时,M-Rife算法可能出现频移方向出错而导致估计误差增大,需要进行二次修正。

针对M-Rife算法在低信噪比条件下估计性能下降的问题,本文提出一种基于FFT并二次修正的Rife频率估计算法。

1 M-Rife算法

加性高斯白噪声污染的信号表示为:

式中:a,f c,φ0分别为振幅、频率和初相;Δt为采样间隔;N为样本数;w(n)为实部和虚部相互独立的、方差为2σ2的零均值复高斯白噪声。

Rife算法公式可表示如下:

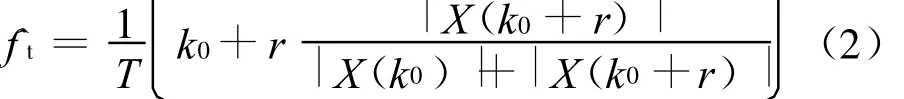
令Rife算法插值项为:

式中,|X(k0)|为X(n)的FFT最大谱线的幅值,|X(k0+r)|为FFT次大谱线的幅值,k0为FFT最大谱线位置。当|X(k0+1)|≤|(X(k0-1)|,r=-1;反之r=1,T=N◦Δt。当信号频率位于FFT量化频率附近时,Rife算法在确定次大谱线时易受噪声干扰发生插值方向错误,估计的误差将可能大于DFT算法。

M-Rife算法建立在Rife算法基础上,利用了Rife算法当信号频率位于FFT两相邻量化频率中心区域估计精度高的特点。其实现原理是:首先在对信号样本作FFT基础上用Rife算法进行频率估计,如果估计出的频率位于FFT两相邻量化频率中心区域即|A|∈(ε,λ),其中0≤ε≤λ≤1/2,则以此估计值作为最终的频率估计结果,否则对原始信号进行频移p个量化单位以使信号频率位于FFT两相邻量化频率中心区域,再用Rife算法估计频率。M-Rife算法在对信号进行频移之前根据式(2)中r取值来确定频移方向,若r=-1,向左频移,反之向右频移。也就是说M-Rife算法根据次大谱线位置来确定频移方向。当信噪比较低且当信号频率位于DFT量化频率附近时,可能出现频移方向出错而导致估计误差增大。M-Rife算法流程图如图1所示。

图1 M-Rife算法流程图Fig.1 flow chart of M-Rife algorithm

2 基于二次修正的Rife算法

针对M-Rife算法在低信噪比条件下估计性能下降的问题,提出一种基于FFT并二次修正的Rife频率估计算法。由于利用FFT进行谱分析只能对有限多个样本进行处理,不可避免由于时域截断产生的能量泄漏导致FFT得到的离散频谱其幅值、相位和频率都可能产生较大的误差。因此,改进算法首先通过计算机仿真方法搜索特定频段的最佳修正因子m opt以对FFT最大谱线位置号进行初步修正。基于FFT估计的信号频率可表示为 f=(k0+δ)◦Δf,式中δ∈[-0.5,0.5],k0为FFT最大谱线位置号,Δf为FFT的频率分辨率。假设被估计频率在特定的频段为均匀分布,在该频段内均匀选取N个频率点,按照式(1)定义的输入信号作FFT,根据公式f=(k0+δ)◦Δf估计频率,每个频率点做1 000次蒙特卡罗仿真。以估计频率的均方根误差最小为准则求出各频率点的最佳修正因子δi,然后将N个最佳修正因子δi进行平均处理得到该频段内最佳修正

量m opt:

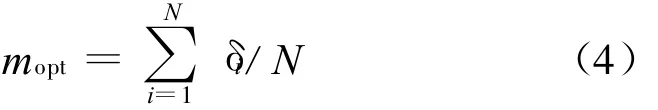
在求得mopt的基础上校正的Rife法公式可表示为:

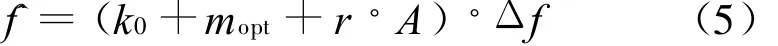
前面分析已指出,M-Rife算法在Rife法基础上根据次大谱线位置来确定频移方向。当信噪比较低且当信号频率位于DFT量化频率附近时,可能出现频移方向出错而导致估计误差增大。与M-Rife算法不同,改进算法在对原始样本进行频移之前,采用FFT最大谱线左右两侧谱线的相位信息即Quinn法来确定频移方向,并且对原信号样本作频移后用校正的Rife法公式估计频率时以Quinn法估计结果来确定插值方向。

Quinn算法利用FFT主瓣内的次大谱线与最大谱线系数复数值之比的实部进行频率估计。Quinn算法原理描述如下:设FFT最大谱线位置号k0,则k0-1,k0+1分别位于最大幅度值的两侧,且其中一个为次大值。定义:

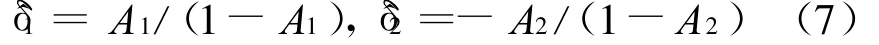
于是Quinn算法的频率插值项可表示为:

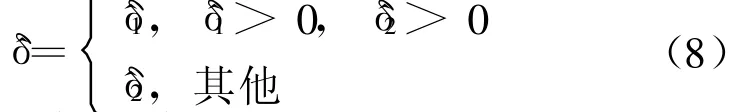
改进算法的流程图如图2所示。

图2 改进算法流程图Fig.2 Flow chart of the improved algorithm

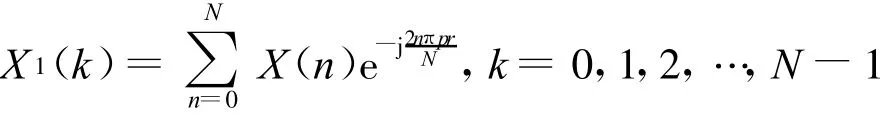
式中,p(p＞0)为频移量,对新样本作FFT,由式(3)求出 A′,然后将 A′减去p 得到A=A′-p,最后将k0+m opt和A代入校正的Rife法式(5)得到最终的频率估计值。此时式(5)中r取值由Quinn法估计结果来确定,这与M-Rife算法是不同的。

其原理是:若估计的频率位于FFT两相邻量化频率中心区域即|A|∈(ε,λ),则用m opt对k0进行修正,得到k0+mopt,再与A一起代入校正的Rife法公式(5)估计频率,此估计值作为本次实测样本最终的频率估计值(此时公式r取值与M-Rife算法同);否则若估计的频率不位于FFT两相邻量化频率中心区域,则根据 Quinn 法公式(6)、(7)计算 ^δ1,^δ2 值并作判断 :若＞0,＞0,令 r=1,向右频移 ;否则令r=-1,向左频移。频移得到新样本为:

3 仿真分析

在Matlab中对上面介绍的改进算法作了Monte Caro仿真。按照式(1)定义的输入信号,相关参数设置如下:输入信噪比SNR=a2/2σ2,信号初始相位φ0取[0,2π]区间均匀分布的随机数,噪声均值为0、方差σ2=0.5。FFT量化频率的中心区域为[0.3,0.5],频移量 p取 0.3。对每个频率点作1 000次Monte Caro仿真。

3.1 不同信号频率的估计误差

图3为鱼雷攻击目标示意图,鱼雷与目标多普勒频移:f d=2f c V/C,其中V为鱼雷与目标连线方向相对速度,C为海水的声速,f c为鱼雷声引信载频。取脱靶量d=2 m,鱼雷与目标在水平方向初始距离为X0=30 m,鱼雷速度V TS=25 m/s,C=1 500 m/s,信噪比SNR=3 dB,声引信载波频率f 0=350 kHz,采样频率为 f s=1.4 MHz,信号样本长度N=256,则FFT的频率分辨率为Δf=1 376.2 Hz。假定点目标固定不动,则多普勒频移范围为[-15 000 Hz,15 000 Hz]。

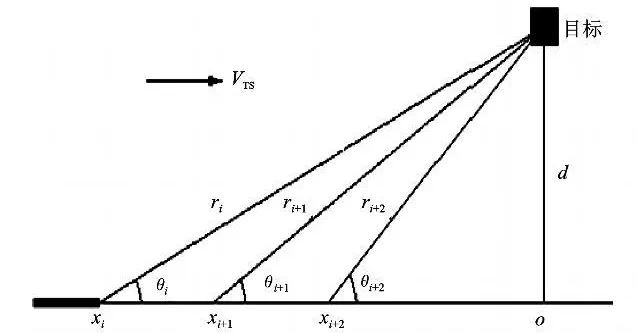
图3 鱼雷攻击目标示意图Fig.3 Torpedo attacks taget

图4 为用改进算法估计的鱼雷与目标多普勒频移图,其中图4(b)、(c)分别为对图4(a)左右两半部分曲线进行局部放大的效果图。从图4可看出,改进算法在整个频段范围内频率估计均值都非常接近真实值,估计多普勒频移曲线与真实多普勒频移曲线非常吻合。

图4 改进算法估计多普勒频移曲线图Fig.4 The Doppler frequency shif t curveestimated by the improved algorithm

表1给出了鱼雷与目标水平距离分别为6 m、5 m、…、0 m,信噪比为3 dB,样本长度 N分别为256、512改进算法的估计均方根误差。从表1可知,当N=256时改进算法估计均方根误差不到FFT频率分辨率Δf=1 376.2 Hz的1%,估计精度很高。当N=512时,估计均方根误差最大值不大于36 Hz。可见改进算法在炸点附近的频率估计精度能够满足反潜鱼雷主动声引信提取目标回波各亮点多普勒频率的应用要求。

表1 SNR=3 d B,N=256、512,X=6 m、5 m、…、0 m条件下改进算法估计均方根误差(RMSE)Tab.1 RMSE of the improved algorithm for SNR=3 dB,N=256,512,X=6 m,5 m,…,0 m

3.2 与M-Rife算法性能比较

图5给出了与文献[9]相同仿真参数条件下改进算法与M-Rife法的估计均方根误差。图5(a)—(c)细实线分别取自文献[9]表2—4中当信噪比分别6 d B,0 d B,-3 dB时11个频率点估计均方根误差数据作图而得到,粗实线表示改进算法的均方根误差。从图5(a)、(b)可看出,当信噪比SNR在0 dB以上时,改进算法和M-Rife法的均方根误差均十分接近CRLB,两者估计性能相当;而当SNR=-3 d B时,改进算法的估计稳定性要明显好于MRife算法。这是由于在低信噪比时且当信号频率接近于FFT量化频率时M-Rife法易因频移方向错误导致估计误差偏大,而改进算法利用了相位信息来判断频移方向,降低了频移方向的错误概率,估计误差得到有效控制。显然,在低信噪比条件下,改进算法估计性能要优于M-Rife法。

图5 当SNR=6 d B,0 d B,-3 d B时,改进算法和M-Rife算法的均方根误差Fig.5 RMSE of the improved algorithm and M-Rife for SNR=6 d B,0 d B,-3 d B

3.3 不同信噪比条件下估计误差

为检验改进算法在不同信噪比条件下的估计性能,选取一个接近FFT量化频率的频率点 f 1=f 0+0.05Δf进行仿真,取 f 0=50 MHz,采样频率为fs=200 MHz,N=256,则FFT频率分辨率Δf=781.2 k Hz。信噪比区间为[-8 dB,8 dB],间隔为1 d B,在每个SNR点作1 000次蒙特卡罗仿真,估计频率方差下限为:

图6给出了改进算法在不同信噪比条件下的均方根方差与CRLB比较。

从图6可看出,尽管被估计信号频率非常接近FFT量化频率,但改进算法在很宽信噪比范围内均方根方差都十分接近CRLB。例如当SNR=-8 d B时,改进算法的均方根误差约为CRLB的1.14倍。当SNR=-3 d B时,改进算法的均方根误差约为CRLB的1.09倍;而在同等条件下M-Rife法其均方根误差达到CRLB的1.4倍。随着信噪比提高,改进算法的均方根误差越来越接近CRLB。可见,改进算法比M-Rife法具有更宽信噪比门限。综上所述,改进算法整体性能要优于M-Rife法。

图6 改进算法在不同信噪比条件均方根误差Fig.6 RMSE of the improved algorithm in different SNR

4 结论

针对M-Rife算法在低信噪比时估计性能下降问题,本文提出了一种基于FFT并二次修正的Rife频率估计算法。该算法首先利用修正因子对FFT最大谱线进行修正,然后用校正的Rife法公式估计频率。若被估计信号频率接近于FFT量化频率,则对信号进行频移以使信号频率位于两相邻量化频率的中心区域,再用校正的Rife法公式估计频率。频移方向由Quinn法来确定。计算机仿真结果表明:改进算法不仅在整个被估计的频段内具有较高估计精度,均方根误差接近于CRLB,而且具有低信噪比门限,整体性能要优于M-Rife法。改进算法计算量不大,便于硬件实现,具有较高工程应用价值,能够满足反潜鱼雷主动声引信提取目标回波多普勒频率的应用要求。

[1]Hao L,Paknys R.Comparison of near-field scattering for finite and infinitiearrays of parallel conducting strips TM incidence[J].IEEE Transactions on Antennas and Propagations,2005,53(11):3 735-3 740.

[2]Yu D,Fu D.A novel method of plannar near-field scattering measurements[C]//IEEE Internatinal Symposium on Microwave,Antenna,Propagation and EMC Technologies for Wireless Communications.USA:IEEE,2005:483-486.

[3]丁康,谢明.离散频谱三点卷积幅值修正法的误差分析[J].振动工程学报,1996,9(1):92-98.

[4]段虎明,秦树人,李宁.离散频谱的修正方法综述[J].振动与冲击,2007,26(11):138-145.DUAN Huming,QIN Shuren,LI Ning.Review of correction methods for discrete spectrum[J].Journal of Vibration and Shock,2007,26(11):138-145.

[5]Steven Kay.A Fast and Accurate Single Frequency Estimator[J].IEEE Transactions on Acoustics Speech and Signal Proeessing,1989,37(12):56-62.

[6]Rife D C,Vincent G A.Use of the Discrete Fourier Transform in the Measurement of Frequencies and Levels of Tones[J].Bell Sys Teeh J,1970,4(9):197-228.

[7]Quinn B G.Estimating frequency by interpolation using Fourier coefficients[J].IEEE Trans-SP,1994,42(5):1 264-1 268.

[8]齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,19(1):86-92.QI Guoqing.Accuracy analysis and comparison of some FFT-based frequency estimators[J].Journal of Vibration Engineering,2006,19(1):86-92.

[9]邓振淼,刘渝,王志忠.正弦波频率估计的修正Rife算法[J].数据采集与处理,2006,21(4):473-477.DENG Zhenmiao,LIU Yu,WANG Zhizhong.Modified rife algorithm for frequency estimation of sinusoid wave[J].Journal of Data Acquisition&Processing,2006,21(4):473-477.