磁流变液保险机构延期解除保险时间模型
王卫青,陆 静,王 炅,郑彩军
(南京理工大学机械工程学院,江苏南京 210094)
0 引言
磁流变液(Magneto Rheological Fluid,简称MRF)是一种在外加磁场作用下流变特性发生急剧变化的新型智能材料,且这种转变可控、连续和可逆[1],适应温度范围广、稳定性好、无毒安全、能与多数设备兼容,使其在许多领域得到了广泛应用。
引信磁流变液保险机构是将智能材料磁流变液应用于引信的一种新型保险机构,具有勤务处理与发射安全性高、解除保险可靠性高、延期解除保险距离可调、结构简单、经济实用等优点。北京理工大学的石庚辰教授[2]与南京理工大学的王炅教授[3]对磁流变技术在引信保险机构中的应用展开了探索性研究,陆静[4]等人也相继对磁流变液保险机构设计理论进行了研究。
延期解除保险时间是引信磁流变液保险机构的一项关键性能指标,但至今为止并没有成熟的计算方法,因此,本文通过建立合理的流体动力学模型,提出了延期解除保险时间数学模型。
1 磁流变液保险机构及其工作原理
MRF延期解除保险机构如图1所示。勤务处理时,磁流变液在永磁体磁场作用下呈固态,挡住活塞,活塞限制转子的转动,从而保障了引信在勤务处理时的安全。弹丸发射时,在后坐力作用下,永磁体剪断剪切销下落,磁流变液瞬间变成流体,磁流变液在离心力和活塞推力的作用下通过泄流孔开始泄流,泄流完成后,活塞解除对转子的约束,转子转正,雷管与导爆药对正,引信解除保险。

图1 MRF延期解除保险机构原理示意图Fig.1 Schematic diagram of MRF delay arming device
该新型磁流变液保险机构优点如下:
1)勤务处理安全性高,发射安全性高,不会出现膛炸现象;
2)机构泄流的动力源是离心力,离心力在泄流期间越来越大,因此,机构一旦开始泄流,便可保证液体完全流出,即解除保险可靠性高,不会出现哑弹;
3)机构的延期解除保险距离不仅可以随着发射时的不同转速来实现自调节,还可以通过外加磁场调节磁流变液粘度大小从而实现延期解除保险距离的实时调整;
4)结构简单可靠,经济实用,有利于实现通用化、小型化。
2 延期解除保险时间模型
延期解除保险时间是磁流变液保险机构的关键性能指标,因此,延期解除保险时间的精确计算是引信磁流变液保险机构设计的技术重点之一。
2.1 磁流变液流动性分析
目前普遍应用的磁流变液主要由磁性颗粒、载体液和稳定剂3部分构成,这使得磁流变液的流动特性与普通液体的流动特性有所不同。具体表现为:无外加磁场时,磁流变液表现出牛顿流体行为;在外加磁场作用下,磁流变液表现出粘塑性流体行为[5]。本机构磁场存在时,磁流变液并不流动,去掉磁场后磁流变液才开始流动,故可将磁流变液看做牛顿流体处理。
文献[6]研究表明:当磁流变液内部铁磁颗粒体积分数小于30%且无外加磁场时,磁流变液的力学性质符合均匀介质模型,磁流变液在管道中的流动形态符合均匀介质的流动规律,这与本机构中磁流变液在液筒中的流动具有相似性,实际应用的稳定型磁流变液的铁磁颗粒体积分数一般小于35%,因此可以将流体看做均质的。
另外泄流孔的直径比铁磁颗粒的直径至少大两个数量级,因此可以忽略磁流变液经过泄流孔时,铁磁颗粒对流场的影响。
目前,磁流变液最大的不足是其长期储存后会出现悬浮颗粒沉淀的问题,不过这是指磁流变液在无磁场条件下储存,而本机构中的磁流变液是在外加磁场条件下储存。试验表明在外加磁场且液量很少的条件下,磁流变液中的铁磁颗粒几乎不会发生沉淀。因此在本问题中,可以忽略铁磁颗粒沉淀对流场的影响,把液体看做均质的。不过对于引信这种高安全性要求的产品来说,必须进一步研究磁流变液材料特性,寻找一种几乎不会发生沉淀的磁流变液。关于这方面内容,本文暂不作讨论。
2.2 流体动力学模型的建模前提及假设
根据实际问题对理论模型作如下假设:
1)忽略磁场对磁流变液流动的影响,认为磁流变液作粘性流动,泄流孔均匀泄流,把流体看做均质,采用不可压缩粘性流体定常流动模型;
2)近似认为流体粘性与温度无关,流场可独立于温度场之外求解;
3)不考虑摩擦力,在该流场中仅考虑离心力对流速的影响,弹丸角速度ω在泄流期间不变。
2.3 延期解除保险时间数学模型
本问题可以视为液压系统中的孔口出流问题,小孔出流模型如图2所示。

图2 小孔出流示意图Fig.2 Schematic diagram of small orifice discharge
小孔出流根据孔径和孔长的相对大小,可以分为薄壁小孔、短孔和细长孔。

表1 小孔的类型[7]Tab.1 Types of small orifice
根据本机构尺寸,本机构的泄流孔属于短孔,由流体力学知识可得流经小孔的流量q为:

式中,A0为小孔截面积;C d为流量系数;Δp是小孔前后压差;ρ是磁流变液的密度。C d与泄流孔径d、孔长l、雷诺数Re有关,可由文献[7]查出。
由于液筒长度很短,忽略磁流变液在液筒中流动因摩擦力造成的沿程压力损失,Δp相当于磁流变液与活塞所受的离心力产生的压强:

式中,ρ为磁流变液密度,m为活塞质量,l1为流体实际长度,l2为活塞与弹丸轴心的平均距离,l3为流体的相对质心,r1为液筒内径,ω为弹丸转速。
由式(1)与式(2)可得泄流孔流量q为:

则泄流时间t为:

式中,r0为泄流孔半径。由式(4)可以看出:在其他参数不变的情况下,可以通过调节泄流孔径r0达到快速调节泄流时间t的目的。另外,也可以调节外磁场强度的大小改变磁流变液粘度,进而改变流量系数C d,达到外磁场控制泄流时间的目的,这也体现了磁流变液用于引信延期解除保险机构的优越性。
由内弹道理论[8]得弹丸炮口初速与炮口旋转速度的关系为:

式中:v 0为炮口速度,ω0为炮口旋转速度,d为火炮口径,αg为炮口缠角。
由式(5)可以看出,弹丸炮口速度v0越大,弹丸速ω越大,机构的延期解除保险时间t越短,而机构的延期解除保险距离S=v0t。可见,该机构的延期解除保险距离不会受装药量大小的影响而有很大散布,这有利于实现机构的通用化。
2.4 算例
以某火炮内弹道参数为例,将相关数据代入式(4),可得:当泄流孔半径r0=0.4 mm时,延期解除保险距离可达到60 m;而得当泄流孔半径r 0=0.2 mm时,延期解除保险距离可达到200 m。
3 MRF保险机构延期解除保险时间流场数值仿真
Ansys程序中的FLOTRAN CFD分析功能是一个用于分析二维及三维流体流动场的先进工具,下面利用Ansys软件来进一步分析延期解除保险时间数学模型的正确性[9]。
3.1 仿真过程
1)有限元模型建立
考虑机构对称性和载荷对称性,为简化计算,取机构的 1/2模型进行分析,选FLUID142单元,对敏感区域泄流孔处进行网络加密控制,采用自由网格划分法。建立的机构有限元模型如图3所示。

图3 泄流机构有限元模型Fig.3 Finite element model of discharge device
2)施加边界条件
壁面采用无滑移固定壁面条件,对称面施加对称边界条件。进口边界相对压力取均布的7个点,出口边界取充分发展条件,相对压力为零。
3)设计分析参数
设计材料参数:磁流变液密度ρ=3.005 g/cm3粘度η=0.25 Pa◦s;
设计流体环境:角速度取某火炮炮口转速,工作温度为25℃,流域参考压力取为101 325 Pa,流动状态为稳态定常流动,只考虑连续方程和动量方程,不考虑传热方程即能量方程,其他参数采用默认值。
3.2 仿真结果及分析
仿真结果如图4—图7所示。
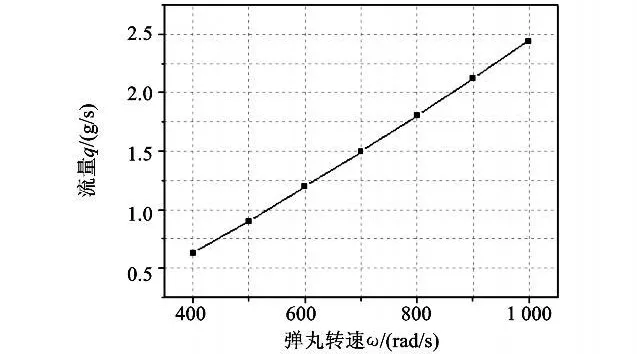
图4 弹丸转速-泄流孔流量关系曲线Fig.4 The relation curve between projectile rotating speed and mass flow

图5 泄流孔-流量关系曲线Fig.5 The relation curvebetween discharge hole and mass flow
由图4可知,弹丸转速与泄流孔流量呈线性关系,图5(b)显示,泄流孔流量与泄流孔截面积呈线性关系,这些与式(3)相符。对比图4和图5(a)可以看到,泄流孔径对流量的影响大于转速对流量的影响,即可通过改变泄流孔径快速调节泄流时间。

图6 磁流变液粘度-泄流孔流量关系曲线Fig.6 The relation curve between viscosity of magneto-rheological fluid and mass flow

图7 不同孔径时弹丸转速与流量关系曲线Fig.7 The relation curve between projectile rotating speed and mass flow considering different apertures
不同温度下,磁流变液的零磁场强度粘度一般在0.1~0.4 Pa◦s之间变化。图6表明,此区间内粘度对流量的影响较小,这也与短孔出流中,粘度对流量的影响较小相吻合,因此温度对流量的影响较小。
图4、图5、图6的仿真结果表明:仿真模拟得到的机构性能曲线的变化趋势与理论推导出的特性曲线是一致的,可见延期解除保险时间公式正确。
由图7可以看出:泄流孔径越小,弹丸转速对流量的影响越小,即小泄流孔可以减小应用时弹丸转速散布对机构延期解除保险时间的影响,机构的弹道环境适应性能提高,另一方面泄流孔径太小会影响液体的流动性。
对于本机构,根据内弹道参数施加相应的载荷和仿真环境,可得机构的泄流时间为t=0.19 s。在相同载荷下,根据式(4)计算所得的泄流时间为t=0.18 s。仿真与理论计算相对误差率仅为5.6%,可见对模型的简化是合理的,所建流场动力学模型和延期解除保险时间数学模型正确。
4 延期解除保险时间试验及结果分析
自制试验测试系统如图8所示:测试原理为机构开始解除保险(本机构表现为磁体撤离)时给测试系统一个信号,机构解除保险(本机构表现为转子转正)时再给测试系统一个信号,两个信号间隔时间即为机构的延期解除保险时间。

图8 延期解除保险时间测试系统Fig.8 Delay arming tine test system
以磁流变液为工作介质,以泄流孔孔径为试验变量,将机构安装在离心机上,在某一转速条件下,得到泄流孔径与延期解除保险时间的关系曲线如图9所示。

图9 泄流孔孔径-延期解除保险时间曲线Fig.9 The relation curve between semidiameter of discharge hole and delay arming tine
图9 显示:理论计算曲线与试验曲线吻合很好,两曲线最大相对误差小于15%。可见,机构流体动力学模型和延期解除保险时间数学模型正确。另外试验结果显示:机构的延期解除保险时间可以达到750 ms,这可以满足引信炮口安全距离要求。
5 结论
本文通过建立合理的流体动力学模型,提出了磁流变液保险机构延期解除保险时间数学模型。该数学模型反映了弹丸转速、泄流孔孔径和磁流变液粘度,与延期解除保险时间的关系。仿真与试验结果表明:1)机构流体动力学模型和延期解除保险时间数学模型误差不大于15%,这为机构延期解除保险时间的准确预测提供了理论依据,也为机构的优化设计、性能改善、通用化和小型化提供了相应的理论参考。2)延期解除保险时间对泄流孔孔径的变化比较敏感,对磁流变液因温度变化导致的粘度变化不是很敏感。通过合理设计影响泄流时间的几个因素,MRF延期解除保险机构能够满足引信炮口安全距离要求,具有一定的推广应用价值。
[1]Carlson JD.MRfluids and devices in thereal world[C]//Proc of the Ninth International Conference Electro-rheological Fluids and Magneto-rheological Suspensions.Singapore:World Scientific Publication,2005:531-538.
[2]刘子星,隋丽,石庚辰.磁流变体远解机构运动学分析.[C]//中国兵工学会第14届引信学术会议论文集.西安:中国兵工学会引信专业委员会,2005:136-139.
[3]王炅,李良军,邵旋,等.磁流变技术在引信安全系统中应用探讨[J].探测与控制学报,2006,28(6):11-13.WANG Jiong,LI Liangjun,SHAO Xuan,et al.Study on the application of magnetorheological fluids in safety and arming device of fuze[J].Journal of Detection&Control,2006,28(6):11-13.
[4]陆静,王炅,常娟.引信旋转式磁流变液保险机构研究[J].探测与控制学报,2009,31(3):14-18.LU Jing,WANG Jiong,CHANG Juan.Fuze revolving delay arming device using magneto-rheological fluid[J].Journal of Detection&Control,2009,31(3):14-18.
[5]贺建民,黄金,钟银辉.磁流变液在圆筒间的粘塑性流动[J].功能材料,2006,37(6):992-993.HE Jianmin,HUANG Jin,ZHONG Yinhui.Viscoplastic flow of the MRfluid between two cylinders[J].Journal of Functional Masterials,2006,37(6):992-993.
[6]周刚毅,金昀,张培强.磁流变液管道流模式流动行为的实验研究[J].中国科学技术大学学报,2000,30(1):46-50.ZHOU Gangyi,JIN Yun,ZHANG Peiqiang.Experimental research on the flow behavior of magnet-reological fluids in fixed magnetrode configuration[J].Journal of University of Science and Technology of China,2000,30(1):46-50.
[7]陆敏恂,李万莉.流体力学与液压传动[M].上海:同济大学出版社,2006.
[8]王靖君赫信鹏.火炮概论[M].南京:南京理工大学出版社,1991.
[9]刘华,梁川,莫政宇,等.测流孔板数值模拟及流量系数的分析[J].西南民族大学学报(自然科学版),2007,33(3):602-607.LIU Hua,liang Chuan,Mo zhengyu,et al.Numerical stimulation and analysis of discharge coefficient of orifice in conduit to measure discharge[J].Journal of Southwest University for Nationalities(Natural Science Edition),2007,33(3):602-607.

