浅谈模糊综合评判在招标采购中的应用

郝巍旭

招标投标是在市场经济条件下进行大宗货物买卖,工程项目建设的发包与承包,服务项目的采购与提供所采用的一种交易方式。近年来在企业货物采购和工程建设项目中大力推行招标投标制度,将竞争机制引入采购过程,与供求双方“一对一”的直接交易方式相比明显具有优越性。本文中是以专家评分为依据,用模糊综合评判方法对招标过程中各投标单位的被评价要素赋予权重,构造综合评价指标,对投标企业进行模糊综合评判,选出最优秀的企业作为第一中标候选单位。

1 模糊综合评判模型的建立

1.1 确定指标体系

对某一事物进行评价,若评价的指标因素为ui(i=1,2,…,m),则ui便构成一个评价因素的有限集合为:U={u1,u2,…,um}。各因素 ui(i=1,2,…,m),即代表各影响因素,这些因素都具有不同程度的模糊性。

1.2 确定指标的权重

各个因素的重要程度一般不同,因此为了反映各因素的重要程度,对各因素赋予相应的权数ai(i=1,2,…,m),由各权数组成的集合为:A={a1,a2,…,am},称为因素权重,简称权重集。

通常,各权数ai(i=1,2,…,m)应满足归一性和非负性条件:它们可以视为各因素 ui(i=1,2,…,m)对“重要”的隶属度。因此,权重集可视为各因素集上的模糊子集,表示为:

各个权数一般由人们根据实际问题的需要主观的确定,也可以按确定隶属度的方法来确定。

1.3 确定评语集

评语集也叫备择集,是对评判对象可能做出各种评判集合的总体。用字母 V表示,即 V={v1,v2,…,vm},各元素vi(i=1,2,…,n)即代表各种可能的总评判结果。

1.4 构造评价矩阵

单独对一个影响因素进行评判,以确定评判对象对备择集元素的隶属度,称为单因素模糊评判。设评判对象按因素集中第i个因素 ui进行评判,对备择集中第 j个元素vj的隶属程度为rij,则按第 i个因素ui评判结果,可以用模糊集合Ri表示。

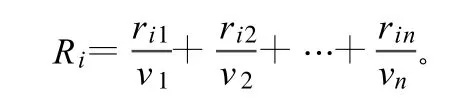
其中,Ri为单因素评判集,它是备择集 V上的一个模糊子集,可以表示为:Ri={ri1,ri2,…,rin}。由此,可得到相应的每个因素的单因素评判集。将各个因素评判集的隶属度排列成行,构成矩阵R即为评判矩阵。

1.5 进行综合评判

模糊综合评判可表示为:B=A·R。

其中,B为模糊综合评判集;bj为模糊综合评判指标,即考虑所有因素影响时,评判对象对备择集中第 j个元素的隶属度。

1.6 评判指标的处理

得到评判指标 bj(j=1,2,…,n)之后,便可根据以下几种方法确定评判对象的具体结果。

2)模糊分布法。这种方法直接把评判指标作为评判结果,或将评判指标归一化,用归一化的评判指标作为评判结果。具体做法如下:

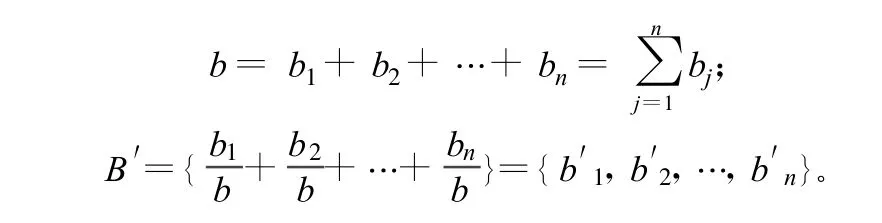
其中,B′为归一化的模糊综合评判集;bj(j=1,2,…,n)为归一化的模糊综合评判指标。这样评判的各个指标,具体反映了评判对象在被评判的特性方面的分类状态,从而可根据需要做出灵活的决策处理。

2 模糊综合评判在招标采购中的应用

2.1 确定评价指标集

U={u1,u2,u3,u4}={投标报价,技术力量,企业资质,企业信誉}。

2.2 确定权重集

在实际中,由于不同招标单位对投标者的各项能力要求程度不同,所以,不同的招标单位,对投标单位的各个能力因素赋以不同的权重,对要求高的能力因素赋以较高的权重,对要求低的能力因素赋以较低的权重[4]。本文按照通常对建设工程项目的各因素权重赋值,具体如下:A={0.3,0.4,0.2,0.1}。

2.3 确定评语集

V={满意,比较满意,不太满意,不满意}。

对各等级分别赋值,“满意”为 9分,“比较满意”为7分,“不太满意”为5分,“不满意”为3分,得赋值矩阵为:

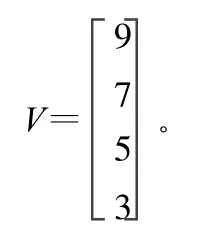
2.4 构造评价矩阵

在评标前,由招标人和专家库中抽取的专家组成评标委员会,一般人数为3人以上。本文假设评标委员会由9人组成。评标委员会对投标企业的“投标报价”评判结果是:5人为“满意”,占总人数的 60%;2人为“比较满意”,占总人数的 20%;1人为“不太满意”,占总人数的 10%;1人为“不满意”,占总人数的10%。这样,我们就可以得到“投标报价”的隶属度分别为:0.6,0.2,0.1,0.1。对A企业的各单因素评判结果如下:

Ra1={0.6,0.2,0.1,0.1},Ra2={0.5,0.3,0.1,0.1},

Ra3={0.4,0.2,0.2,0.2},Ra4={0.2,0.4,0.2,0.2}。

构造A企业的评判矩阵为:

同样可得到B,C,D三家企业的评判矩阵。

2.5 进行综合评价

Ba=A·Ra={0.48,0.26,0.13,0.13}。同样,Bb={0.42,0.27,0.16,0.15},Bc={0.43,0.28,0.16,0.13},Bd={0.33,0.31,0.20,0.16}。

2.6 评判指标的处理

1)由最大隶属度法可知,中标候选单位排序为A,C,B,D,A企业为第一中标候选单位。

2)模糊分布法。对A企业的评判结果归一化处理:0.48+0.26+0.13+0.13=1。遍除每一指标,得到归一化后的模糊综合评判集为:B′a={0.48,0.26,0.13,0.13}。

3)为了更加直观的得出被评判单位的能力程度和排序,我们用B乘以等级赋值矩阵V,即可得到各个投标企业综合评判结果的数值:

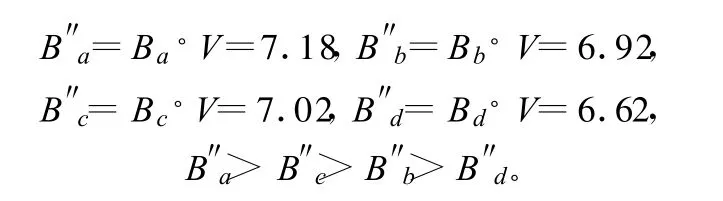
由此可以直接得到:A企业排名第一,C企业排名第二,B企业排名第三,D企业排名第四,并由评标委员会推荐A企业为第一中标候选单位。

3 结语

通过以上的分析,我们可以看出,模糊综合评判方法在招标采购中的应用比传统的评估方法更加合理和客观,得到的结果也更直观。模糊综合评判法是主观与客观的统一,它虽然没有从根本上排除主观因素的影响,但是它最大程度上限制了主观因素。因此,模糊综合评判方法是一种比较全面、比较客观的评判方法。

[1] 冯宪芬.经济法[M].西安:西安交通大学出版社,2005:172-173.

[2] 肖盛燮,王平义,吕恩琳.模糊数学在土木与水利工程中的应用[M].北京:人民交通出版社,2004:1-2.

[3] 韩立岩,汪培庄.应用模糊数学[M].北京:首都经济贸易大学出版社,1989:2-3.

[4] 周慧峰.模糊综合评判在工程项目招标中的应用[J].中国科技信息,2009(9):79-80.