基于VBA的盾构隧道中心线坐标计算的设计

陈善云

随着国内经济的高速发展,地面交通条件的恶化,为了缓解地面交通的压力,促使城市轨道交通向地下空间发展。当正在运行的轨道交通车辆由直线进入曲线时,会产生离心力。在轨道交通中,通过采用外轨超高来平衡离心力的影响。由于轨道超高,使得列车中心产生偏移,为了保证列车在曲线盾构区间行驶时满足限界要求,在实际的盾构推进中,盾构推进中心线并不与线路中心线重合,而是按照列车中心偏移的中心线推进。轨道交通盾构区间设计中,偏移后的坐标手工计算工作量相当大,而且也无法拟合盾构推进过程中实际的缓和曲线方程。本文采用VBA和Excel编程,应用程序来代替人工计算,可大大地减轻工作量。

1 线路模型

1.1 平曲线模型

平曲线的作用是改变线路的平面走向。根据曲线类型可分为直线段、圆曲线段和缓和曲线段三种。为叙述方便,规定当沿着行进路线向右偏转时,转折角 α为正;向左偏转时,转折角α为负。

1.1.1 直线模型

如图1所示,当线路为直线时,假定已知线段起点为 A(XA,YA),线路方位角α,A点到P点的里程为l,那么P点的坐标为:

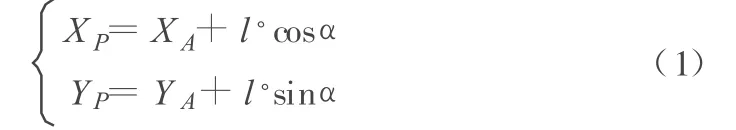
1.1.2 圆曲线模型

如图2所示,已知ZY,JD,YZ三点的坐标,圆半径 R,超距 e。施工曲线的圆曲段半径为:R′=R-e,计算出ZY到JD的方位角为α1,计算出 YZ到JD的方位角为α2,则转折角α为:α=α2-α1。

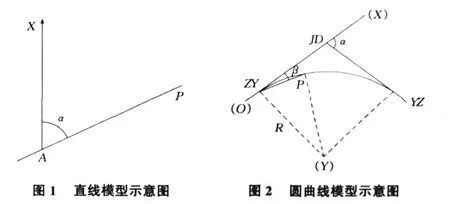
建立一左手坐标系:原点O点为缓和曲线的起点(即将直缓点作为坐标系的原点),X轴与原直线段的方向一致,Y轴指向圆心。假设圆曲线长为l0;P点在圆曲线上运动,P点到O点弧长为l,它与O点曲率半径夹角为β;P点到O点弦长为L,则:

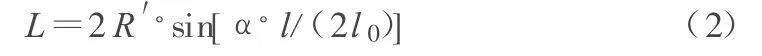
直线OP在自定义坐标中的方位角β为:

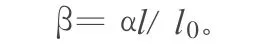
P点在自定义坐标系中的坐标为:

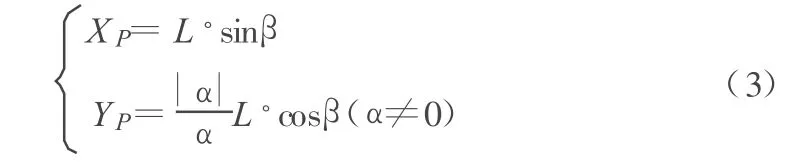
然后,将自定义的平面坐标转换为工程坐标系的坐标:

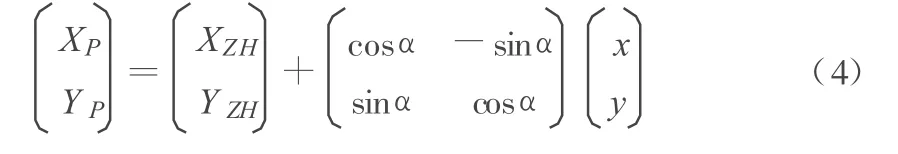
1.1.3 缓和曲线模型

如图3所示,已知ZH,HY,JD,YH,HZ五点坐标,缓和曲线长 l0(以对称曲线为例),圆曲段 R,超距 e,施工曲线的圆曲段半径为:R′=R-e;计算出ZY到JD的方位角为α1,YZ到JD的方位角为 α2,则转折角 α为:α=α2-α1。

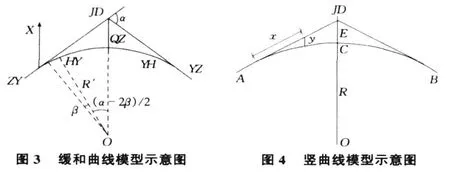
根据曲率半径的定义有:ρ=dl/dβ。

结合缓和曲线的方程式ρ=Rl0/l(R为圆曲线半径;l0为曲线长;l为所在点距起点的线路长度)有:Rl0dβ=ldl。

两端积分后再整理,可得到:β=l/(2Rl0)。

由积分三角形有:

将sinβ及cosβ用幂级数展开可得:

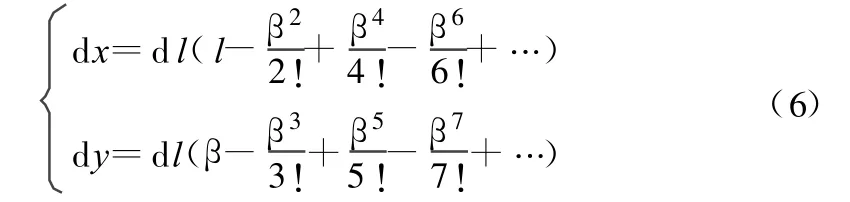
积分后略去高次项把式(5)代入式(6)并化简得:

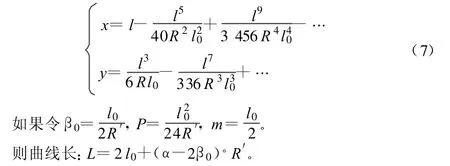
如果P位于缓和曲线上,并且至ZH点的曲线长为l,那么计算其切线支距法坐标需要分情况讨论:

1)当 0＜l≤L-l0时,以ZH 点为原点O,以 ZH点至JD 点的方向为x轴正向建立左手坐标系xoy,则:

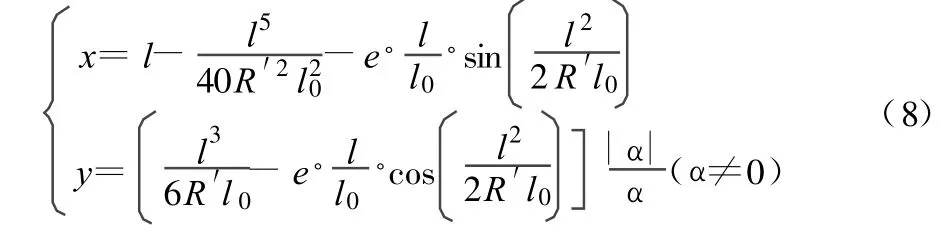
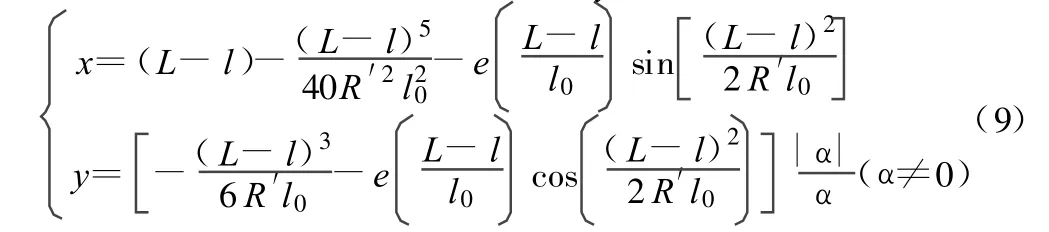
2)当 L-l0＜l≤L时,以ZH点为原点O,以ZH点至JD点的方向为x轴正向建立左手坐标系xoy,则:3)当 l0＜l≤L-l0时,以 HZ点为原点O,以 HZ点至JD 点的方向为x轴正向建立左手坐标系xoy,则:然后,将自定义的平面坐标转换为工程坐标系的坐标。由情况1)和2)转化为:

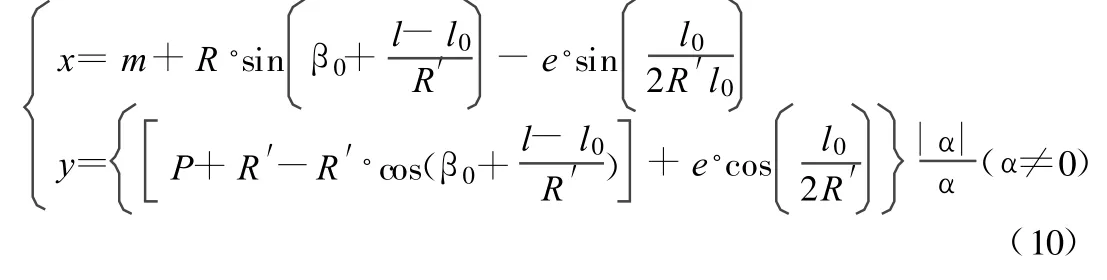
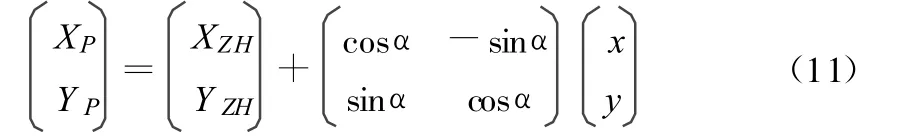
由情况3)转化为:

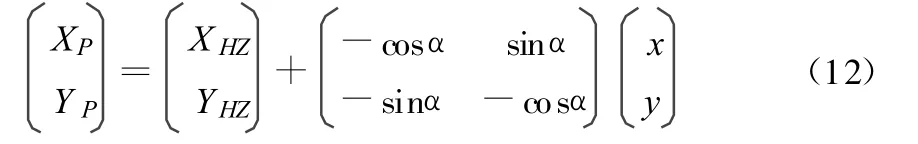
1.2 竖曲线模型

竖曲线分为以下三种:直线段、凸曲线段和凹曲线段。变坡点在曲线之上的为凸曲线,变坡点在曲线之下的为凹曲线。竖曲线的形式可以是圆曲线也可以是抛物线,我国普遍采用圆曲线形竖曲线。为叙述方便,规定当沿着行进路线高度增加时,坡度 i为正;高度减小时,坡度 i为负。

1.2.1 直线模型

假设起点A的高程为HA,线路坡度为i,那么与起点A相距里程为l的一点P的高程HP可用下式计算:

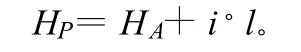
1.2.2 曲线模型

如图4所示,已知一竖曲线变坡点 JD,起点 A及其高程HA,曲中点C,线段A点到JD的坡度i1,线段JD点到B点的坡度i2,竖曲线半径 R,切线长 T,E为外矢距,那么:E=T2/2R。设离开 A点的里程x点P。令α=i2-i1,当 α＞0即 i2＞i1时,竖曲线为凹曲线,反之为凸曲线。P点高程计算为:

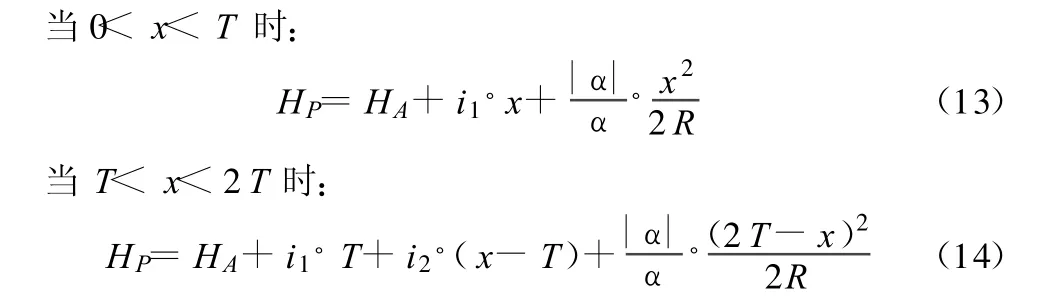
2 程序设计

2.1 主要问题分析及处理

Excel是数值数据处理应用软件,内置约300个函数。但是测量数据的独特性,Excel不能满足计算需要。如:角度的度分秒、度与弧度之间的转换和运算;方位角的范围判断及计算;曲线要素和里程的关系等。在Excel工作簿中打开菜单“工具”→“宏”→“Visual Basic编辑器”。在Visual Basic编辑器中打开菜单“插入”→“过程”,打开添加对话框,在类型选择框中选择“函数”,在范围选择框中选择“公用”,单击“确定”。此时在Excel工作簿中打开菜单。“插入”→“函数”,在函数类型中选择“用户定义”,就会发现已定义的函数已经存在,但此时它还不能执行用户的任何操作,还应在Visual Basic编辑器代码窗口添加代码。再分别定义自定义函数度分秒转换度函数DMStoD(),度转换度分秒函数DtoDMS(),方位角计算函数FWJ()等,自定义函数的函数名不能和Excel中已有函数和关键字同名。

2.2 实例应用

在杭州地铁1号线22号盾构中心坐标计算中,利用本程序计算,与设计院交付的特殊点和整百里程点三维坐标对比,最大偏差为0.5 mm,完全可以满足施工的需要。减轻了测量内业工作的强度,也很好地避免了人工计算错误而带来的重复计算。加快了内业工作速度。有效地减轻了复核的工作量,提高了工作效率和准确率。

[1]GB 50308-2008,地下铁道、轻轨交通工程测量规范[S].

[2]同济大学应用数学系.高等数学[M].北京:高等教育出版社,2003.

[3]李青岳,陈永奇.工程测量学[M].北京:测绘出版社,2008.