邓肯—张模型改进方法综述
程丽红 侯龙清 刘国林
到目前为止,国内外学者提出的土体本构模型不计其数,但是,真正广泛应用于工程实践中的模型却为数不多,邓肯—张模型为其中之一。但是,该模型也具有许多固有的、不可逾越的缺陷。针对一些不足,国内外工程界进行了广泛深入的研究,对邓肯—张模型进行了修正和改进。
1 模型的改进
1.1 为了在一定程度上反映高固结压力的影响
土体在高围压下的变形性状与低围压情况下有所不同,土体强度包线不呈直线,而是呈向下微弯的曲线[1]。这表明有效强度指标内摩擦角 φ随围压σ3的增加而降低了。为了反映这种变化,可以用折线来代替曲线,也就是在不同的压力范围用不同的强度指标。围压低于σA用φ1,围压高于σA用φ2。另一种方法是将内摩擦角 φ表示成固结压力σ3的某种函数,常用式(1),即:

1.2 考虑中主应力σ2对强度与变形的影响
1)Skermer指出将原邓肯—张模型中的侧限压力σ3用(σ2+σ3)/2来代替,偏应力 σ1-σ3用 σ1-(σ2+σ3)/2来代替,摩尔—库仑(Mohr-Coulomb)准则不变。该方法[2]在下文简称为修正A。
2)作为三维计算中的一种近似模拟方法,用球应力p、广义剪应力 q分别代替二维计算模型中相应于 σ3和σ1-σ3的位置,保持摩尔—库仑准则不变,其中应力水平和切线模量的表达式为:
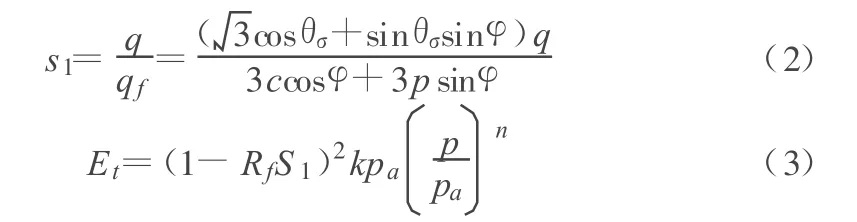
其中,θσ为应力洛德角;c为粘聚力;φ为内摩擦角;pa为大气压。该方法[3]在下文简称为修正B。
3)将 Duncan-Chang模型中凡是出现σ3为变量的地方,一律用来代替,这时摩尔—库仑强度条件为:
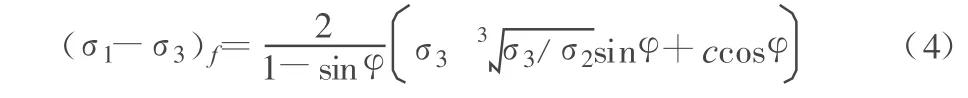
该方法[4]在下文简称为修正C。
4)由于工程中常见的变形条件是平面应变,而常规三轴试验的应变条件是轴对称的;因此,根据两种应力比可得到两种条件下摩擦角之间的关系为:
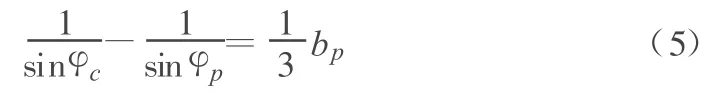
其中,φc为轴对称应力条件下的摩擦角;φp为平面应变条件下的摩擦角,由平面应变仪试验而得;bp为二者的相关系统。按照Bishop的试验研究,bp由式(6)决定:

将bp代入式(5)后可得:

由常规三轴试验求出φc后,代入式(7)即可求得平面应变条件下的 φp,再将 φp代入 Duncan-Chang模型中代替 φ,就相当于考虑了中主应力σ2对强度与变形的影响。该方法[5]在下文简称为修正D。
上述A,B,C,D四种修正方法的比较:修正A与修正B属于修正弹性模量、泊松比一类,修正D属于修正摩尔—库仑准则一类,而修正C则综合修正了弹性模量、泊松比和摩尔—库仑准则。这四种修正方法均在不同程度上反映了中主应力的影响。其中,修正A和修正C的修正效果更明显。
1.3 考虑土体结构性的修正
王立忠等在Duncan-Chang模型的基础上,考虑了土的结构的损伤,引入损伤比的概念,对Duncan-Chang模型进行了修正[7]。
对于常规三轴试验,当固结压力小于土的结构屈服应力σyp时,由试验得出的应变软化型 ε1/(σ1-σ3)—ε1关系曲线将天然结构土的变形过程分为3个阶段,这3个阶段的曲线可以分别用3段直线拟合。
对于工程中普遍关心的第 1阶段和第2阶段,将Duncan-Chang模型改用式(8)表示:
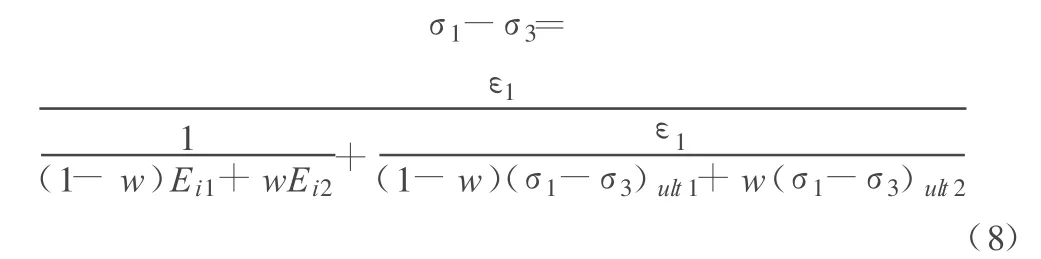
第3阶段则由于已近于重塑土,可仍然引用Duncan-Chang模型,表示为:
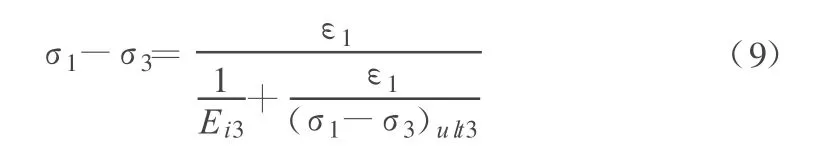
其中,Ei1,Ei2,Ei3分别为第1,2,3阶段的初始切线模量;(σ1-σ3)ult1,(σ1-σ3)ult2,(σ1-σ3)ult3分别为第 1,2,3阶段的主应力差渐近值;w为损伤比,即损伤土在总土体中所占的比重。
1993年,沈珠江建议损伤比 w按式(10)计算[10]:

而当固结压力大于土体的屈服应力σyp时,由试验得出应变硬化型曲线,对于这一类的应力—应变关系曲线,可以把其应力—应变关系看成由两个阶段组成(即第1阶段和第2阶段),不存在第3阶段,因此只需引用式(8)即可。当土体未发生损伤时,损伤比 w=0,此时式(8)形式与Duncan-Chang模型相同;而当土体结构完全破损时,损伤比 w=1,此时仍与Duncan-Chang模型相同。
1.4 考虑时间效应的E—v模型
该模型假定c,φ不随时间变化,K,n,Rf,G,F,D均与时间有关。其中,切线弹性模量和切线泊松比与时间的关系式如下:
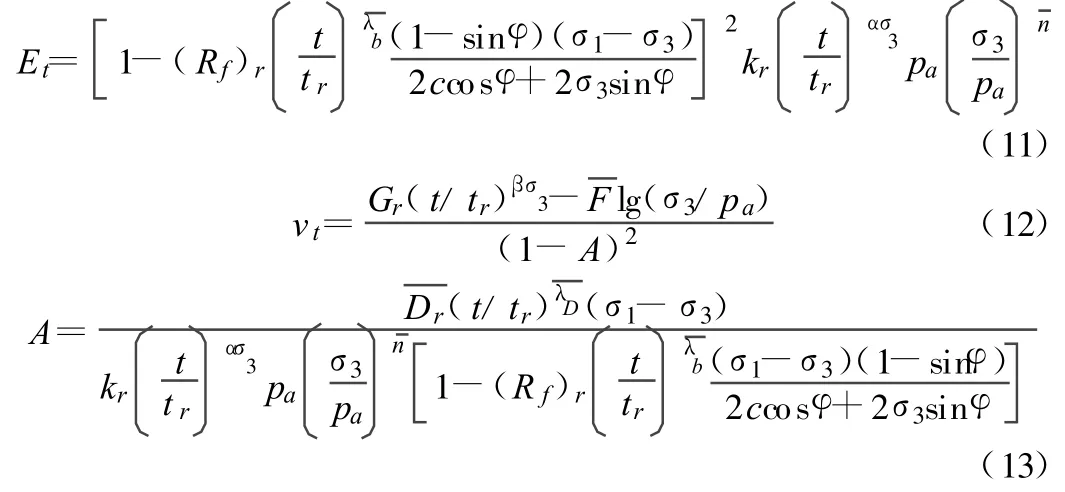
其中,tr为参考时间;α,,kr均为试验常数;(Rf)r为tr时刻的破坏比;Gr为tr时刻的G为tr时刻的D 的平均值,均为材料常数。
与时间有关的Duncan-Chang的 E—v模型不适用于蠕变急剧破坏阶段,仍然没有考虑土体剪胀等因素及超固结度的影响。
1.5 剪胀性与应变软化的考虑
为了克服Duncan-Chang模型没有考虑岩土材料的剪胀性与应变软化的特性,沈珠江提出了将剪胀引起的体应变按初应变处理,将双曲线(σ1-σ3)—ε1曲线改为有驼峰的应变软化型曲线,提出了 Mt—Et—ρ三参数的非线性模式[12]。
按初应变法考虑剪胀性[13],将{Δσ}=[D]t{Δε}改写为:
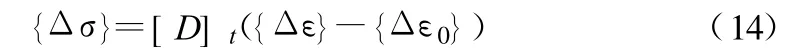
定义ρ为剪胀系数,则:
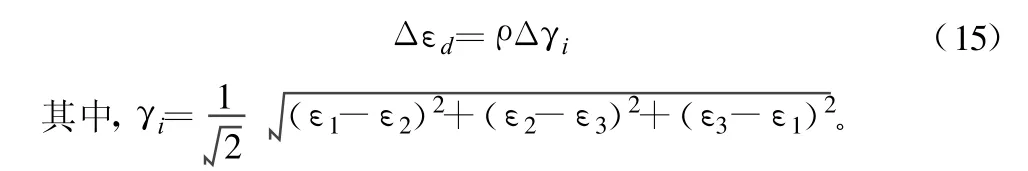
考虑试验中常用的轴对称应力条件,把式(14)简化为:
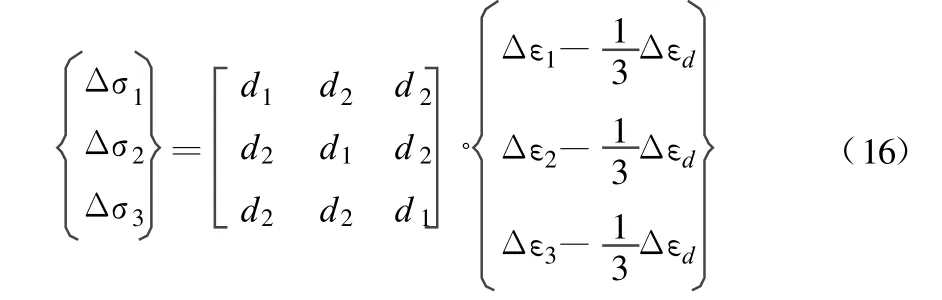
其中,

其中,Mt为切线压缩模量;Et为切线杨氏模量;vt为切线压缩比;ρ为剪胀系数。
如果通过室内试验(常规压缩试验和常规三轴试验)测定了参数 Mt,Et和vt,就可以利用式(14)进行应力应变计算。
2 结语
近几年,国内外对邓肯—张模型的研究和应用使它在不同的侧面得到一定程度的完善,具有更广泛的实用性。但任何模型都不可能面面俱到地反映土体的性质,针对土体某些方面的特点对模型进行研究的应用才是切实可行的方法。今后在模型的中主应力影响、应力路径影响、考虑土体结构性、应变软化性、剪胀性、考虑时间效应等的研究和改进中,应注重实际应用的验证和经验的积累。
[1]钱家欢,殷宗泽.土工原理与计算[M].第2版.北京:中国水利电力出版社,1996.
[2]屈智炯.土的塑性力学[M].成都:成都科技大学出版社,1987.
[3]卢廷浩,邵松桂.天生桥一级水电站面板堆石坝三维非线性有限元分析[J].红水河,1996,15(4):20-23.
[4]张学言.岩土塑性力学[M].北京:人民交通出版社,1993.
[5]谢晓华,沈珠江.土石坝计算中非线形模型的改进[J].水利水运科学研究,1998(3):43-45.
[6]孔德志,朱俊高.邓肯—张模型几种改进方法的比较[J].岩土力学,2004,25(6):971-974.
[7]王立忠,赵志远,李玲玲.考虑土体结构性的修正邓肯—张模型[J].水利学报,2004(1):83-89.
[8]沈珠江.结构性粘土的堆砌体模型[J].岩土力学,2000,21(1):1-4.
[9]沈珠江,章为民.损伤力学在土力学中的应用[A].第三届全国岩土力学数值分析与解析方法讨论[C].珠海:中国力学学会岩土力学专业委员会,1988.
[10]沈珠江.结构性粘土的弹塑性损伤力学模型[J].岩土工程学报,1993,15(3):21-28.
[11]王 琛,彭 越,刘浩吾.考虑时间效应的E—μ模型[J].岩土力学,2004,25(4):595-600.
[12]沈珠江.考虑剪胀性的土和石料的非线性应力应变模式[J].水利水运科学研究,1986(4):1-14.
[13]沈珠江.油罐地基固结变形的非线性分析[J].水利水运科技情报,1977(1):13-14.

