节理岩体变形分析与计算模型探讨

武 军

1 岩体简化模型

工程岩体是被不连续面切割的天然地质体。工程岩体的计算模式可以被归纳为四种。当不连续面的影响很小时,岩体宏观上表现为均质、各向同(异)性特征,可以采用连续介质力学模型。当岩体被一条或多条主要不连续面切割,可能产生分离与滑移等非线性效应时,宏观上仍可按均质、各向同(异)性处理,并需考虑主要不连续面的影响。当岩体中存在大量致密且呈规律/随机分布的不连续面时,岩体位移场是准连续的,可以采用“等效”连续介质力学模型。若岩体被多组不连续面切割,形成一个由有限岩块组成的区域时,各个岩块可能因转动、平移,或沿不连续面的分离、滑移等产生不连续位移场。通常,采用不连续介质力学模型。然而,岩体中广泛分布的宏观裂隙(节理)使岩体成为一种具有显著各向异性的非连续介质。对于现实岩体的分析就不能简单的采用连续介质的模型来求解,而是采用不连续介质的力学模型。

2 节理岩体的本构模型

根据多数研究者的见解,均质岩体中的节理可看作圆盘状破裂面。设其半径为a,法线方向余弦为{ni}。节面上法应力为σ(以拉为正),则该面上剩余应力为:

其中,t,f分别为该面上的剪应力和摩擦系数。

借助于断裂力学能量释放理论,由单个节理引起的变形能为:

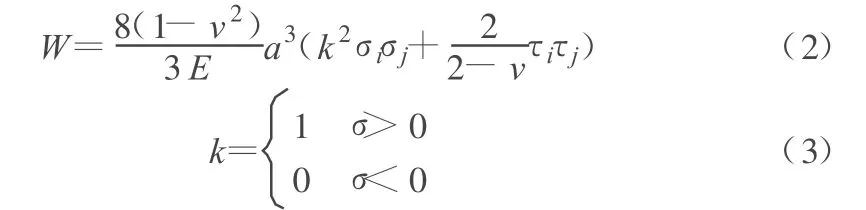
对于存在m组节理,其中心点在空间完全随机分布的情形,考虑到能量密度为广延量,由节理网络引起的应变能密度为各单个节理引起的应变能密度之和,即:

其中,λ为p组节理的体密度。

根据能量原理,由完整岩块及节理系统引起的应变能密度we和wc与等效介质的总应变能密度w有如下关系:

则由式(5)可导得节理岩体本构关系为:

其中,Cv,Cs分别为完整岩块的柔度张量及节理网络引起的柔度张量增量,且有:

其中,h=τ/t。

3 非连续变形数值分析方法

3.1 离散单元法

离散单元法是由Cundall于20世纪70年代提出的。离散单元法是针对节理岩体提出的一种适用于模拟岩土体大位移的数值方法。它是在块体准刚性假设的前提下,以牛顿第二定律为理论基础建立起来的,以微小运动状态的求解模拟岩体的大位移。当所研究的块体在力系作用下或边界条件发生变化时,单元就在牛顿第二运动定律下发生平移或转动,允许调整各个块体单元的接触关系,接触关系的调整产生新的接触力,在该力的作用下产生新的位移。如此循环,在不平衡力作用下,块体产生运动。

3.2 DDA方法

DDA(不连续变形分析)是由石根华博士提出的一种新型数值分析方法。它以自然存在的节理面和断层切割岩体形成不同的块体单元,以各块体的位移作为未知量,通过块体间的接触和几何约束形成一个块体系统。在块体运动的过程中,严格满足块体间不侵入。将边界条件和接触条件等一同施加到总体平衡方程,总体平衡方程由最小势能原理求得。

3.3 拉格朗日元法

拉格朗日元法(Fast Lagragian Analysis of Contin-na,缩写为FLAC)是由Cundall加盟的ITASCA咨询集团于1986年提出的。该方法起初应用于流体力学研究每个流体质点随时间而变化的情况,即着眼于某一流体质点,研究它在任意一段时间内轨迹、所具有的速度、压力等。后来该法被移植到固体力学中,将所研究的区域划分成网格,网格的节点相当于流体的质点,然后按时步研究网格节点的运动。这种方法适合于求解非线性的大变形问题,其按时步采用动力松弛的方法求解,不需要形成刚度矩阵,不用求解大型联立方程,可用计算机解决较大的工程问题。

3.4 块体单元法

块体单元法是由任青文等改进的。该方法是在刚体弹簧元的基础上进一步改进的,以形心处的刚体位移作为基本未知量,并根据它们在外力作用下的平衡条件、变形协调条件及夹层材料的本构关系,建立起块体单元法的支配方程。同时,在块体单元间设缝单元,在由虚功原理求出各块体形心处的刚体位移后,由缝单元两侧块体的相对位移确定缝面的变形与应力。块体单元法主要适用于具有地质结构面的岩体。

4 非连续变形计算模型基本原理

4.1 广义有限单元

广义有限单元是由数学覆盖、有限物理覆盖和本构模型三要素构成。广义有限单元的数学覆盖是指广义有限单元的插值逼近空间,它是该单元广义结点的数学覆盖的重叠区域,其覆盖函数是广义有限单元的插值逼近函数。广义有限单元的物理覆盖是其数学覆盖作用的有效物理区域,是广义有限单元的积分区域,其最大区域不超越广义有限单元的数学覆盖,因此广义有限单元的物理覆盖可以是不规则区域,可在其物理覆盖外部构造其数学覆盖,进行插值,使广义有限单元能够处理复杂的物理边界。广义有限单元的本构模型是指其应力与应变的关系。可见由于数学覆盖和本构关系的不同,将构成不同特性的广义有限单元。任意广义有限单元的数学覆盖函数(即位移插值函数)可表示为:

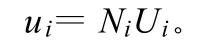
其中,Ni为广义有限单元i的数学覆盖的形函数;Ui为广义有限单元i的数学覆盖的广义自由度。

4.2 点接触力元

点接触力元是指在接触面上接触力受到力学上屈服准则和运动学上流动准则的约束。点接触力元是由接触对组成,接触对是由一个单元的角点与其相对应的另一个单元的角点或边构成,于是接触对有两种类型:角与角和角与边。广义有限单元 i与广义有限单元j间接触面ij上的界面力一般可表达为:

其中,Tij为接触面ij上的界面力的插值函数;Rij为接触面ij上的接触应力广义自由度;Tijk为接触对k在接触面ij上的接触力插值函数,R为接触对k在接触面ij上的接触ijk力,即[σijk,τijks]T;ncij为接触面ij上的接触对数。

4.3 非连续变形计算力学模型的控制方程

在多体系统实际物理剖分的基础上,用点、线和面将多体系统进行数学剖分而形成 ni个子区之和,在每个子区上可根据实际需要构造广义有限单元,令其广义有限单元数为 nei,各广义有限单元求解函数的模式可以互不相同,可能由于广义有限单元间求解函数的不连续而在广义有限单元间形成新的不连续面(接触面),可以把它当作接触面处理。令任意广义有限单元的物理覆盖为 Aij,则有和分别为位移边界、应力边界、接触边界和连续边界。

非连续变形计算力学模型的分区参变量最小势能原理可表述为:在非连续变形力学系统的当前构形和给定的外力增量作用下,对于任意子区i在满足位移边界条件的所有位移场中真实的位移使系统总势能增量泛函 ∏1i取极小值,其中接触力为不参加变分的参变量,其必须满足接触力元所受到的约束条件。

设在 t时刻非连续变形力学系统的初始应力、初始应变、初始速度和初始加速度分别为σt,εt,vt和at,在 Δt时间内,系统所受的体积力密度增量和外力增量分别为b和,系统的位移增量、速度增量、加速度增量、应力增量和应变增量分别为u,v,a,σ和ε。任意子区 i的总势能增量泛函 ∏1i为:

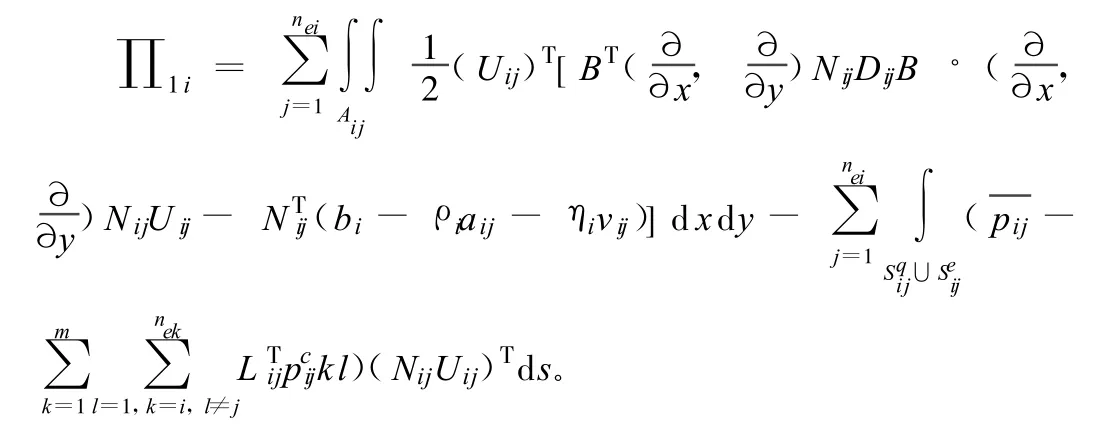
其中,第一项为子区i的总弹性势能增量;第二项为外力和摩擦力势能增量,并利用时域上的New mark逐步积分法:

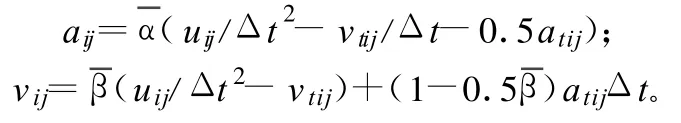
由变分驻值条件可得到:

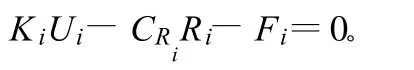
通过区分参变量最小势能原理,加上参变量的控制条件,可以得到如下非连续变形计算力学模型的整体控制方程:

5 结语

本文所提及的非连续变形计算力学模型能够比较精确地预测刚性和可变形岩质块体系统的变形和接触力,可根据变形的变化模式来判断系统是否达到极限平衡状态,从而可得到系统处于极限平衡状态所受到的极限荷载或临界抗剪强度及其相应的变形状态和接触力分布,进而可得到安全系数。系统的控制方程可以适用于复杂的边值问题。初步研究表明这种非连续变形计算力学模型可以作为极限平衡分析的一种有效的数值分析方法,在岩土边坡稳定分析中将具有广阔的应用前景。

[1]唐春安,王述红,傅宇方.岩石破裂过程数值试验[M].北京:科学出版社,2003:41-47.

[2]朱浮声,杜 轩,万明富.非均质性对岩体应力场反分析结果的影响[J].东北大学学报,2005,26(10):34-35.

[3]伍法权.节理岩体的本构模型与强度理论[M].北京:中国科学院地质研究所,2006.

[4]栾茂田,黎 勇,杨 庆.非连续变形计算力学模型在岩体边坡稳定性分析中的应用[J].岩石力学与工程学报,2000,19(3):23-26.

[5]任青文.块体单元法及其在岩土稳定性分析中的应用[J].河海大学学报,1995(2):1-3.