建立时空图 教学相对论

冯德强 黄 雄

(南菁高级中学·新校区 江苏 江阴 214400)

时空图以直观清晰的几何图象,用来理解、解释和讨论狭义相对论所依据的原理以及运动学效应,有利于学生建立崭新的时空观,使自然界的基本物理图景得到更新和不断完善.

1 惯性参考系、事件及运动的图示法

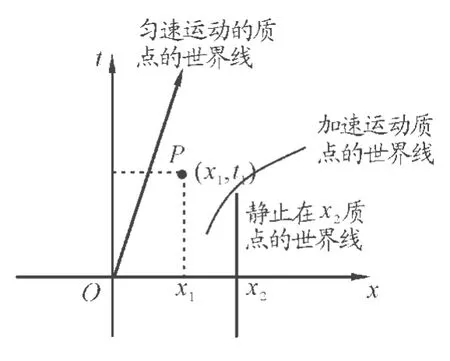
图1

在惯性系中发生的一切物理事件,都可以用固定在此惯性系的坐标系及时钟描写,这本来是一个四维的时间-空间问题.为简单起见,本文用二维时空图来讨论问题,即空间坐标x和时间坐标t组成的时空图,如图1所示.一个事件就用此图上一个点表示,如图上P点,它的坐标就表示此事件的位置及时间.在时空图上随时间变化的质点的运动轨迹一般是一条曲线,这个轨迹实际上是质点随时间在空间位置上变化的“历史”,也称为这个质点的世界线.匀速运动质点的世界线是一条直线,加速运动质点的世界线是一条曲线,静止在某一时空参考系的质点x2的世界线是平行于时间轴的直线.

2 两个相互做匀速直线运动的惯性系的时空图

如图2所示,静止参考系S和运动参考系S′,S′和S 在 t=0,t′=0时,原点 O 、O′重合,运动系S′的x′轴与静止系S的x轴方向相同,且沿x轴的正方向以速度v运动(人教2007版《选修3-4》第99页图15.1-1).狭义相对论下的时空图,时间和空间采用相同的单位,所以用ct代替t作时间轴.零时刻从坐标原点发出的光信号的世界线为x轴和ct轴之间夹角的角分线.过时空原点且与 ct轴的夹角为θ的直线,表示质点O′向x正方向以速度v匀速运动,这条世界线就是相对S以速度v匀速运动的S′系的时间轴ct′.与ct′相对应的空间轴x′和x轴的夹角也应为θ,这样光信号的世界线在两个参考系中角分线的地位不变,这正是光速不变原理所要求的.顺便指出,在给出的时空图上,两个参考系一个在形式上时空坐标之间为90°;另一个在形式上时空坐标之间为非90°的,但两个坐标系仍然都是正交坐标系,尽管在给出的一个图上其中一个坐标系视觉上是“倾斜”的.

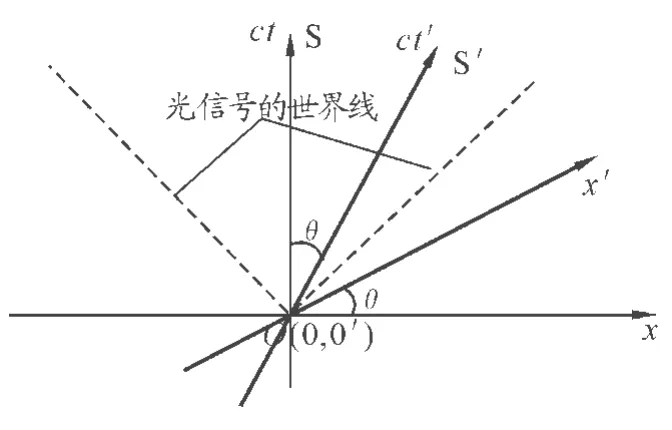
图2

3 “同时”的相对性

见人教2007版《选修3-4》第101页图15.2-1及文字情境,应用时空图辅助教学.

3.1 建立时空图

设地面为S系,匀速行驶的列车为S′系;两个参考系的空间原点O、O′(车厢中央)在t=t′=0重合时 ,车厢前壁 、后壁的位置分别在 A 、B;O′、A 、B 在S′系中是静止的,它们的静止线如图3所示.

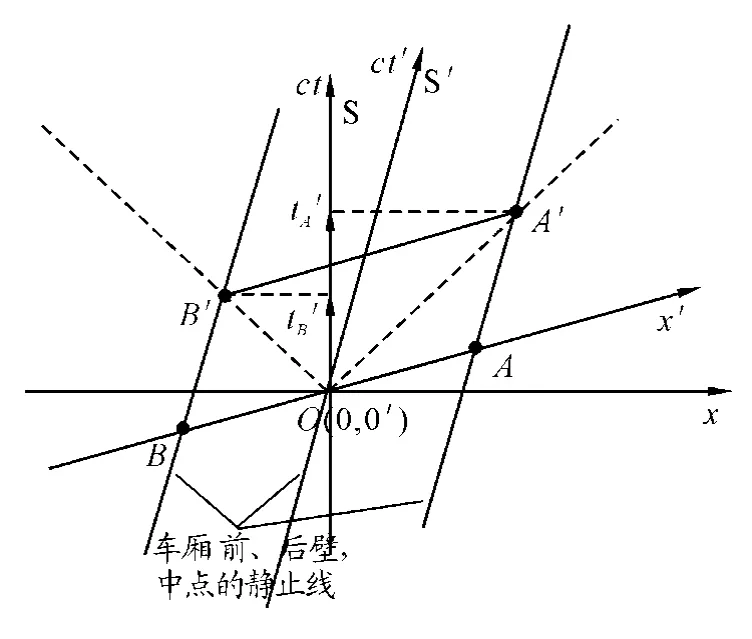
图3

3.2 事件、世界线

车厢中央的光源发出的一个闪光传播,在S′系来看,车厢前壁A、后壁B的世界线即为平行于ct′轴的静止线,它与光信号世界线交于 A′、B′.由几何关系可知 ,A′B′∥AB ∥x′轴 ,即 A′、B′在同一等时线上;在S系来看 ,A′、B′不在同一等时线上,且tA′>tB′,所以光到达前壁A的时刻也就晚些.(图上的表示,已约定 c=1,说明见后)

4 时间和空间的相对性

见人教2007版《选修3-4》第103页图15.2-4及文字情境,应用时空图辅助教学.

高速列车车厢安装着一个墨水罐,它每隔一定时间滴出一滴墨水.当t=t′=0时,墨水罐P′,滴出第一滴墨水落在地面P点,令 xP=x′P;在t′时刻,第二滴墨水落在地面Q点,S系中空间坐标为xQ,这时在地面Q点时钟指示的时间为t(地面上各地的钟都经过校准),如图4所示.车上的人测得,墨水在地面上形成P、Q两个墨点的时间间隔为t′,地面上的人测得的时间间隔为 t.

图4

由于“同时”的相对性,两个相互运动的参考系已经没有相同的等时线了,应该如何确定t和t′的关系呢?

用狭义相对论原理和光速不变原理来解决这个问题.设想S系位于空间原点O的观察者,在S系时刻t1向S′系位于空间原点O′的观察者发出一束光,在S′系位于O′的观察者在收到这个光信号的时刻为 t′;O′收到后立即用镜子将光线反射给S系的O,O在t2时刻收到反射回的光线.

可以证明,t1、t′、t2之间的关系应该满足

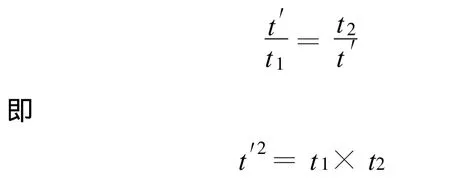
这正体现了惯性系是平权的,在时空原点重合的条件下,任意时刻,O发出光线(t1),O′收到光线(t′),和 O′发出光线(t′),O 收到光线(t2),这两种情况下,各自时钟(t和t′)测量到的时间关系的比例应该是相等的.读者可仔细研读图4,t1P′、P′t2是沿正负方向传播的光信号的世界线,所有正方向或负方向传播的光信号的世界线都是平行的.在S系来看,经时间 t,S′系的空间原点O′(即 P′)运动到Q,xQ=vt,据此确定在t1由O发出的光线在传播过程中各事件对应的时刻,如图4所示.

在S系的时刻 t,事件 P′(S′系空间原点O′在t′时所处的时空位置)与S空间原点O的距离为vt,即图上P′到t之间的连线.由于光速不变原理,则

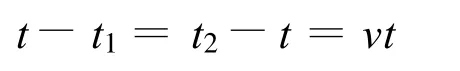
由此有

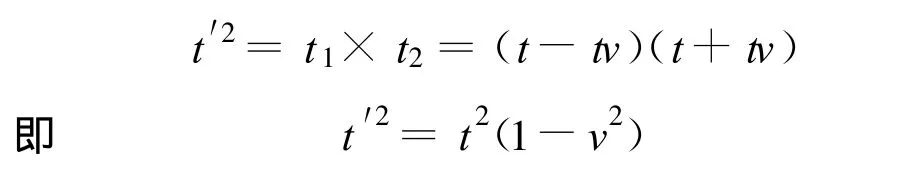
这里需说明一点,纵坐标以 ct为轴,为方便起见,约定c=1,这样v是以光速为准的相对速度值,有tanθ=v.至此我们容易得到

式中 t′表示车上观察者(相对静止)测得两滴墨水的时间间隔(即Δτ),t表示车下观察者测得两滴墨水的时间间隔(即Δt),结果是不一样的.显然此式与课本第103页的(2)式是等价的.

由于时空图的对称性,空间轴上事件的坐标变换与时间轴上的坐标变换有相同的形式,所以对于地面上PQ之间的距离,在S、S′系来测量分别是xQ、xQ′,结果也是不一样的,两者的关系是式中xQ′表示车上观察者测得地面上两滴墨水之间的空间距离,xQ表示车下观察者(相对静止)测得地面上两滴墨水之间的空间距离.这与课本第102页的(1)式是等价的,不过这里PQ相当的“尺”是放在地面上的,课本第102页图15.2-3中,尺是放在车上的.

5 μ子寿命的问题

μ子是一种不稳定的粒子,在静止参考系中观察,它的固有寿命Δτ=2×10-6s.宇宙线在大气上层产生的μ子速度v极大,可达v=0.998(约定c=1),如果没有钟慢效应,μ子不可能达到地面的实验室.如图5所示,S为实验室参考系,S′是固连在μ子上的参考系,t′=Δτ,由前述(1)式知

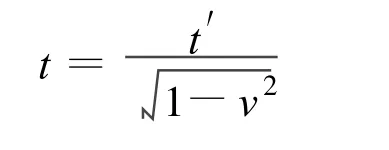
所以

这与实验室观测结果基本一致.

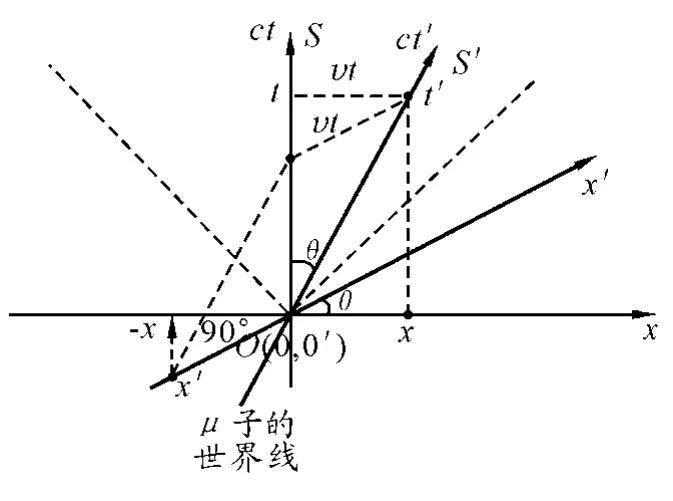
图5

再从μ子参考系测量,观察者认为μ子的寿命仍为Δτ,但是大地正向它扑面而来,μ子观测到寿终时地面相对它的运动距离

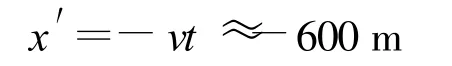
不过在实验室中测量,由前述(1)′式知

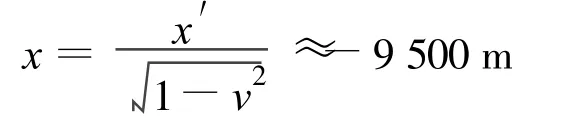
这在μ子观测者来看,实验室的尺子(运动的尺)短了,短尺自然量多了.

本文试图应用时空图辅助爱因斯坦相对论的教学,问题情境均取于课本.笔者以为相对论原理导致时空的相对性,如何把时空变得直观有形,如何把原理体现在时空图上,这是时空图辅助教学的目标.

1 赵凯华,罗蔚茵.力学.北京:高等教育出版社,1995.

2 (美)约翰·C·泰勒著.鲍永宁译.自然规律中孕育的统一性.北京:北京理工大学出版社,2004