基于混沌同步的永磁同步电机控制*

岳永恒，王茂，孙光辉

(1.哈尔滨工业大学空间控制与惯性技术研究中心,黑龙江哈尔滨150001;2.东北林业大学交通学院,黑龙江哈尔滨150040)

近年来，随着大功率电子器件的快速发展，永磁同步电机由于其高效性和良好的动态特性，在机器人、航空航天领域都得到了广泛的应用[1]。但是由于其高速和弱磁区域控制受到较高的门限电压限制[2]，大大限制了其应用。研究表明，永磁同步电机系统像很多非线性系统一样表现出多个稳态工作点，在一定条件下，可能出现极限环甚至混沌。所以研究永磁同步电机系统在稳态工作点附近的特性是近来研究的热点。大量的文献表明，永磁同步电机在动态特性上与混沌Lorenz系统具有相似性[3-5]。

混沌系统是一种确定性系统，其运动轨迹敏感地依赖于系统的初始状态，即两个相同的混沌系统从非常接近的初始状态出发，经过一定的过渡时间之后，其运动轨迹将变得完全不同。这和现实生活中的一些复杂系统所表现出来的特性非常相似，即确定性系统所表现出的随机性。系统的混沌特性在很多情况下是人们不希望的，所以针对这些系统，研究了很多的控制方法来消除混沌现象。例如混沌的自适应控制[6]、变结构控制[7]、反馈控制等[8]。此外在混沌同步方面自从Pecora和Carroll的文章(即P-C同步法)[9]发表以来，混沌同步的研究也取得了巨大的发展。

本文正是由混沌同步的观点出发，设计出永磁同步电机的状态观测器，从而构造出非线性反馈控制器，实现永磁同步电机的控制。通过简单的线性系统的零极点配置方法，便可以获得期望的运行特性,而且避免了PID校正中由于参数不当而可能出现的混沌现象。

1 数学模型

永磁同步电机的d-q模型广泛地用于控制器设计。通过Park变换很容易将电机的交流变量转换成直流变量，极大地方便了控制系统设计。永磁同步电机的d-q模型可以表示为:

其中下标q代表着q轴的变量，d代表着d轴的变量，V代表电压，I为电流，n为极对数。而相应的电磁转矩可以表示为:

更详细的内容可以参见参考文献[10]，而机电系统的动态方程表示为:

其中T(I，θ)是电机产生的转矩，Tl(t)为外部力矩。考虑到各种摩擦，Tl(t)=bω+TL，其中b为粘滞摩擦系数，TL为其他负载力矩。对于均匀气隙的电机来说，可以认为Ld=Lq。所以永磁同步电机系统可以表述为以下的模型:

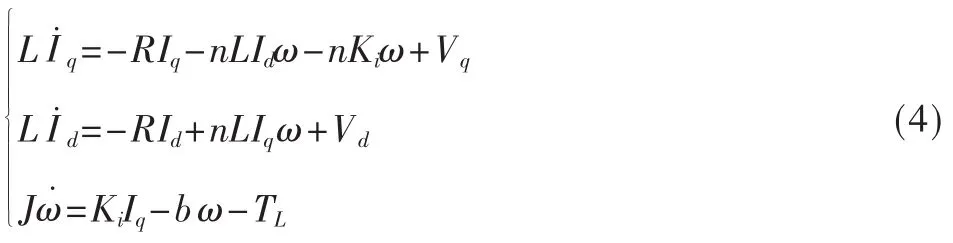
在一定条件下，上述的系统和混沌Lorenz系统具有等价的表示形式。例如采用以下的变换:

其中Σ=diag(σ1,σ2,σ3),Q=(q1,q2,q3)T,系统可以转化成著名的Lorenz系统:

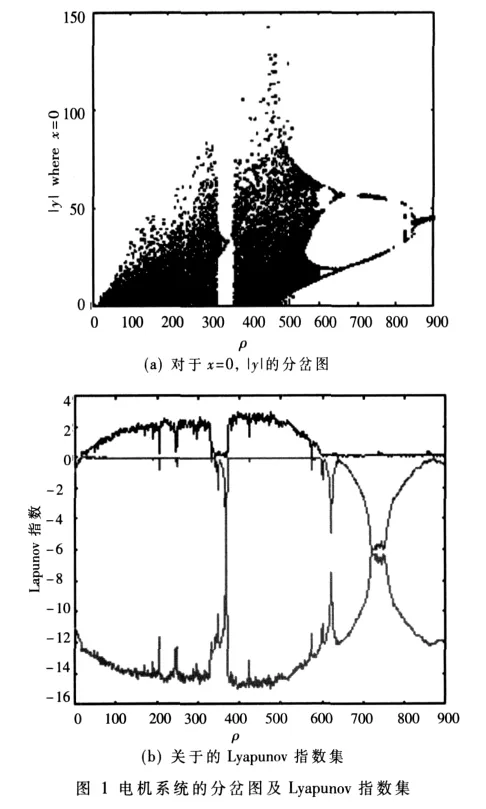
当ρ=ρH时，Hopf分岔发生；当ρ＞ρH时，系统的三个平衡点均不稳定。值得注意的是，对于给定的电机，有与之对应的δ，随之就会有确定的ρH，相对应地存在b和Vd，使得混沌现象总是能够被观察到。此外,随着b和Vd的减小，混沌现象被观察到的可能性就会越大[10]。例如，选择电机的参数为:J=5×10-6kgm2,L=0.99 mH,R=0.9 Ω,Ki=0.049,Nm/A,b=2.3×10-2N/(rad/s),则可得到δ=10.17，而相应的电机系统分岔图如图1所示。图1描述的是当参数从0到900变化时，采用Wolf方法[11]所得到的Lyapunov指数谱及相应|y|的分叉图。更多关于奇异吸引子的内容可以参见参考文献[12-14]。

2 控制器设计

线性控制器尤其比例积分(PI)控制器在永磁同步电机速度控制中通常是首选的设计方案。简单地表述为双闭环控制系统:内环为电流环，外环为速度环。这里就以比例调节器为例，说明传统的线性调节器在永磁同步电机控制应用中的弊端。记Iqr和Idr分别为q轴和d轴的指令电流，而实际中Idr=0可以很容易得到保证[4]，则采用比例调节器的d-q电压为:

将(9)式代入(6)式可以得到:

为了得到不受驱动的Lorenz系统,可以使外部转矩TL=0，以及指令电流Iqr=0。可以得到如下的模型:

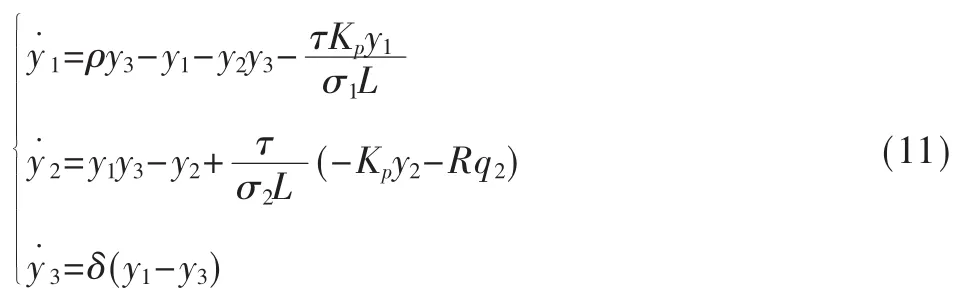
将(7)式代入(11)式，通过计算可以得到Lorenz系统族的Lyapunov指数集与反馈增益Kp的关系，如图2所示。图中计算所采用的方法同样是Wolf法，只不过此时Lyapunov指数集的计算与反馈增益Kp息息相关。

从图2可以看出永磁同步电机在较小的反馈增益Kp(Kp＜86)下能够保持稳定，随着Kp的增加，混沌化逐渐加剧。在控制系统设计时，一方面为了保证系统的响应速度，必须有较大的反馈增益；而另一方面，大的反馈增益又容易使系统混沌化。对于PI调节器，也有同样的结果。受非线性反馈的启发[14]，可以引入如下的反馈:

这里的Kqi和Kdi是为了得到期望性能而引入的反馈系数。当引入以上的非线性反馈后，系统就变成如同Y˙=AY+Kτωd的线性系统:

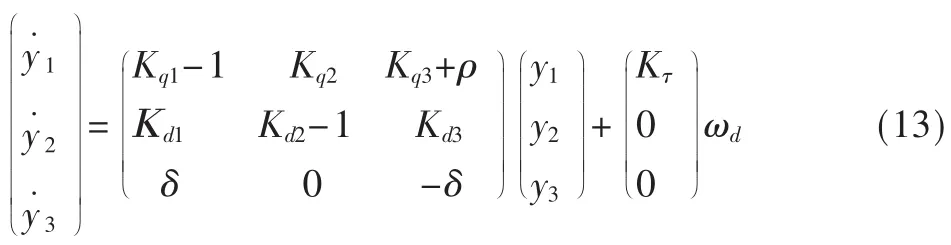
通过简单的零极点配置方法，闭环系统就能得到期望的性能。更进一步来说，实际系统中某些变量是不能直接测量的，例如现在研究的同步电机无位置传感器控制就是只能测量电机的角速度ω。为此，可以构造基于混沌同步的状态观测器，估计出其他变量，从而可以实现控制。其结构框图如图3所示。也就是说，通过构造与永磁同步电机相关的同步子系统，将控制所需的电机状态变量用通过同步后的子系统变量代替，从而形成闭环控制。

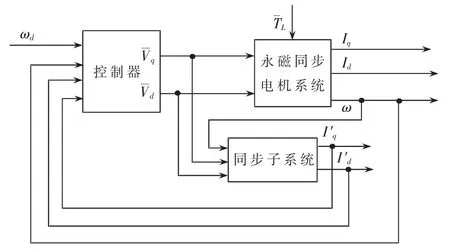
图3 基于混沌同步的非线性反馈控制方框

根据驱动-响应耦合同步原理[9],将y3(即电机角速度ω)作为驱动信号，响应系统可以写成如下的形式:

而非线性反馈则为

为了验证系统的稳定性，可以通过定义以下的误差:

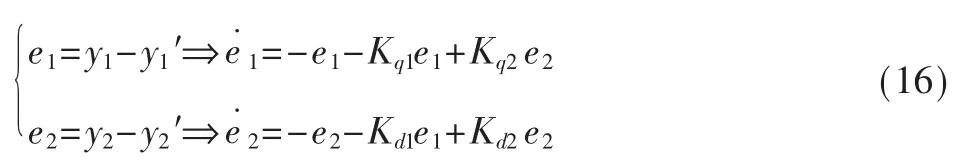
定义Lyapunov函数为V=(e12+e22)/2,则:

假定Kq2=-Kd1,Kq1＜1以及Kd2＜1，则V˙负定，系统就能稳定。事实上，可以很容易地通过零极点配置来保证系统矩阵A为负定,即保证:

从式(18)可以看出，要保证系统的稳定性，就必须保证Kq1＜1及Kd2＜1。这也就是说，只要通过零极点配置，能够保证Kq2=-Kd1，Kq1＜1及Kd2＜1，不仅能够实现永磁电机混沌系统的同步，而且能够实现基于混沌同步的观测器稳定，进而保证控制系统的有效性。例如,通过选取:Kq3=ρ,Kd3=0,Kd1=1,Kq1=Kd2=-1以及Kτ=2.7,就可以得到系统的极点为:λ1=-10.170 0，λ2=-2+i，λ3=-2-i。图4为系统的角速度ω随时间的变化过程。

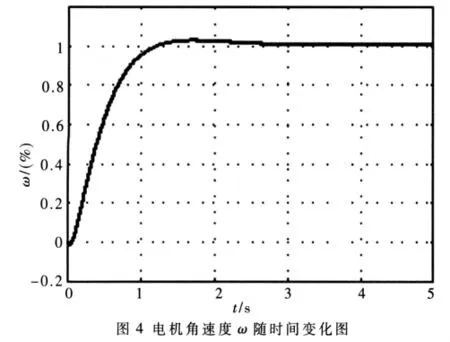
本文首先介绍了永磁同步电机与混沌Lorenz系统在数学模型上的相似之处。永磁同步电机本身是不会呈现混沌特性的，但是随着电机外部力矩的变化及q轴电压的变化，就有可能产生混沌现象。传统的PI控制器在抑制混沌上作用又不是很明显。由此引入了非线性反馈控制，该控制器能够使非线性的电机系统转化为普通的一阶系统，从而可以通过线性系统的零极点配置达到期望的响应特性。考虑到实际系统的某些变量可能无法测量，在非线性反馈的基础之上，引入了基于混沌降阶同步的状态观测器，用估计值代替某些不可测量的变量，进而构成非线性反馈，实现了电机系统的控制。同时通过Lyapunov直接法证明了观测器的稳定性。仿真结果也证明了该控制器的有效性。

[1]王立欣,王宇野,王丰欣.基于DSP的电动车用永磁同步电机的控制方法[J].电机与控制学报,2005,9(1):51-54.

[2]JAHNS T M,KLINMAN G B,NEUMANN T W.Interior permanent magnet synchronous motors for adjustable-speed drives[J].IEEE Transactions on Industrial Applications,1986,22(4):738-747.

[3]HEMATI N,KWATNY H.Bifurcation of equilibria and chaos in permanent-magnet machines[C].Proceedings of the 32nd conference on Decision and control,December 1993:425-429.

[4]杨志红,姚琼荟.无刷直流电动机系统非线性研究[J].动力学与控制学报,2006,4(1):59-62.

[5]HEMATI N.Strange attractors in brushless DC motors.IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Application.1994,41(1):40-45.

[6]LI Shuang,XU Wei,LI Rui Hong.Synchronization of two different chaotic systems with unknown parameters[J].Phys.Lett.A,2007,361(1):98-102.

[7]LI Xiao Run,ZHAO Liao Ying,ZHAO Guang Zhou.Sliding mode controlfor synchronization of chaotic systems with structure or parameters mismatching[J].Zhejiang Univ SCI,2005(6):571-576.

[8]HUANG L L,WANG M,FENG R.Parameters identification and adaptive synchronization of chaotic systems with unknown parameters[J].Phys.Lett.A,2005,342:299-304.

[9]PECORA L M,CARROLL T M.Synchronization of chaotic systems[J].Phys Rev Lett,1990,64(8):821-830.

[10]HEMATI N,LEU M C.A complete model characterization of brushless DC motors[J].IEEE Transactions on Industry Applications.1992,28(1):172-180.

[11]GE Zheng Ming,CHANG Ching Ming,CHEN Yen Sheng.Anti-control of chaos of single time scale brushless dc motors and chaos synchronization of different order systems[J].Chaos,Solitons and Fractals,2006,27:1298-1315.

[12]JING Zhu Jun,CHANG Yu,CHEN Guan Rong.Complex dynamics in a permanent-magnet synchronous motor model[J].Chaos,Solitons and Fractals,2004,22:831-848.

[13]GE Z M,CHENG J W.Chaos synchronization and parameter identification of three time scales brushless DC motor system[J].Chaos,Solitons and Fractals,2005,24:597-616.

[14]ZAHER A A.A nonlinear controller design for permanent magnet motors using a synchronization-based technique inspired from the Lorenz system[J].CHAOS,2008,18:(1).