GPS信号阻塞情况下的EKF算法改进
肖晶晶,陆明泉
(清华大学电子工程系,北京100084)
GPS卫星定位解算是根据伪距、伪距增量等测量值,计算接收机的位置P、速度V和时间T等信息的过程。目前GPS实时定位解算中最为常用的两种方法为迭代最小二乘算法(ILS)和扩展卡尔曼滤波(EKF)。为了准确计算接收机的三维位置以及时间未知数的值,解算过程需要至少4颗卫星的测量信息。但是当GPS信号出现遮挡时,接收机只能接收到3颗卫星的测量信息,解算方程就不够4个,ILS不再适用。参考文献[1]引入EKF,利用随着时间推移的多组数据进行实时定位解算,但定位精度也很难满足用户的需求。
为了解决上述问题,本文提出了一种改进的EKF算法。利用在垂直地面方向上的位置变化缓慢这一运动特性,建立了改进EKF算法的系统模型,并通过理论分析得到了滤波器参数,最后利用真实的卫星数据进行验证。需要特别指出的是,由于本文提出的改进EKF算法利用的是在垂直地面方向上的位置变化缓慢的特征,故而该算法的适用场合为车载等地面用户的定位解算,不适合在垂直地面方向上高速运动的情形。
1 定位解算的系统模型
卫星定位解算的系统模型包括状态模型和观测模型两部分。令向量yt、xt分别表示系统模型的测量值和系统状态参量:
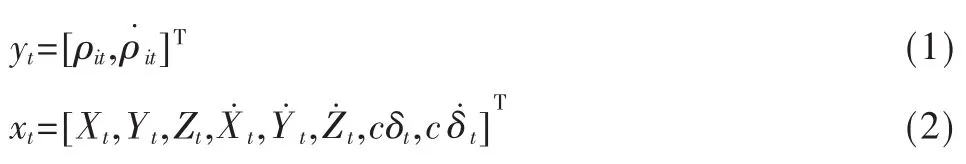
式(1)中,系统的测量值yt包括伪距ρit和伪距增量ρ˙it;式(2)中,系统状态参量xt包括接收机在地心地固(ECEF)坐标系下的位置(Xt,Yt,Zt)和速度(X˙t,Y˙t,Z˙t)以及光速c乘以时偏δt和光速c乘以时漂δ˙t8个参量。其中i=1,2,…,n,表示第i颗卫星(n为有效卫星数量),t为采样时刻。
1.1 测量模型
系统的测量模型描述了系统测量值与系统状态参量之间的关系。伪距与系统状态参量的关系可表示为:

式(3)中(Xit,Yit,Zit)为ECEF坐标系下的卫星位置,vρit为伪距的测量噪声。为了简化计算,一般伪距测量噪声vρit采用白噪声表示,且各通道之间的vρit相互独立。
伪距增量描述了卫星与接收机的径向速度,它与状态参量的关系可表示为:
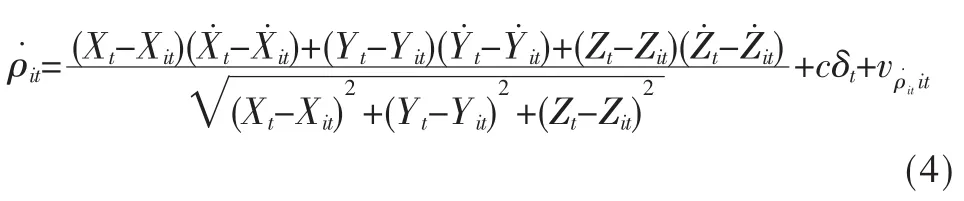
式(4)中(X˙it,Y˙it,Z˙it)为ECEF坐标系下的卫星速度,vρ˙itit为伪距增量的测量噪声。
综上所述,完整的测量方程为:

其中vt=[vρit,vρ˙it]T,i=1,2,…,n。在实际应用中,考虑到伪距和伪距增量的测量误差分别为米级、分米级,所以Vt的协方差矩阵R设为:

由于式(3)是非线性的,故而系统测量模型是非线性模型。扩展卡尔曼滤波(EKF)使用了低阶Taylor级数逼近非线性系统,在定位解算模型中主要体现在测量方程被近似线性化,即式(5)被写为:

式(7)中,Ht=∂h/∂x表示伪距测量值ρit和伪距增量ρ˙it对系统状态参量xt的偏导数矩阵。一般计算Ht矩阵(Jacobian矩阵)需在每个采样时刻得到一步预测值xt+1|t后重新计算,计算EKF算法公式中的Ht是对定位解算问题线性化的关键步骤。
1.2 状态模型
系统的状态模型描述了系统状态参量的时间更新过程。由参考文献[3-4]可知,更新过程的表达式为:

式(8)中的系数矩阵A、B为:

式(9)中的T为采样时间间隔。
式(8)中的wt表示系统状态转移的噪声模型:


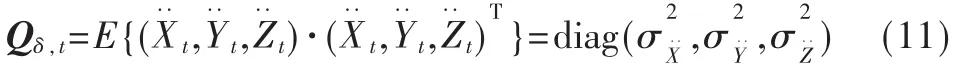
由参考文献[4]可以得到(wδ1,wδ2)的协方差矩阵为:

式(12)中,
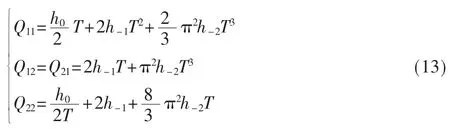
式(13)中的参数为:h0=9.4×10-20,h-1=1.8×10-19,h-2=3.8×10-21
综上所述,系统的状态模型的一步转移噪声wt协方差矩阵为:

2 改进的EKF
根据第1节中建立的系统模型,系统测量值yt为2参数,系统状态参量xt为8参数,为了得到准确解,故而需要至少4颗有效卫星的测量值。为了能够满足用户需求的定位精度,本文提出利用一般车辆行人等用户在垂直地面方向上的位置变化缓慢这一运动特性,增加如下方程:

式(15)中,Dt表示接收机在NED(以用户为中心,三个坐标轴N、E和D分别指向北、东和下)坐标系下D轴方向上的位置,D˙t表示在D轴上的速度,Dt+1|t、D˙t+1|t分别表示Dt和D˙t的一步预测值。对于在垂直地面方向上位置变化缓慢的用户,该方程均成立。
利用式(15),本文改进了扩展卡尔曼滤波(EKF)的时间更新过程。下面分两部分进行说明。
令用户在NED坐标下的八状态参量为:
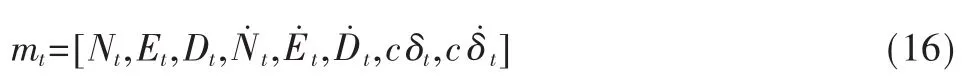
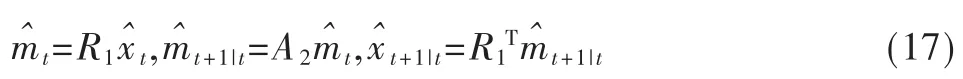
式(17)中,R1为从用户在ECEF坐标系下的状态参量xt到用户在NED坐标系下的状态参量mt的转换矩阵,利用坐标系旋转的原理可以求得[2]。A2为用户在NED坐标系下的状态参量mt的一步转移矩阵。它们的表达式如下:

根据参考文献[2]可知,式(18)中,

式(20)中λ为用户的经度,φ为用户的纬度。
易知R1为单位正交阵,故而用户从NED坐标系转换到ECEF坐标系时,转换矩阵即为R1T。
为了与普通的EKF进行对比,改进EKF使用的状态参量xˆt的自协方差矩阵Pt和系统的噪声协方差矩阵Qt仍为在ECEF坐标系下的初始值。那么状态参量的协方差矩阵Pt的时间更新过程如下:

式(21)中的系数矩阵为:

综上所述,并结合参考文献[5],得到改进的EKF算法的计算过程如下:
(1)初始化:

(2)时间更新:
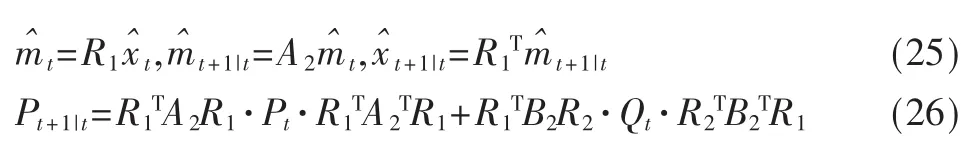
(3)测量更新:


根据理论分析可以得出,改进的EKF相对于普通的EKF来说,增加了一项先验信息,故而使得只有3颗有效卫星时的定位解算有了4个解算方程,因此可以相对准确地解算出4个未知数的值;而在有效卫星数不少于4颗时,增加的方程(15)仍然满足,故而也不会影响定位精度。
3 算法仿真和分析
在本文的算法验证实验中,使用了Leika GPS1200测量型接收机在车载动态下采集的GPS信号的伪距和伪距增量的测量值,其中伪距测量值经过伪距增量测量值的平滑。算法的验证是在PC机上使用Matlab完成的。
在算法验证中,设置采样时间间隔为T=1 s。接收机的运动状态为从静止状态变化到在地面上高速运动最后又逐步静止。测试数据长度为2 500 s。参考轨迹是接收机使用动态实时差分(RTK)方法测定的,方差精确至毫米级。分别在有效卫星不少于4颗和只有3颗的情况下,比较了几种定位解算算法的定位结果。
3.1 有效卫星数不少于4颗时的定位结果
以有效卫星数为4颗为例,分别使用ILS、EKF和改进的EKF算法进行定位,得到以ECEF坐标系下XYZ三维坐标表示的定位结果,如图1所示。
由图1可知,接收机在前400 s时基本保持静止,然后开始运动至1 600 s,最后逐步静止至测试结束。三种解算方法都可以较好地进行定位解算。为了更好地分析定位结果,画出图1中的XYZ三维坐标上的定位误差的均方根,如图2所示。


为了更好地比较ILS、普通EKF与改进EKF算法,计算图2中三种算法在XYZ三个坐标方向上的定位结果的均方根误差的平均值,如表1所示。
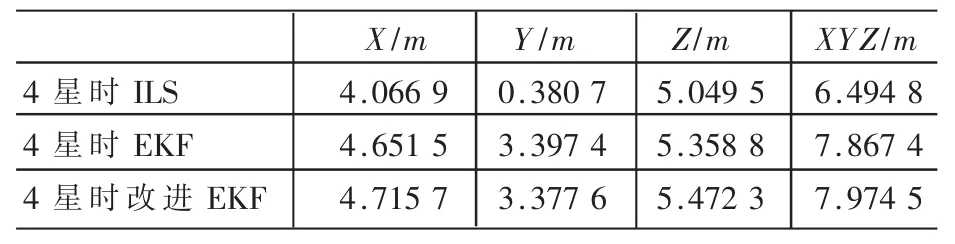
表1 三种定位结果的误差均方根的平均值比较
从图2和表1可以更清晰地看出,在有效卫星不少于4颗时,三种算法在以ECEF坐标系表示的XYZ方向上的定位误差的均方根均不超过20 m,平均定位误差不超过10 m,定位解算精度都很好。其中改进的EKF与普通EKF定位精度相当,而ILS的定位均方根误差抖动很小。这是因为,每当有新的测量数据时,ILS算法都会经过多次迭代计算直至结果收敛,而EKF与改进的EKF算法均只是利用新息进行一次计算,计算量要远远小于ILS,故而定位结果会稍有抖动。
3.2 有效卫星数只有3颗时的定位结果
在有效卫星数只有3颗时,ILS无法进行定位。分别使用普通EKF和改进的EKF算法进行定位,得到在ECEF坐标系下的XYZ三维坐标上的定位结果,如图3所示。

为了更好地分析定位结果,画出图3中的XYZ三维坐标上的定位误差的均方根,如图4所示。
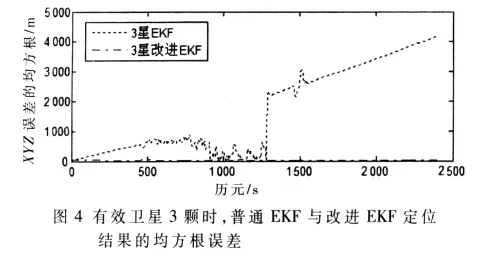
为了更好地比较普通EKF算法与改进EKF算法,计算图3中两种算法XYZ三维坐标上的定位结果的均方根误差的平均值,如表2所示。

表2 EKF与改进EKF的定位结果的均方根误差的平均值比较
由图3、图4和表2可知,在只有3颗有效卫星的情况下,普通EKF的定位结果会出现明显的偏移,而本文提出的改进的EKF算法的定位结果与参考轨迹拟合得很好,各个方向上的平均定位误差均不超过10 m,定位精度很好。这说明本文提出的改进EKF算法在只有3颗有效卫星时,极大地提高了EKF的定位精度。与理论结果吻合。
3.3 有效卫星为3颗时改进EKF与有效卫星为4颗时普通EKF的定位结果
为了进一步分析改进EKF算法的性能,将改进EKF算法在只有3颗有效卫星时的定位误差与普通EKF算法在有4颗有效卫星时的定位误差进行比较,如图5所示。

计算图5中的两种情况下XYZ三维坐标上的平均误差的均方根,如表3所示。
由图5和表3可知,在只有3颗有效卫星时,本文提出的改进EKF算法所增加的先验信息与增加一颗卫星的测量信息的效果基本一致。故而说明在出现GPS信号阻塞的情况下,只有3颗有效卫星时,此改进EKF算法的定位解算精度非常好。

表3 4星时普通EKF和3星时改进EKF的定位的平均误差均方根比较
综上所述,利用实测的卫星数据进行验证,结果表明:在3颗有效卫星的情况下,在静止状态和车载状态下,改进的EKF算法的定位精度均明显优于普通的EKF,且与4颗有效卫星时EKF的定位精度相当;在不少于4颗有效卫星的情况下,在静止状态和车载状态下,改进EKF算法的定位精度与普通EKF相当。由此说明,本文提出增加的先验信息在已有足够测量信息时,并不会影响定位精度,而只有在3颗有效卫星时,测量信息对于定位精度的改进与一颗有效卫星的测量信息效果基本一致,从而大大提高了EKF算法的鲁棒性。
本文在GPS信号出现阻塞,有效卫星数降为只有3颗时,改进EKF算法以提高GPS定位解算精度,并使用真实卫星数据对改进的EKF算法进行了验证。实验结果表明,在有效卫星不少于4颗时,本文提出的改进EKF的定位精度与EKF相当。在GPS信号阻塞,有效卫星数只有3颗时,改进EKF的定位精度明显优于普通EKF,且与4颗有效卫星时EKF的定位精度相当。受本文算法改进中所引入的先验信息的限制,本文提出的改进EKF算法适合车载等地面运用,不适合在垂直地面方向上高速运动的情形。
参考文献
[1]COOPER S,DURRANT W H F.A kalman filter model for GPS Navigation of Land Vehicles,IEEE Conference on Intelligent Robots and System(IROS’94),Munich,Germany,1994(11):12-16.
[2]MISRA P,ENGE P著.全球定位系统——信号、测量与性能(第二版).罗鸣,曹冲,肖雄兵,等译.北京:电子工业出版社,2008:103-106.
[3]AGOGINO A,ALAG S,GOEBEL K.Intelligent sensor validation and sensor fusion for reliability and safety enhancement in vehicle control,MOU132,UCB-ITSPRR-95-40,California PATH Ressarch Report,1995.
[4]KEE C,PARKINSON B W.Wide area differential GPS.Navigation:Journal of The Institute of Navigation.1991,38(2).
[5]曹洁,文如泉.非线性滤波算法在机动目标跟踪中的研究[J].信息化纵横,2009,28(18):61-64.

