导弹中末段制导导引律转换研究*

赵 东 蔡海超 赵海涛

(海军装备部驻上海地区军事代表局1) 上海 201206)(92721部队2) 舟山 316000)

1 引言

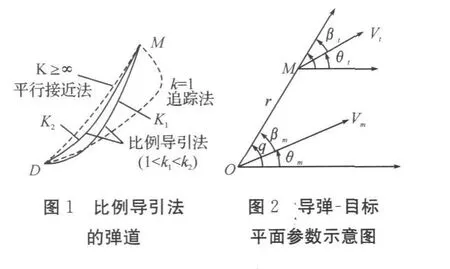
反舰导弹在飞行过程中,常用的经典导引方法有追踪法、平行接近法和比例导引法等。其中追踪法分为纯追踪法和常值前置角追踪法,这两种方法都存在比较严重的缺陷,即使在拦截非机动目标时,也不能保证直接命中。平行接近法是一种理想的导引方法,然而平行接近法需要精确已知目标的飞行状态,在实际中实现十分困难。比例导引是一种介于追踪法和平行接近法之间的制导方法,拦截非机动目标时弹道性能好,脱靶量小,而且易于工程实现,因此受到普遍重视。然而当存在目标机动,特别是当目标法向机动过载接近甚至大于导弹法向过载能力时,单纯的比例导引律的性能会大大下降,即导弹法向过载过早饱和,终端脱靶量很大[1]。

为弥补纯比例导引带来的缺陷,文章对比例导引法进行系统分析,研究并提出了一种带有修正和可变系数的比例导引律,这种导引律综合了平行导引律和追踪法导引律的优点,避免了固定系数比例导引律的缺点,最后建立仿真模型,对该比例导引律的优点进行了验证。

比例导引法具体有三种方式,即追踪法、平行接近法和比例导引法。其中追踪法是指导弹在攻击目标的导引过程中,导弹的速度矢量与导弹、目标连线(视线)重合。这种导引方法一般用于攻击低速或静止目标的导弹,或向目标尾部发射的情况;平行接近法要求在制导过程中始终保持目标视线在空间沿给定方向平行移动,即视线角速度为零。按平行接近法导引时,导弹速度矢量每一时刻都指向瞬时遭遇点,因此,平行接近法也叫瞬时遭遇点法。用平行接近法导引时,由于保持目标视线与基准线的夹角为常数,如保持导弹速度矢量前置角不变,则导弹的弹道就为一条直线。所以在目标做直线运动情况下,用平行接近法导引时,只要速度比保持常数(k＞1),导弹从任何方向攻击目标,都能得到直线弹道。

比例导引法要求导弹飞行过程中,保持速度矢量的转动角速度与目标视线的转动角速度成给定的比例关系,导引方程为:θ′=kq′,式中k为导引系数,也称导航比;θ为导弹飞行弹道角;q为弹目视线角。另外,采用比例导引法时,弹道初始段和追踪法(k=1)相近,弹道末段和平行接近法(k=∞)相近。导弹的理想弹道的曲率介于平行接近法和追踪法之间。追踪法导引时弹道曲率最大,导弹的速度矢量时刻指向目标,这种导引方法在导弹接近目标的时候会带来极坏的弹道特性,使过载很大。但是考虑到导弹中段飞行中,距离目标比较远,因此目标的机动对导弹弹道影响比较小,因此这段时间内是可以采用追踪导引律的,以便于快速接近目标。在末段时,由于目标机动、导弹变速飞行,适当提高导引系数k,导弹转换制导律,这样导弹的飞行弹道曲率会变小,导弹需用过载降低。但k值不是越大越好,如果k值很大,即使q′不大,也可能使导弹的需用过载很大[2]。为了保证满意的视线角速度,比例导引系数存在最优取值范围,即k=3～6[3],这里取k=4。由于中间段可采用有效比例导航系数k=1的比例导引系数,末段可采用k=4的比例导引系数,所以本文结合追踪法和比例导引法,提出了一种可变导引系数的比例导引法。

2 可变系数的比例导引法

2.1 弹道衔接

本文中导弹采取串联式复合制导方式,在中段向末段的过渡过程中,导弹导引律的导引系数将产生变化,因此存在由一种制导方式向另一种制导方式的过渡问题,这种过渡是由一种引导方法向另一种引导方法的转变,由于引导方法的突变,必然引起弹道轨迹的折损,以至不能击中目标.因此,弹道的衔接和过渡显得尤为重要。要保证两段弹道在过渡点处吻合必须满足一定的条件。设导弹在弹道i处的加速度为ai,在弹道j处的加速度为aj。那么两段弹道在交接点处吻合的条件为:

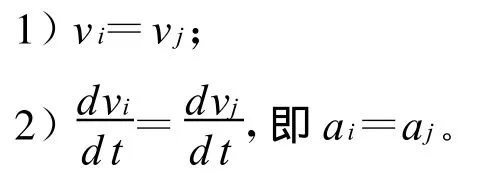
2.2 弹道方程

描述导弹质心运动和绕质心运动的数学模型是将导弹视为刚体的六自由度动力学模型,是一个非线性、变参量的数学模型,包括姿态角、攻角、侧滑角、舵偏角和随机干扰在内的大量参数,一般做法是依据具体情况将之逐渐简化以求得闭合解。通常情况下,导弹是在三维空间内运动的,平面运动只是导弹运动的一种特殊情况。在某些情况下导弹的运动可近似地视为在一个平面内,例如地-空导弹在许多场合是在铅垂面或倾斜平面内飞行;飞航式导弹在爬升段和末制导段也可近似地认为是在铅垂平面内运动;空-空导弹的运动,在许多场合也可看成是在水平面内。所以在导弹的初步设计阶段,研究、解算导弹的平面弹道是具有一定应用价值的。本文将导弹的运动进行解耦,并放在一个平面内进行研究,把实际三维问题转化为两个互相垂直平面上的二维问题。

选取惯性坐标系的垂直平面和水平面为两个独立的研究平面。在这里将导弹和目标放在垂直平面内进行分析。导弹截击目标的平面图如图2所示,图中水平线为参考线,Vm为导弹的速度,Vt为目标速度,q为弹目视线角,βm为导弹的前置角,βt为目标的前置角,θm 为导弹的飞行弹道角 ,θt为目标的飞行航迹角,r为目标和导弹间的相对距离。为研究导弹与目标之间的相对运动方程,将导弹运动速度矢量和目标运动速度矢量分别沿着相对距离r方向和其法线方向分解成两个分量。沿r方向的分量为vmcosβm,vtcosβt,沿法线方向的分量为 vmsinβm,vtsinβt。根据速度分量表达式,求得导弹-目标之间的距离变化率dr/dt为:

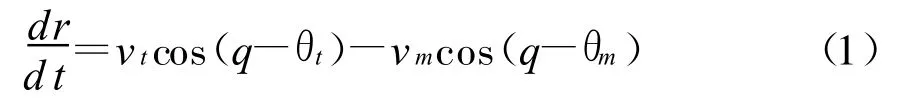
距离旋转角速度的变化率为:

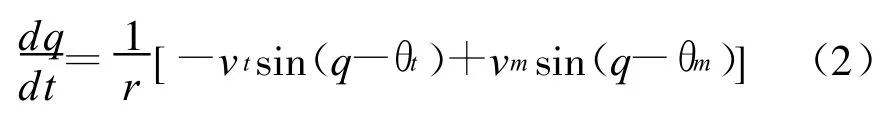
利用相对运动关系和导引方程,可以得到以下方程组:

再根据以下导引律:

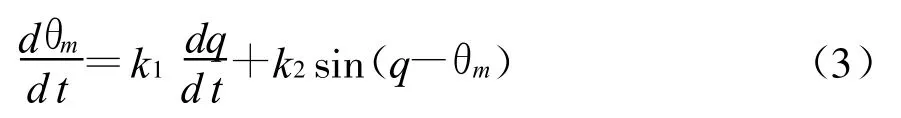
其中,vt,vm,θm已知。式(3)中右边第一部分相当于比例导引,第二部分作为修正量,作用相当于追踪法导引[3]。为了简化研究过程,这里取

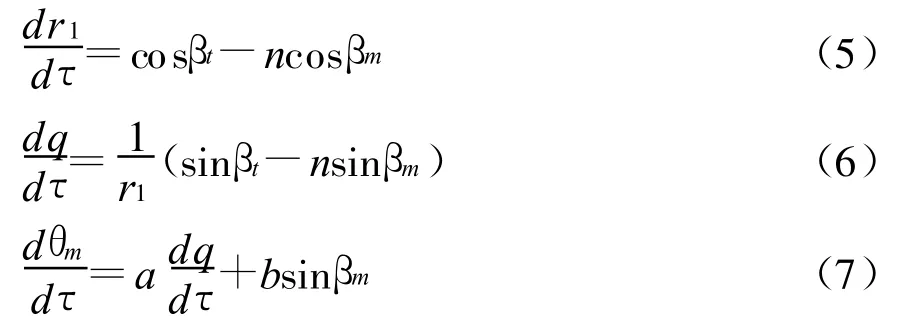
在τ域中,导弹法向加速度为

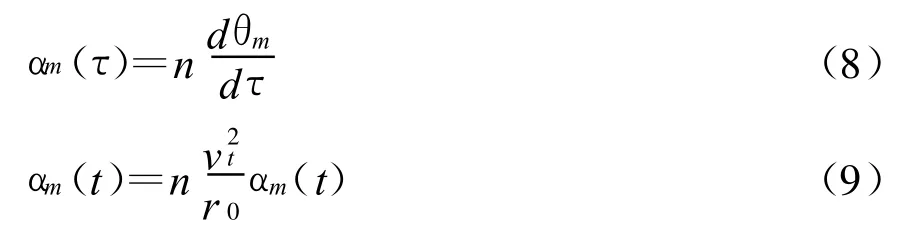
目标的法向加速度为

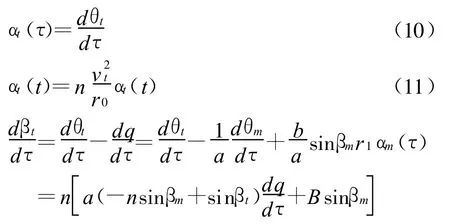
从这一导引律可以得到

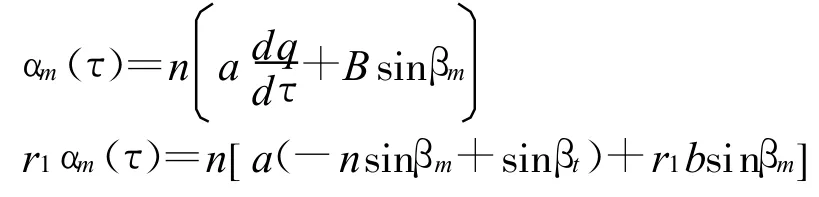
又因为 θm=βm+q,有

对方程两边对τ求导数,变换得到

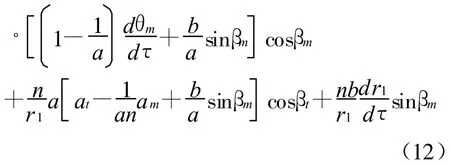
以上方程(5)～(12)构成了组合末制导系统的解析解表达式[4]。

弹道平滑过渡问题实际上就是由k1=1到k1=4的过渡问题。假设在时间t0处开始过渡,3s(t＜3s)内完成由k1=1到k1=4的过渡,这样在过渡段内k1的表达式为:

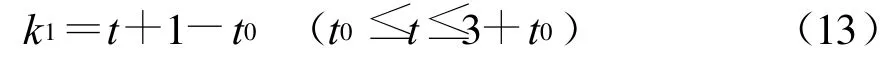
当t＞3s以后保持k1=4。由于导弹开始由中段向末段制导转换的交接点处,导引系数k没有发生变化,因此弹道是满足吻合条件1的。要满足二阶平滑过渡,需要求弹道倾角的变化率在过渡点处相等[5]。

3 仿真分析

导弹制导系统的导引头,无论是雷达头还是红外头,他们都有一定的最小测量距离(几十米或几百米),当导弹和目标接近到这个距离之后,导引头就停止正常工作,控制系统从此依其过渡过程恢复到平衡位置,导弹同时将根据控制舵的位置作直线弹道或曲线弹道飞行。导弹绕过目标的最小距离,称之为脱靶量。

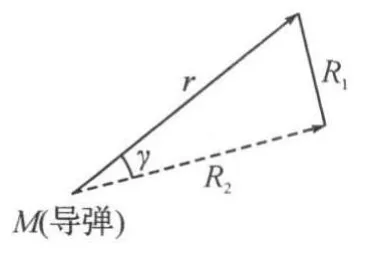
图3 脱靶量的平面几何表示

下面我们分别根据舵在导弹运动最后瞬间是否处于中间位置,来讨论脱靶量的计算公式。设导引头停止工作时刻为ts,相对距离为rs,视线角速度为qs,考虑到导弹任意机动,在平面情况下,脱靶量由横向偏差(垂直于LOS)和纵向偏差(平行于LOS)两部分组成。

3.1 目标与导弹均作匀速飞行

设导弹飞行速度为Vm,目标速度为Vt,R1为导弹径向飞行距离,R2为导弹横向飞行距离,t为弹目相遇时导弹飞行时间。根据余弦定理可以得到:

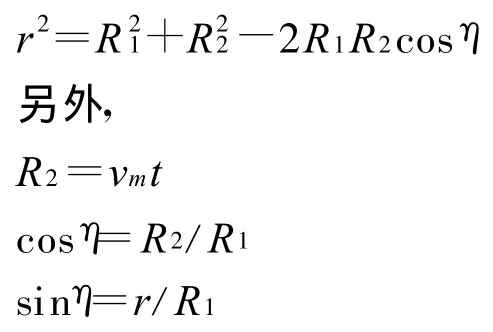
根据比例导引律公式可以得到

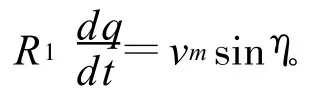
因此

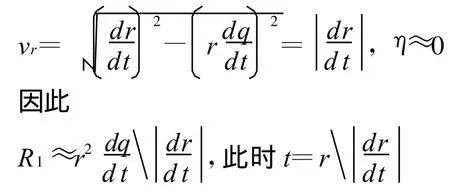
3.2 导弹目标作变速运动

在实际情况中,导弹目标经常采取变速运动飞行,且有横向机动,可近似认为此种条件下脱靶量为:

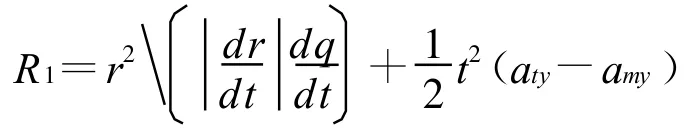
其中,amy和aty分别为导弹和目标的加速度在视线法向的投影,表达式为

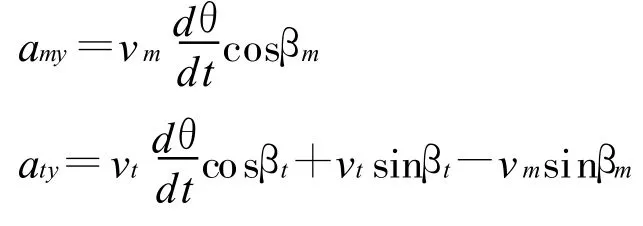
3.3 脱靶量分析

假设目标作正横向机动飞行,Vm=800m/s,Vt=340m/s,at=80m/s2,am=0m/s2,r0=3000m,βt=-90°,βm=-38°,θt=17°,θm=70°。当 b=3 时,目标加速度取不同值时,导弹采用比例导引(a=1,a=3)和组合导引以及变系数导引方式的脱靶量比较如表1所示。

表1 比例导引和组合导引仿真结果比较

3.4 弹道分析

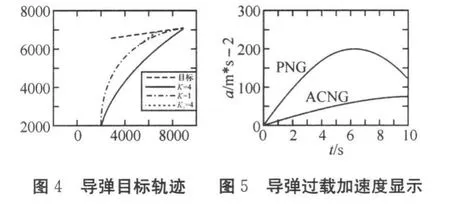
假设导弹起点位置为(2000,0),目标作直线运动。图4描述了当k=1,k=4,以及中末端交班采取可变系数(k=1,k1=4)的三种比例导引律的情况,图4表明弹道衔接过渡平滑,并且缩短了弹-目相遇时间,图5表示导弹在整个相遇过程中,明显降低了需用过载。

4 结语

本文对纯比例导引法入手,提出了一种新型的组合制导律。通过数字仿真结果可以看出,本文提出的组合制导律充分吸收了比例导引系数在不同取值时弹道特性的优势,消除了固定比例导引系数的缺点,在对付机动目标可以大大降低过载和脱靶量。因此,这种制导律在实际运用中是十分值得推广运用的。但是,导引系数仍然是影响该比例导引法优劣的关键因素,因此更进一步讨论导引系数的取值是非常有必要的。另外,对于弹道交接时间的可行性也是需要在实际运用中解决的问题。

[1]程国采.战术导弹导引方法[M].北京:国防工业出版社,1996

[2]孟秀云.导弹制导与控制系统原理[M].北京:北京理工大学出版社,2003

[3]刘兴堂.精确制导、控制与仿真技术[M].北京:国防工业出版社,2006

[4]张合新,孟飞,汪立新.组合末制导律及其仿真研究[J].火力与指挥控制,2003(1):33～36

[5]罗喜霜,张天桥.多用途导弹中末段交班研究[J].弹道学报,2001(4):47～50

[6]陈佳实.导弹制导和控制系统的分析与设计[M].北京:宇航出版社,1989