基于变权重的多因子来袭导弹威胁评估*

孙一杰 曾 静 杨先德

(第二炮兵工程学院 西安 710025)

1 引言

为了提高常规导弹阵地的生存防护能力,首先必须对阵地面临的威胁进行准确、有效、及时的评估。战场环境瞬息万变,在一场战役中,一方不可能时刻保持绝对优势,很可能由于指挥员决策等其他多种因素的影响而导致战场态势发生变化。如果不顾实际战场环境而不断改变对战场态势的判断,就容易因脱离实际情况而导致作战时机的失去,造成更严重的后果。本文采用变权重的多因子来袭导弹威胁估计,可以实时地根据战场态势来重新确定各个威胁要素的权重值,并提出了不同威胁等级的防护对策,增加战场威胁估计和处理的科学合理性。

2 基于变权重的多因子来袭导弹威胁估计

导弹攻防对抗作战威胁估计一般包括:威胁要素提取、威胁合成和威胁等级确定三个部分。理想的威胁评估方法应该是原理直观,计算步骤简便且容易实现,应从问题的本身出发,充分利用目标的实时信息,正确选取及组合威胁指标,以恰当的模型和计算方法来对空袭目标进行威胁评估。3级融合威胁估计的功能结构如下[1]:

2.1 威胁要素的提取

在现实作战过程中,影响目标威胁的因素有很多,很多情况下,各个威胁因素都可能是不清晰或半透明的,一般是很难完整建立的。针对导弹攻防对抗作战过程的威胁评定,只需要把主要因素考虑进去即可,而不去考虑其他一些比较次要的因素,在本文中,主要考虑的因素有:1)来袭导弹接近目标剩余时间;2)欲打击目标的抗毁伤能力;3)来袭导弹的突防方式;4)来袭导弹的数量;5)防御方反导防御系统的性能。

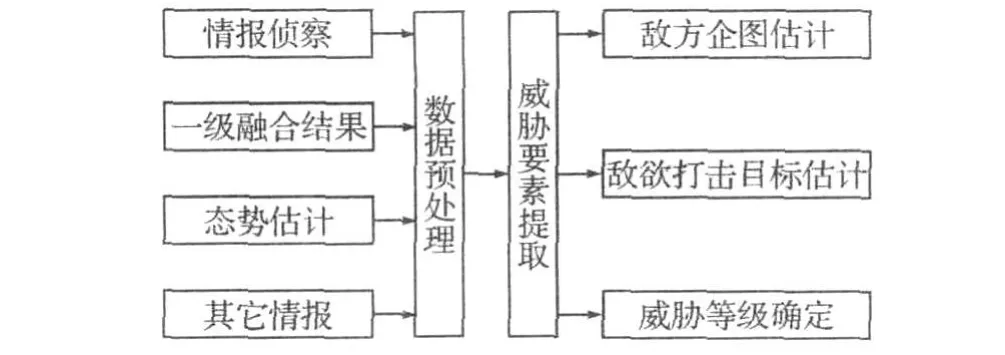
图1 威胁估计功能结构图

2.2 隶属度函数及威胁要素分析[2～3]

1)来袭导弹接近目标剩余时间

当来袭导弹飞向欲攻击目标时,到达时间越短,威胁程度就越大,剩余时间威胁隶属度函数可选取偏小型隆半正态分布函数形式;当目标飞离目标时,到达时间可认为是负值,绝对值越大,威胁度越小,此时隶属函数可取隆半柯西分布函数。则威胁隶属度函数为:

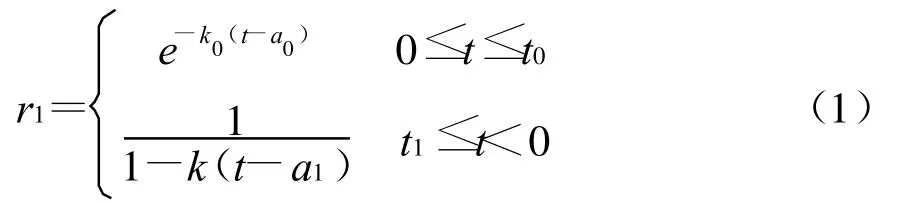
其中 k0、k1、a0、a1为系数,可根据实际战场情况确定。

2)来袭导弹的数量

由于防御方反导系统的拦截导弹能力是一个定值,因此,当来袭导弹的数量超过反导系统的最大拦截能力,进行饱和攻击时,来袭导弹对防御方的威胁程度将变得很大。根据这一思想,本文确定来袭导弹数量对防御方的威胁隶属度函数为:

其中,k为系数;n是防御方反导防御系统的最大拦截能力;x是攻击方来袭导弹数量。

3)来袭导弹的突防技术、来袭导弹的弹头威力、防御方导弹防御性能的威胁度量化值如表1～表3所示。

表1 突防技术威胁度量化值

表2 抗毁伤威胁度量化

表3 导弹防御威胁度量化值

2.3 基于变权重的导弹作战威胁估计

2.3.1 变权的基本理论

李洪兴在汪培庄教授提出的变权思想的基础上,根据因素空间理论对变权原理进行了深入讨论,给出了变权的公理化定义[4～5]:

变权是下述m个映射wj(j=1,2,…,m)

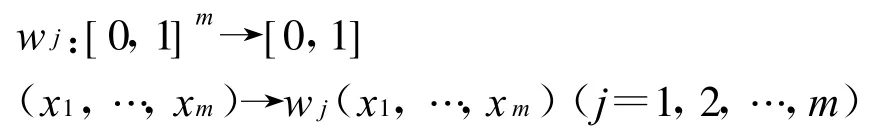
满足下面三条公理:

1)归一性;2)连续性;3)惩罚性。

通过分析变权的原理,可以得到以下结论:

1)变权重向量W(X)=(W1(X),…,Wm(X))可以表示为因素常权向量和状态变权向量S(X)的归一化的乘积:

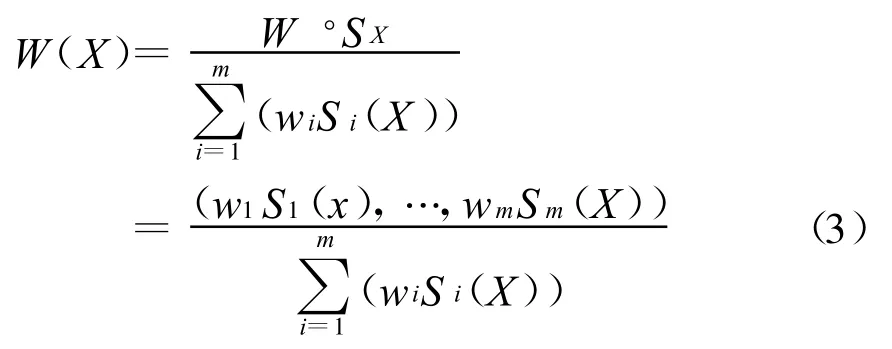
2)状态变权向量S(X)是某个m维实函数的梯向量,它反映了各因素状态的一阶变化情况:

2.3.2 变权重的导弹作战威胁估计

由前面分析及根据实时性要求,对来袭导弹的弹头威力、防御方反导防御系统的性能、来袭导弹的突防方式的权重采用比较简单的一阶线性函数,表达式如下:

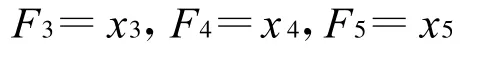
分析实际问题可知,当来袭导弹剩余时间越来越少时,F1取值基本上是线性增加,当来袭导弹很接近防御目标时,即剩余时间t的值很小时,其t微小的变化都会显著影响威胁值。所以,对剩余时间的变权函数选择了线性函数加上对数函数的形式如下:

其中,α为调整因子。根据实际战场情况确定。

来袭导弹数量对防御目标的威胁度函数为:

其中:μ为调整因子,β＞0,x2为来袭导弹数量。

综合以上各式得到综合函数为:

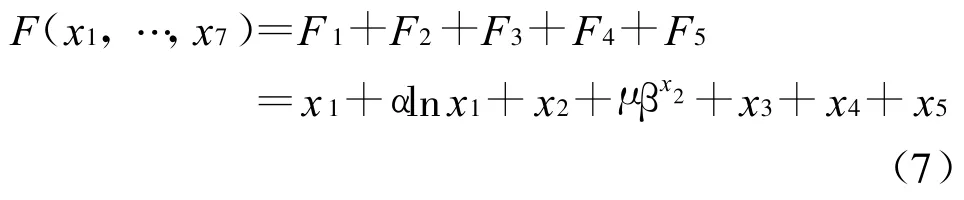
由式(4)可求得状态变权向量:

其中,当j=3,4,5时,Si为常数,表示其威胁因素对应的权值不随xi的变化而变化;当j=1时,S是一个单调递减函数,其权值随着时间的减小而增大,表示对防御目标的威胁度变大,符合实际作战情况;当j=2时,S是一个单调递增函数,其权值随着来袭导弹数量的增加而增大,对防御目标的威胁度也相应增大,符合实际作战情况。

当S1,S2变大时,根据可知,其他几个对应的权值应当相应变小。通过归一化Hadamard乘积公式,求得实际作战过程中,各威胁因素实时的权重值为:

其中,wi(i=1,…,5)为各威胁因素的初始权重值。wi为根据实时作战进展变权后的权重值。

通过以上分析,可以得出变权综合函数:

2.4 常规导弹阵地防护决策[6]

对某一常规导弹阵地而言,可以按照来袭武器的威胁度值和阵地属性建立威胁等级及相应的生存对策。从而提供有效快速的防护辅助决策依据阵地面临的威胁程度,可以分为以下级:一级为轻度威胁,威胁度值[0,s1];二级为较大威胁,(s1,s2];三级为重大威胁,(s2,s3];四级为严重威胁,(s3,s4];五级为致命威胁,(s4,+∞)。具体数值针对导弹阵地情况可由专家综合评估得到。同时建立了与威胁等级相对应的生存对策见表4。

表4 生存对策

3 算例分析

为了验证变权重的导弹作战威胁评估的有效性,现选取实例进行仿真分析。

在某次战役中,攻击方(甲)由于某种战略需要,用4枚某型地地常规导弹对防御方(乙)某阵地进行攻击,并将根据实时情况适当增加常规导弹攻击数量,为了突破防御方较强导弹反导防御系统,攻击方导弹采用假弹头(诱饵)技术、多弹头技术和机动变轨技术突破对方的反导系统。假设防御方反导系统在一定的时间内最大能够拦截6枚来袭导弹,来袭导弹距离防御方目标的剩余时间为20min。

根据前面隶属度函数及其威胁要素分析,对各威胁要素进行取值如下所示:

剩余时间的威胁因素量化值由式(1)可求得:

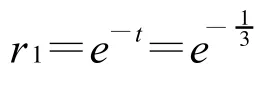
其中:k0取值为1,a0取值为0;t为来袭导弹距欲打击目标的剩余时间。

来袭导弹数量的威胁因素量化值由式(2)可求得:

其中:k2取值为0.5。

其余各威胁因素量化值:r3=0.5,r4=0.5,r5=0.5

各威胁因素的初始权重值:w1=0.16,w2=0.20,w3=0.22,w4=0.24,w5=0.18

来袭导弹剩余时间变化后,经过变权重公式处理后,各个威胁因素的权重值如表5所示。

通过实际计算可以发现,当来袭导弹的剩余时间越少,其所对应的权重变得越大,并且在后期,微小的时间变化就会引起其权重值的剧烈变化。而当来袭导弹被防御方反导系统拦截减少时,其导弹数量所对应的权重值也变小,通过以上实际计算可以清楚地显示变权重的有效性。

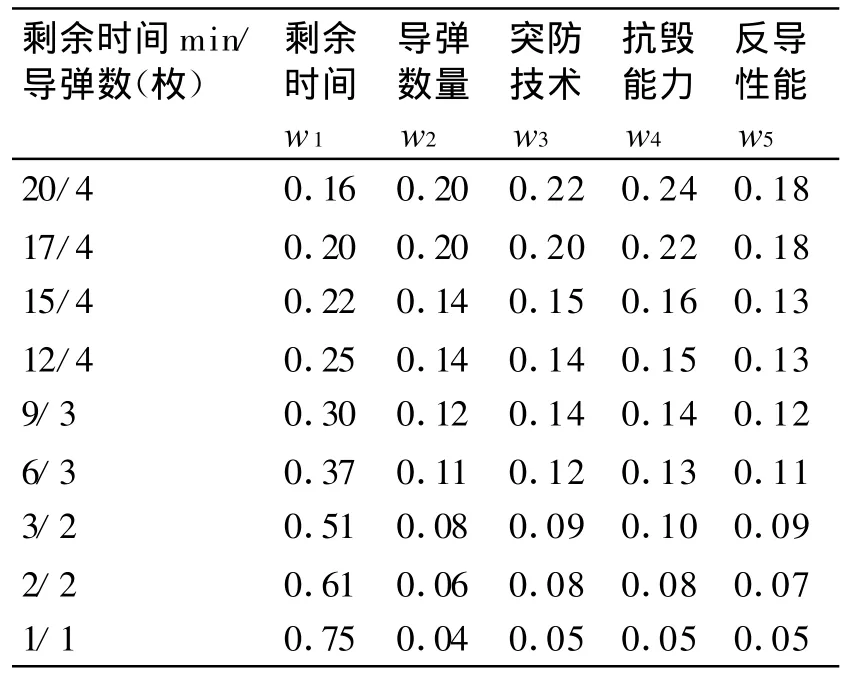
表5 威胁因素权重值

表6 威胁度变化值

4 结语

面对境瞬息万变的战场态势,如何在众多信息中快速有效地提取有用的信息,为指挥员提供决策参考,是战争能否取得胜利的关键环节。本文采用变权重的多因子来袭导弹威胁估计,可以实时地根据战场态势来重新确定各个威胁要素的权重值,增加战场威胁估计和处理的科学合理性。在威胁等级确定之后,根据各威胁等级的特点制定了相应的对应措施,从而为决策者提供有效快速的辅助决策依据。通过仿真实例说明了该算法的有效性,能够很好地反映战场的真实情况。

[1]罗小明,等.弹道导弹攻防对抗的建模与仿真[M].北京:国防工业出版社,2009,1

[2]张肃.基于灰色关联度分析的目标威胁程度评估[J].制导与引信,2005,26(3):19～23

[3]梁百川.对抗NMD/TMD的技术[J].航天电子对抗,2006,22(1)

[4]汪培庄.模糊集与随机集落影[M].北京:北京师范大学出版社,1985

[5]李洪兴.因素空间理论与知识表示的数学框架(Ⅸ)—均衡函数的构造与Weber-Fechner特性[J].模糊系统与数学,1996,10(3):12～19

[6]邓鹏华.基于证据理论的常规导弹阵地生存防护研究[J].海军工程大学学报,2006,18(5):110～112