基于SVD和小波变换的信道估计新方法
喻永华,宋学瑞
(中南大学 信息科学与工程学院,湖南 长沙 410083)
近年来正交频分复用系统(OFDM)得到了广泛的应用。其基本原理是将高速的数据流分解为多路并行的低速数据流,在多个载波上同时进行传输。数据流的串并转换有利于实现多种调制和变换以及保护间隔的加入,达到在不同无线信道中传输的要求。在OFDM系统中,信道估计是研究的热点之一,是进行相干检测、解调和均衡的基础。
本文针对快慢衰落含噪无线信道提出了一种新的信道估计方法。它采用梳状导频子载波排列,将LS算法与小波变换相结合,然后对变换后的结果进行奇异值低阶近似。导频子载波中的加性噪声经小波变换中的阈值处理后,再对其转移矩阵进行低阶近似。通过仿真可以发现,地板效应得到良好的改善。
1 基于导频的OFDM信道估计
一种基于梳状导频信道估计的OFDM系统如图1所示。假设OFDM系统中,每个OFDM符号的子载波总数为N,L为多径信道的径数,其中共有M=N/L个导频子载波,N-M个信息子载波,二进制信息数据经过调制后均匀插入导频,频域信号可以表示为:

接收端的时域信号yg(n)可以表示为:

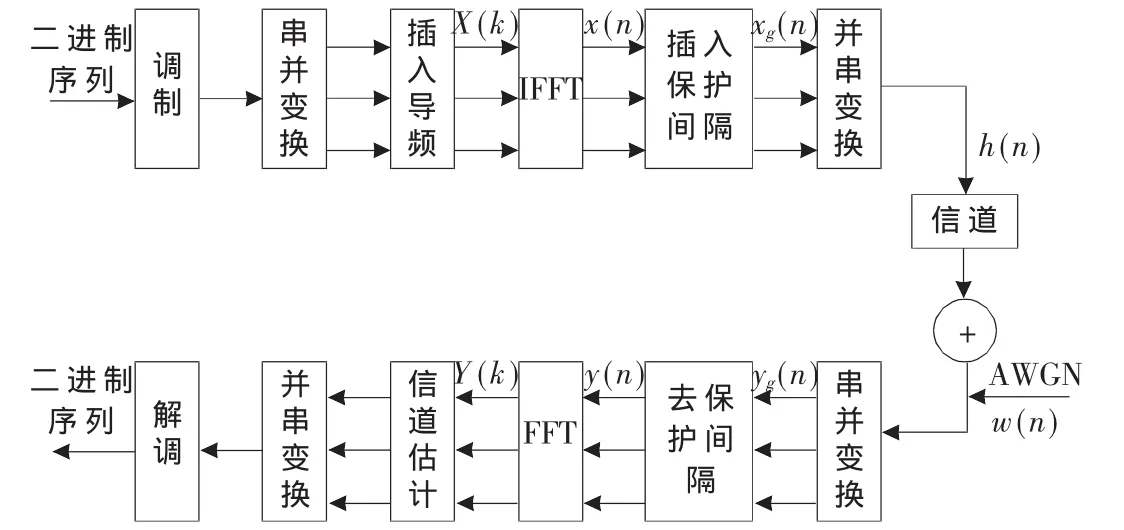
图1 OFDM系统框图
式中,w(n)为加性高斯白噪声,去掉保护间隔后的信号为y(n),y(n)经过快速傅里叶变换 FFT得到频域信号 Y(k)为:

式中,W(k)为 w(n)的傅里叶变换,H(k)为信道传输函数在第k个子载波上的响应,与传输信号相互独立。信道估计的目的是从接收到的导频信号中估计H(k)。
2 信道估计新方法
本文提出了一种基于小波去噪和奇异值分解的低阶近似MMSE信道估计算法,其信道框图如图2所示。LS算法的估计结果经过小波去噪后,再利用奇异值分解算法对信道转移矩阵函数进行低阶近似。仿真结果说明了本算法在大量减少计算量的前提下,其性能与只用了低阶近似[1]算法相比有了一定提高,而且本文通过采用梳状导频估计,与参考文献[2]算法相比更接近真实情况,此外,因为采用了奇异值分解,所以克服了参考文献[2]算法近似阶数不能改变的缺点。

图2 结合小波去噪的信道框图
2.1 基于LS的小波去噪
最小平方(LS)算法是最简单的一种信道估计算法,它的目标是:

由正交性原理,可得LS估计:


当信噪比较低时,噪声的影响将会加大,此时可以用小波去噪对LS估计后的结果进行去噪。去噪过程如下:首先对LS估计的信道进行小波分解,假设进行两阶分解,如图3所示;然后利用门限值对含噪的小波系数cD1、cD2进行阈值处理;最后对信号进行重构,达到了消除噪声的目的。

图3 信号小波分解图
2.2 基于奇异值(SVD)的信道估计
信道冲激响应矩阵自相关函数的奇异分解:

式中,U为包含奇异向量的酉矩阵,∧为包含奇异值λ1≥λ2≥…≥λN的对角矩阵。最佳秩P的估计器推导如下:
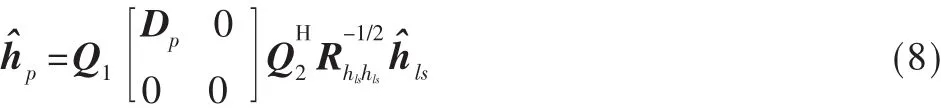
式中,Q1、Q2为酉阵,DP为对角矩阵的 P×P阶左上角矩阵。在块状导频的情况下,可以将上式简化为:

从式(1)可以看出,计算量从原来的N阶变为P阶。阶数为P的低阶信道估计器原理如下:首先,接收信号乘以X-1得到LS信道估计值hˆls,然后进行小波去噪。低阶估计器可以看作是将去噪后得到的值映射到阶数为P的子空间以降低噪声的影响,然后再变换为频域。如果子空间的维数很小,而且能够很好地描述信道的特性,则可以得到复杂度很低且性能很好的信道估计器。
同时必须看到,低阶估计器在带来一系列好处的同时,也有不可避免的缺点。由于只在信道的子空间进行估计,所以会引入一定的估计误差。一般在阶数P近似等于循环前缀长度的时候可以得到很好的信道估计器,而在OFDM系统设计时[3],通常要求循环前缀的长度要远小于OFDM符号长度,所以运算的复杂度可以大大降低。
下面讨论阶数为P的低阶估计器的均方误差MSE[4]。

由式(10)可知:基于奇异值分解的低阶近似 MMSE算法的均方误差只由LS的估计值、估计器设计时信道相关矩阵和信噪比与实际情况的匹配程度决定,与其他因素无关。所以当采用小波去噪对LS估计结果进行改善后,再进行MMSE估计时,其地板效应会得到改善。在仿真条件(子信道个数为 64,符号周期为 138 μs,循环前缀为 10 μs即 5个符号,近似阶数为 8)下,其计算机仿真如图4所示。
3 仿真结果及分析
采用系统带宽为1 MHz,载波频率为 1 GHz,子信道个数为512,其中导频信道为64,导频方式为梳状,循环前缀为16,信道为典型Rayleigh信道并假设多径全部位于循环前缀持续时间中,信号为16QAM调制。选用消失矩为8的daublchies小波对LS估计信号进行2层小波分解并去噪,然后进行阶数为20的低阶近似,插值方式为一阶线性插值[5-6]。均方误差及误码率仿真结果如下:

图4 本文算法与参考文献[2]算法的地板效应比较
(1)均方误差随信噪比变化的仿真曲线如图5所示。由于LS算法对噪声比较敏感,所以在信噪比较小的情况下,LS算法有较大误差。用本文算法对LS信道估计结果进行小波变换后,再用SVD算法进行低阶近似,在近似阶数均为20的前提下,相对于LS算法有很大的改善。
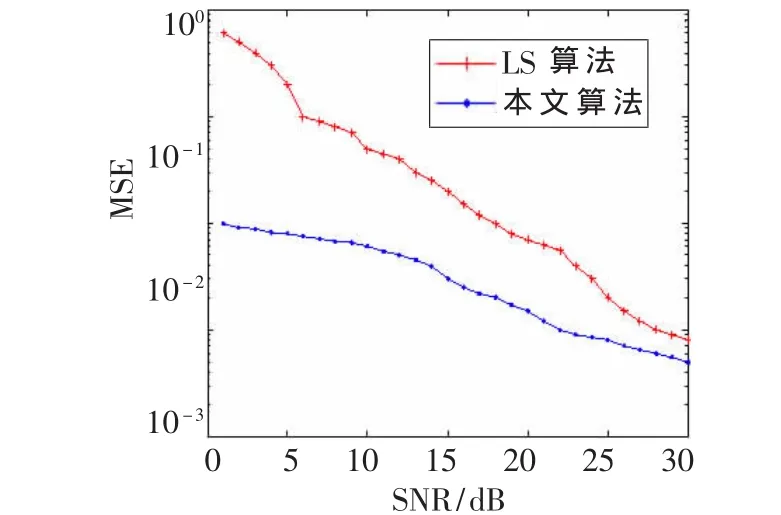
图5 均方误差曲线图
(2)误码率随信噪比变化的仿真曲线如图6所示。由图可见,本文算法比LS算法有较大改善。
本文将小波去噪方法与奇异值低阶相结合,对传统的LS算法信道估计进行了一定的改进,有效地提高了信道估计的准确性和系统性能。同单一的SVD分解、DFT低通滤波的信道估计方法相比,其不需要已知系统的任何信道信息,具有一定的实际应用价值。由于系统的去噪性能取决于小波去噪方法的系数选择,如合适的小波基函数和分解函数,如何在不同的信道下选择合适的小波去噪参数,以及它们之间的关系将是下一步的研究方向。

图6 误码率曲线图
[1]张继东,郑宝玉.基于导频的OFDM信道估计及其研究进展[J].通信学报,2003,24(11):116-124.
[2]石慧,卓东风.OFDM系统中一种新的变换域信道估计方法[J].太原科技大学学报,2006,27(5):90-114.
[3]佟学俭,罗涛.OFDM移动通信技术原理与应用 [M].北京:人民邮电出版社,2003.
[4]BOGGESS A.小波与傅里叶分析基础[M].北京:电子工业出版社,2002.
[5]GIANNAKIS G B,HUA Ying Bo,STOIEA P,et al.无线通信与移动通信中信号处理研究的新进展[M].北京:电子工业出版社,2004.
[6]樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2003.

