一种改进的Snake模型图像分割算法
张 辉,吴月宁
(1.咸阳师范学院 数学与信息科学学院,陕西 咸阳 712000;2.西北农林科技大学 理学院,陕西 杨凌 712000)
图像分割是图像处理领域的一个基本问题,一直是图像处理中的难点之一,也是从处理到分析的关键。常用的分割算法大多出现边界不光滑、不连续以及与背景连成一片等问题。而Snake模型能够利用图像局部与整体信息,实现边界的准确定位,并能得到封闭的轮廓。自1987年Kass等人提出Snake模型后[1],Snake模型成为近些年专用于目标轮廓提取的一种主流模型[2]。
传统的Snake模型也存在着不少缺点,如结果对初值的依赖性强、容易收敛到噪声点、对复杂区域不能收敛到边缘且计算速度慢等。针对这些缺点,很多研究者做了有益的修正和改进。其中,EVIATAR H等[3]人提出的简化Snake模型使收敛范围有一定扩大,但计算面积能量要对顶点连线作出是否交叉的判断。王元全等[4]人提出的构造曲率力思想使得轮廓点收敛到深凹陷区域,但该力的引入需要对轮廓点进行凹凸性判断,而轮廓点的凹凸性往往很难做到有效判断。
本文将传统Snake模型不能收敛凹陷区域归结为在内部能量中。内部力的不足,在参数个数不增加的前提下对内部能量增加内部力,并对改进后的Snake模型采用分段计算的Greey算法。使改进后的Snake模型较好地收敛到凹陷区域且抗噪性有所提高、结果对初值的依赖性减弱,适合复杂区域的图像分割,而参数个数未增加且易调整,同时算法的实现无需对轮廓点的性质进行判断,实现简单。
1 传统Snake模型
Snake模型是一种可形变模型(弹性模型),原始的Snake 是由一组轮廓点 v(s)=v[x(s),y(s)],s∈(0,1)组成的轮廓参数曲线。通过构造能量函数:
使得总能量达到最小,从而得到一个好的轮廓。式中,Esnake为总能量;Einternal为内部能量,通常由曲线内部性质决定,要求曲线光滑、连续;Eexternal为外部能量,通常由图像决定,外部能量推动轮廓点达到边界;Econstraion为约束条件。
总能量的连续形式表示为:
内部能量表达式为:

和的两项离散式为:
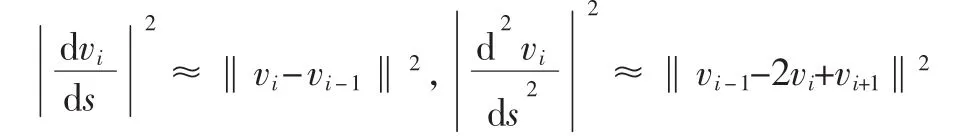
外部能量表达式为:

式中,I表示图像。
2 Williams提出Snake模型的贪婪算法
传统Snake模型求解中通常使用变分法,这种方法虽然简单,但却存在较多问题,如高阶导数的计算对噪声敏感,有可能导致结果不稳定等缺点。Amini等[4]人指出变分法的缺点并提出了动态规划算法,克服了结果不稳定的缺点,但这种算法计算量大。在此基础上Williams等[5]人提出了解决该问题的贪婪算法,使得计算量大大降低。但在贪婪算法中,能量函数和Kass等人提出的稍有不同,总能量式为:

3 模型改进
Snake模型不能收敛凹陷区域可归结为内部力在凹陷区域不够大或不够合理,需对该项进行一定的调整。通过增加新构造力实现对内部力的调整。引入新构造力不应使参数个数增加,因为这使得在算法实现时不易调整。



Econt(vi)为连续性能量即内部力所产生的能量,参考文献[6]中新构造力Ew(vi)为内部力产生的能量,以下给出Ew(vi)和Ecure(vi)之间的关系。
定理:设 vi(i=1,2,…,n)为图像轮廓初始边界点,o为初始边界点的中心,则必有:Ew(vi)=Econt(vi)。
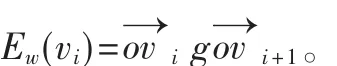

图1 锐角三角形示意图
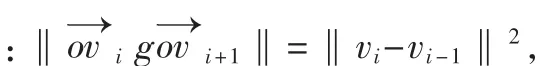

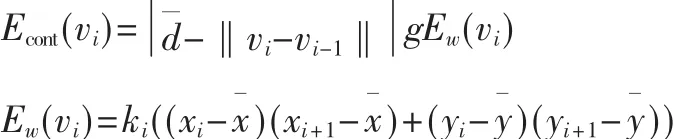
这样的修正既保证了内部力产生强大的收缩力,又保证了点迭代时各点之间的均匀性。Ew(vi)推动轮廓点向着凹陷区域收缩。这样Snake模型仍可写为:
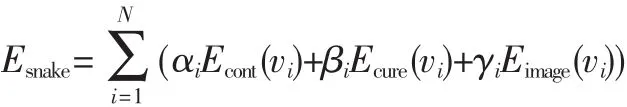
式 中 ,αi、βi、γi为 权 值 ,Ecure(vi)是 对 内 部 能 量 的 修 正 ,参 数个数不变。
4 算法的实现及结果分析
算法的实现采用贪婪算法,手工选取初始边界点,并分两阶段完成:
(1)采用改进Snake模型形式。由于传统的Snake模型中结果对初值依赖很强且容易收敛到噪声点,而Ew产生的内部收缩力可使得轮廓点迅速收缩到一个很好的范围且越过噪声点,故在该阶段采用改进Snake模型形式。这个阶段引入能量Ew起着主要作用。
(2)采用Williams的Snake模型。为了防止收缩力过大,越过边界,所以应在适当的时候减弱内部能量而采用Williams的Snake模型。采用128×128的黑白图像进行分割实验并与传统的Snake模型结果进行比较,传统Snake模型求解仍然用Williams所提出的贪婪算法实现。
两种模型分割效果如图2所示。

图2 两种模型分割效果对比示意图
两幅图像的实验效果图中采用传统的Snake模型进行分割时参数取值均为:α=1,β=1,γ=1,迭代 100 次。 在采用改进Snake模型进行分割时参数为:
图2(a)、(b)中参数分别为:α=2,β=1,γ=1,第 1 阶段迭代 10次,第 2阶段迭代 15次,共 25次。图 2(c)、(d)中参数分别为:α=3,β=1,γ=1,第 1 阶段迭代 10 次,第 2阶段迭代15次,共25次。
本文采用改进Snake模型和传统Snake模型相结合的方法并用两阶段贪婪算法实现图像分割。实验结果表明,该方法对深凹陷及更复杂区域都是有效的;分割结果受初始轮廓点影响不大、不易收敛到局部噪声点;对于各种类型图像,实现算法时参数易调整。
该模型和算法求解的改进主要解决了复杂区域分割问题,新的能量函数的引入使得初始轮廓点向边缘收缩能力大大增强且减弱了结果对初值的依赖,但在减弱分割结果对初值的依赖性方面还不够理想,如何更大程度地降低分割结果对初值的依赖仍需要进一步研究。
参考文献
[1]KASS M,WITKIN A,TERZOPOULOUSE D.Snakes:active contour model in brady IM,rosenfield a eds proceedings of the 1st international confererce on computer Vision[C].London:IEEE Computer Society Press,1987:259-268.
[2]DUNCAN JS,AYACHE N.Medicalimageanalysis:progress over two decades and the challenges ahead[J].IEEE Trans.Patt.Anal.Mach.Intel., 2000,22(1):85-106.
[3]DAVISON N E, EVIATAR H, SOMORJAI R L.Snakes simplified[J].Pattern Recognition, 2000,(33):1651-1664.
[4]王元全,汤敏.Snake模型与深度凹陷区域的分割[J].计算机研究与发展,2005,42(7):1179-1184.
[5]WILLIAMS D J,SHAH M.A fast algorithm for active contours and curvature estimation[J].CVGIP:Imag.Under.,1992,55(1):14-26.
[6]张辉,戴芳.基于 Snake模型的复杂区域图像分割[J].激光与红外,2008,38(4):404-406.

