基于融合树的事件区域检测容错算法

张书奎，王宜怀，崔志明，樊建席

(1. 苏州大学 计算机科学与技术学院，江苏 苏州 215006；2. 江苏省现代企业信息化应用支撑软件工程技术研发中心，江苏 苏州 215104)

1 引言

部署在检测区域中由大量节点组成的无线传感器网络，每个节点都具有一定的计算、感知能力以及有限的能量，目的是协作地感知、采集和处理网络覆盖区域中感兴趣事件发生的信息，并发送给观察者。某事件的发生认为是环境状态的异常改变，它可能以多种方式出现。随着时间的推移，若传感器读数保持平稳，则认为此环境对传感器检测来说是时空关联的[1]，可见，位于同一区域中邻近传感器的读数关系密切。当某时段传感器感知的读数偏离了正常值，或者邻居节点的读数大大超过了预定义的阈值，则可能是某事件发生或是传感器产生了故障[2,3]。但是，传感器节点报告错误读数的原因是多方面的(如与邻居传感器的读数不同或虽然没有超过预先设定的阈值但却与它在上一时间间隔感知读数不同等）。若发生了通信或硬件故障，这些错误会导致节点无效，意外破坏或恶意通信线路的改变也会导致无效节点的产生。环境受其他因素的影响，传感器也可能产生瞬时的错误读数。特别是部署在粗糙环境中的动态传感器网络进行感兴趣事件的检测，由于网络拓扑结构发生变化，也会导致错误读数的产生。一般来说，传感器的错误一般可分为两类[2]：一类是误判错误，即当环境处于正常状况时，传感器却报告有事件发生；另一类是失判错误，即当有特定的事件发生时，传感器却没有报告事件的发生。所以，在无线传感器网络中，保证原始数据的可信性，消除错误读数的影响，是事件区域检测需要解决的关键问题之一。

文献[4]提出了事件区域检测的一种局部分布式算法。该算法假设事件是空间相关而错误是空间不相关的，且每个传感器发生错误的概率相同。作为一种局部算法，它仅需要每个传感器与自己的邻居交换读数，从而获得邻居节点检测事件发生的统计概率，利用Bayesian分析，判定发生的是故障还是事件。文献[5]则改进了文献[4]的算法，考虑了传感器误差和错误引起的对事件判断的影响以及如何选择合适的邻居数目，达到容错的同时减少数据交换的目的。文献[4～8]都是基于概率分析的方法，而且需要传感器进行复杂的运算。文献[9]提出了一种相对简单非概率的检测算法，通过两轮投票以及少数服从多数原则，确定发生的是故障还是事件。

关于事件边界检测的研究，文献[10,11]认为，事件的边界是指事件区域与正常区域的分界线。如果一个传感器的邻居中既有异常的读数，又有正常的读数，那么就认为该传感器位于事件区域的边界。已有的事件边界检测算法依然是基于事件是空间相关的假设，同时采用概率分析的方法。还有一类工作关注于错误诊断[12]，这类工作关注的是如何确定错误发生的范围或者引发错误的错误源，而不是事件发生的范围。文献[13]介绍了一种基于簇头构建四叉树的方法进行边界检测，每片叶子与长方形区域相对应。与四叉树的聚类方法不同，本文构建了一种易扩展的二叉查询树，该查询树可以覆盖整个感兴趣的区域，能快速将事件发生的信息从感知节点传输到Sink。文献[14]是使用一种基于分类的边缘检测机制，由线性多项式描述事件边界，由此判定事件是在检测区域的里面还是外面。然而，一个线性多项式不可能获取事件发生的精确细节。而本文是通过构建多元回归模型来近似检测区域的感知值，没有洪泛而是使用融合树进行事件边界检测，以事件的时空关联特性检测整个区域，而不是通过2个事件之间的边界来判定事件的发生。

分布式核回归文献[15]与本文的算法有相似之处，但也存在着较大不同。前者，任何一个节点都含有它局部区域范围内的近似参数，因而，它不能正确回答自己局部区域之外的查询， 每个节点发送含有一个向量（向量用来描述覆盖它的局部区域）的信息，这个向量的大小随着大量的和它共享核变量的邻居节点的增加而增长，这对于资源受限的传感器节点来说，是难以忍受的。

针对目前在上述方面研究的不足，本文提出了一种基于融合树的事件区域检测容错算法，改算法分为2个阶段。首先，构建分布式融合树，每个感知节点仅报告自己的感知数据到最邻近的树节点，树节点执行多元线性回归，获得事件区域检测的估计值，传输的是描述事件区域检测的多元回归模型的系数，而不是实际的感知数据，Sink通过直接查询根节点就可获的感兴趣区域内任一位置的感知值，减少了事件区域检测的通信代价和复杂性。其次，在所构建融合树的基础上，可以对单个或多个同时发生的事件进行容错检测，识别有故障的传感器节点和发生在边界区域的事件，快速把检测读数传给基站，减少数据传输的能量消耗和延迟。

2 融合树的构建

融合树（AT, aggregation tree）的构建是事件区域检测过程的基础。其目标是减少数据传输量，提高检测精度。对数据融合算法的理论分析表明[16]，在完全融合的情况下，寻找最优融合树的问题等同于求解最小Steiner树的NP完全问题。为此，需要在计算处理能耗与传输能耗之间进行权衡。下面讨论融合树的构建过程。

2.1 网络模型

设N个资源受限的静态传感器节点随机地部署在检测区域R=(r×r)内，用集合S=(s1,s2,…,sn)描述，其中si表示第i个传感器，如图1所示。每个节点通过三角剖分[14]都有它的位置信息，节点si位置用(xi，yi)表示，且每个节点具有唯一的ID、相同的计算通信能力和能量资源。节点通过时间同步服务[15]达到宽松的时间同步，通信接入采用CSMA/CA以减小信道冲突。本文的目标是在此N个节点的网络中构建融合树，AT由Nt个节点组成，叫作树节点，树节点用于接收并融合数据，其余(N-Nt)个节点叫作非树节点(NT, not tree node)，每个NT节点感知指定区域事件属性的变化，并将感知数据传输到它最邻近的树节点。构建的AT扩展到整个网络，以便Nt个树节点均匀一致地分布在网络中，这样，可以确保检测属性值以尽可能小的跳数由NT节点传送到对应的树节点，从而延长网络的寿命。为简便起见，Pevent(在图1中矩形框里的虚线表示)代表事件，Revent表示事件区域且ReventR⊆。正常情况下，AT覆盖检测区域里所有的事件。R＇定义为R中没有被覆盖的部分，即R′= R-Revent。

图1 网络模型

2.2 树的生成

某事件的发生会触发网络中的部分节点使其读数异常，这可能是一个孤立点，也可能是多个。为确保AT扩散到整个网络，感知值由传感节点通过较小的跳数传输到相应的树节点，尽可能保持分散节点的拓扑稳定性以维持原有较好的感知覆盖范围，为此引入了Voronoi图以及相关Delaunay三角网络来描述感知网络拓扑[17]，并基于 Delaunay三角定义，构建以事件中心节点为根的感知网络融合树——伸展树。伸展树是一种二叉树，其优点在于不需要记录用于平衡树的冗余信息。设e为平面上的点，则

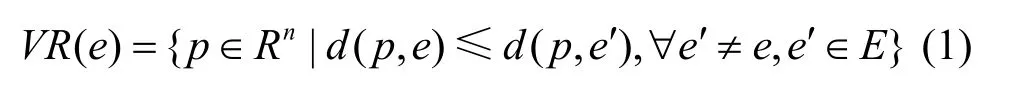
称为Voronoi多边形。则Voronoi图定义为

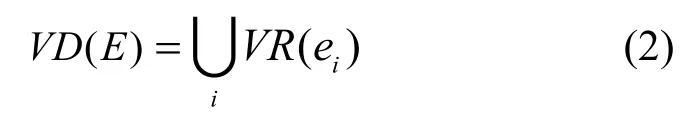
即平面上所有Voronoi多边形的集合，而Delaunay三角网络则为连接所有相邻的 V-多边形的生长中心所形成。Delaunay 三角网具有很多重要的性质[17]，通过Delaunay 表达不仅可以获得每个节点的邻节点信息，而且可以用来查找最接近的节点。基于传感器网络的 Delaunay 描述，构建以事件中心节点为根的伸展树。设目标区域为A，区域中的感知节点集为

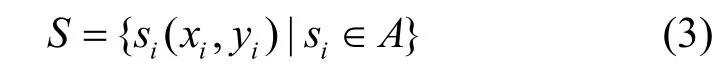
其中，(xi，yi)为节点si的位置坐标。由节点集S构成网络对应的加权无向图为G，各边所对应的权值为节点间距离。并设感知区域外存在点集K={ki(xi，yi) | ki∉A}，则目标区域中以节点si为中心相对于点集K的节点伸展树定义为T，有：

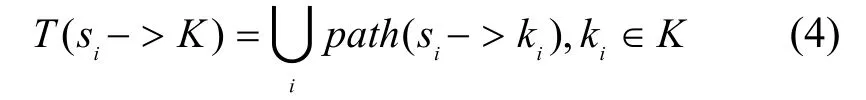
其中， p ath( si-＞ ki)为无向图G中从si到ki的节点间的最大跨度路径，其长度为l。在此路径上，各节点间的最小距离大于或等于G中任何其他从si到ki路径上节点间的最小距离。最大跨度路径反映了两节点之间具有伸展性的一条通路。需要指出的是，在一个特定的无向图G 中，两点间的最大跨度路径并不唯一，可能存在多条。而对于不同的域外节点集，相应的以根节点为中心的伸展树也并不唯一。

设树的深度为p，树节点存储感知的属性值， 这样的树被认为是平衡的，它减少了数据丢失增加了数据融合的精确性[15]。算法Form_AT是由给定的深度创建伸展树。每当一个节点要选择它的2个孩子时，就选择跨度最大的2个节点，可确保树在扩散时覆盖尽可能多的感兴趣区域，伸展树形成后，各子区域中所有剩余节点向距离自己最近的树节点发送数据。本文通过3种消息即Beacon、Probe和Join实现树的构建。图2描述了消息交换构建融合树的过程。

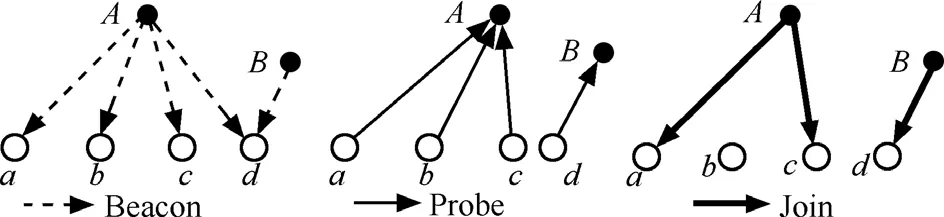
图2 消息交换构建融合树

1) Beacon消息。

在d-跳邻居发现过程中每个节点u在d-跳范围内广播Beacon消息NMu={Message，u，Hop}，其中 Message为消息类型， u为节点 ID，Hop字段为消息跳数计数，初始为0，接收到NMu的节点v将u加入自己的d-跳邻居列表对接收到的一份或多份冗余 NMu，v选择 Hop值最小的NMu， 将其Hop字段加1并更新Hopu,v=Hop，如果Hop＜d则继续向邻居广播，然后v进入等待状态。如果v在等待状态时又侦听到Hop+1＜Hopu,v的NMu，则记录该消息并将Hop字段加1重复上述过程；否则v不作任何动作直到计时器超时。这里计时器时长可以设为网络初始化阶段时长。

对于来自不同节点的Beacon消息，接收节点v都执行相同的过程。图3是Beacon消息处理过程的自动机表示。通过Beacon消息广播每个节点v可以获得 d-跳范围内节点集合，Hopu,v表示由这种带跳数更新的广播重传过程所得到的节点u，v之间的近似最短路径跳数。由于传感器网络静态部署，对每个节点u，是稳定的。这里即为所有可能树节点成员的集合。在 j层的每一个节点向它所有的下一跳邻居广播一个Beacon包，这样，j+1层的节点从j层接收到多个Beacon包，从中随机选取一个概率值p′ ＞ p′的节点作为它们的父节点，并向它发送一个Probe包。

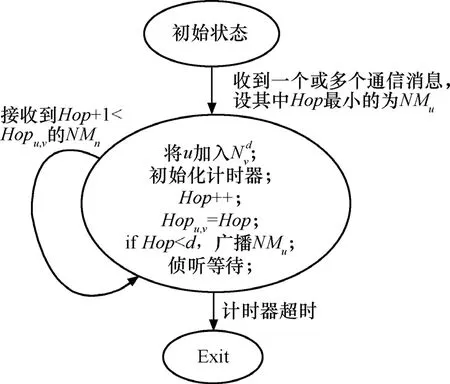
图3 节点的Beacon通知消息处理过程

从图2可以看出，节点d从A和B接收Beacon，p′（该算法的一个输入）的值按如下方法优化。

设父节点i以通信半径 r，向圆心角为120°的扇形区域广播它的 Beacon消息，该扇形区的面积为

这个区域的节点数为

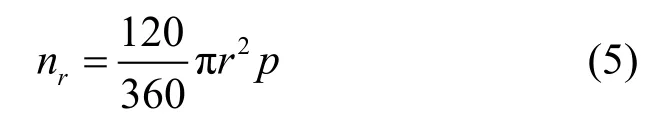
其中，p为树的深度。按如下的二项式分布，选择区域内概率为p′的2个节点作为它们的父节点。

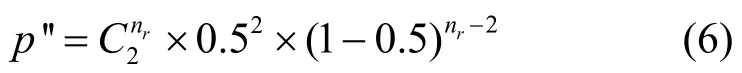
如果一个节点从预期的父节点那里接收到了多个Beacon消息，那么它们的ID将会被新选择的父节点所保存，以便于在节点失败的情况下快速恢复。

2) Probe消息。

选定的父节点等待从它的孩子节点处接收Probe分组，之后，决定选择哪2个作为它的孩子节点。一旦它收到了它的下一跳j+1层所有节点的消息，就会选择离它最远的2个节点作为它的孩子。那些没有被任何父节点所选择的节点将不再尝试成为AT的成员而转化为感知节点，这样，树(因为传感通信的代价远大于存储的代价)的大小能适当减小。从图2可以看出，节点d选择B作为它的父节点，并向它发送一个Probe分组，而后，节点A向节点a、b、c和d发送Beacon消息但是仅从节点a、b和c接收到Probe分组。

3) Join 消息

父节点在选择了孩子之后，向它们发送一个Join消息，宣布将它们加入该树。从图2可以看出，A选择节点a和c作为它们的孩子，而a和c距离A比a和b或者b和c都远。

融合树构建算法Form_AT(p，p")描述如下。

输入：树的深度p和父节点选择概率。

输出：深度为p的二叉树Tc且每一个节点分配唯一的ID

1) 对于第j层，深度从0到p-1的每一个节点i从 1到2j；

2) Mi是j +1层的一个节点；

3) ni是在j层上的一个节点；

4) 在Mi的通信范围内的节点ni(Mi＜ r),发送包含其ID 的Beacon包到Mi；/* r为通信半径 */

5) 对于大于p"且跨越路径长度最大的节点ni,Mi选择它作为其父节点；

6) Mi发送 Probe 包到 ni；

7) ni等待 NWAIT 时刻(恰当的时间周期)从选择ni作为父节点的Mi接受Probe包。

对于传感器网络来说，在最大跨度路径上的节点具有较好的分散性，减少了由于覆盖重叠而对网络感知能力所造成的影响，因此这些分散性好的节点需要保持。通过节点伸展树的定义，确定了传感器网络中需要保持的节点集。基于此节点集，对于覆盖重叠节点也可有效地提高网络整体的感知能力。

2.3 数据融合

基于伸展树的数据融合算法的主要思想是采用传输能够拟合较多的检测数据的模型 M 来代替传输节点的检测数据，其目的是为了减少数据传输量，从而节省传感器节点的能量。因此需要考虑回传以参数表示的模型的代价和其可拟合的数据量之间的关系。传输模型的代价越小其能够表示的数据越多，节点就越节省能量。由于节点检测值往往要受多个因素的影响，期望用最小代价模型拟合最多的数据，且计算简单，而多元线性回归模型恰好符合这一目标。

融合树中的每个节点接收并存储由最近的非树节点周期性报告给它的数据，即NT节点负责感知而AT节点负责存储，将存储在AT节点里的值看作是输入x-y坐标的函数值，此过程由三元组(f，x，y)描述，这里 f为位于(x，y)处节点的感知估计值，由AT中存储在节点i的数据及其子节点发送的多元回归模型的系数执行多元线性函数回归生成。下面讨论这种数据融合过程。

设多元线性回归模型形式如下[18]：

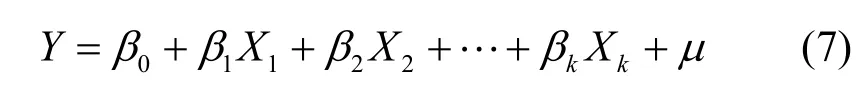
其中，Y为感知估计值，Xj(j=1, 2, …，k)为对感知估计值Y发生作用的影响因子，βj(j=0, 1, 2, …, k)为k+1个未知回归参数，μ为随机误差项。由于参数βj(j=0, 1, 2, …, k)都是未知的，可以利用样本观测值(x1i, x2i, …, xki；Yi)对它们进行估计，由此得到的参数估计值为用参数估计值替代回归模型的未知参数βj(j=0, 1, 2,…, k)，则得到多元线性样本回归方程为

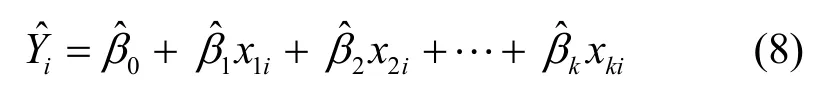
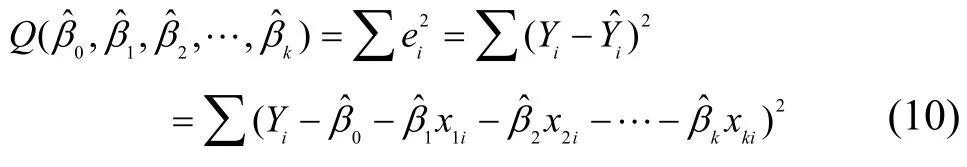
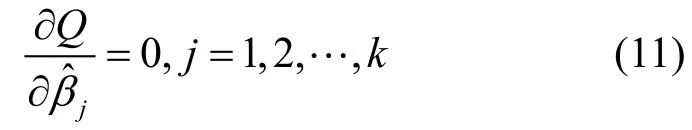
将上述k+1个方程化简得下列方程组：

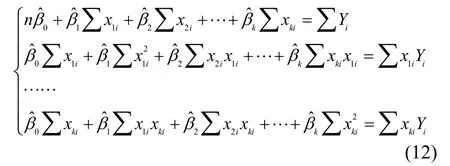
其矩阵形式为

经化简得如下方程：

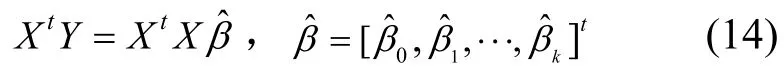
设R(X)=K+1， XtX为(K+1)阶方阵，则 XtX满秩，其逆矩阵存在，所以β的最小二乘估计向量为

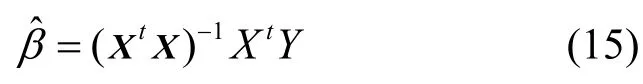
运用多项式回归，得到如下方程：

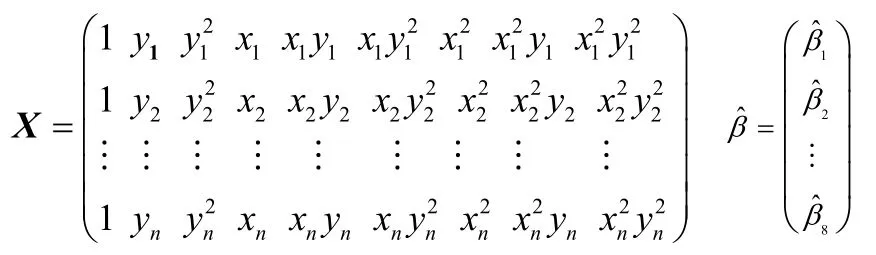
其中，

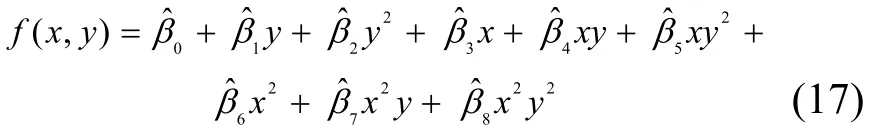
数据融合算法SPAT(p, ns)描述如下：/* ns为感知节点向树节点报告的平均数*/

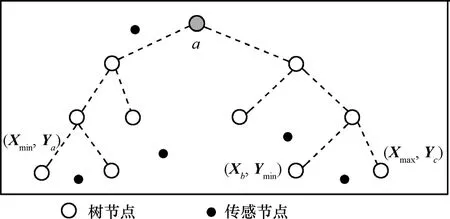
图4 融合过程中边界区域的计算

1) 对于树中的每一个叶节点i

其节点的数据被读取；

执行多元线性回归，其系数 β0，β1,…,β8被存储；

2) 初始树的深度为2p

While 当 p ＞0 时

sum = level + 2p-1

k = level

while k ＜ sum

3) 对于树中的每个非叶节点 k，在(xmin, ymin)和(xmax, ymax)的范围内计算其位置x-y点报告给它的2个孩子节点i 和i+l；

4) 计算新的(βi0, βi1,…,βi8)和(β(i+1)0,β(i+1)1,…,β(i+1)8) ,添加到节点k的信息中，然后调用回归函数计算(βk0,…,βk8) ,传输到它的父节点；

5) 转到下一级深度继续。

相对于传输原始数据到 Sink节点的能量消耗和时延，通过SPAT融合过程报告数据更为有效。在AT中，设压缩比定义为将原始数据压缩之后再传送的字节数与原始数据之比。设深度为 p的AT共有 t = 2(p+1)- 1个树节点，每个大小为wi字节的数据分组包含感知读数和该读数所对应的位置坐标。这样，输入到每个叶子节点的字节数大小为nswi，其中ns为感知节点向树节点报告的平均数。所以，传输到叶节点的字节数

除了从感知节点读取检测值以外，每个非叶节点用从它的2个孩子那里得到值作为输入来更新系数和区域边界的x-y值。所以，输入到非叶子节点的字节总数Tnl为

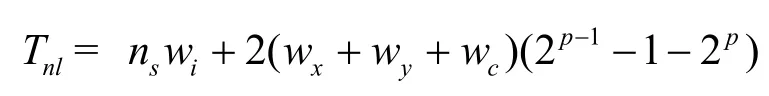
从树节点获得大小为(wx+ wy+ wc)字节的输出分组(包括系数和x-y的范围)。

从所有节点输出的字节总数 T0= ( wx+ wy+wc)× (2p-1- 1 )s，那么压缩比为

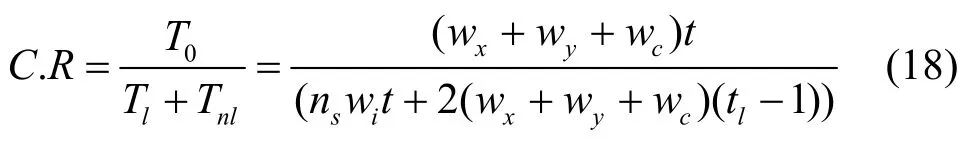
其中，t为树节点总数，lt为叶子节点数。

3 事件区域检测

在许多应用中，使用函数 σ (i, t)=F (v1, v2,…,vk)来描述检测区域的状态信息(如温度，湿气等)，这些信息由感知传感器 i∈N在时刻 t获得，其中 vk是影响传感器读数的参数。一般来说，由于已知或未知因素的影响，很难得到准确的函数表达形式。除一些特例外，时间变化以及线性或非线性的其他因素也可能会影响检测读数，而这些因素很难形式化表示。例如，一个温度传感器的读数受很多因素的影响，如地点、天气、时间等。本文不是设法得到一个确切的函数表示，而是形式化函数F的基本属性，从而分析传感器的读数σ(i,t) 。

3.1 事件区域检测的性质

设传感器节点对某一区域的检测读数，有以下性质：

1) 每个传感器节点是独立的；

2) 存在 2个常量 Cmin和 Cmax(Cmin≤σ(i, t)≤ Cmax)，分别是传感器检测获得读数的最小和最大值；

3) 在[Cmin, Cmax]内，σ(i, t)连续且服从密度函数为φ(i)的正态分布，期望值为

性质 1）说明传感器独立地检测环境变化，性质 2）说明正常传感器读数的变化范围，性质 3）说明，传感器检测读数的变化空间，由适合正态分布的应用事例确定，如每日气温、风速等。本文对正常与错误读数的判定条件如下。

正常读数：通常情况下，检测读数σ(i, t)在[Cmin,Cmax]内且服从正态分布φ(i)，若存在τ1＞0，使得检测读数满足 |σ (i, t) - E (i )|≥τ1，说明传感器读数超出了正常范围。满足该条件的节点越多，事件发生的可能性就越大。

错误读数：对于传感器i，φ(i)满足以下3个条件中的任一个，该传感器可能为故障传感器，其检测产生的读数为错误读数。

1) 若存在τ1，τth且τth＞τ1＞0，对于∀ t, | σ(i, t)-E(i)|≥τth，说明传感器的读数超出了正常范围，它很可能是有故障的。如果传感器频繁或者持续报告这样的读数，那么认为这个传感器是有故障的。

2) 在事件报告的几个连续时期，有|σ(i,( t+1)-σ( i, t )|≈ 0 ，若存在常数c，使得节点i的邻居传感器 i′满足|σ(i′,(t+1 ) - σ (i′, t )|＞c，即邻居传感器 i′读数随着时间的推移发生变化，而传感器i的读数却是恒定的，那么传感器i是有故障的。同理，在一个特定的阶段，有|σ(i',(t+1 )-σ (i', t )|≈ 0 ，如果一个传感器 i的邻居传感器 i'检测到一个很小的读数变化，传感器i的读数却有很大的变化，那么这个传感器i是有故障的。

3) ∀t ,Cmin＜ σ (i, t) ＜ Cmax, σ( i,t+1) ＞ τ2,Cmin＜σ( i, t + 2 )＜Cmax, σ(i, t + 3 ) ＞τ2,这个条件表明传感器的读数呈不规则变化，那么传感器i是有故障的。例如，传感器的读数周期性地或间歇地从正常读数变化到事件读数，再变化到正常读数。

为提高检测读数的准确性，首先要识别有故障的传感器。由性质1)可知，通过对当前读数σ(i, t)与期望值E(i)进行比较判定i是否发生了故障，设树节点的数量 nt总是满足条件 nt≫ 3 nnmax+1，其中ntmax表示故障树节点的最大数量，该条件确保有故障的传感器能被有效识别[10]。另一方面，为增加有故障节点事件检测的置信度，每隔一个时间间隔，对可疑传感器是否为故障点进行判断，一旦检测到故障节点，立即隔离。设ri是函数σ(i, t)的一个实例，这里σ(i, t)表示在一个特定时刻传感器的读数(如温度、声音，氧气密度等)。在没有错误的检测数据时，事件定义为传感器的异常读数，有如下定理。

定理 1 当事件发生时，存在σ＞ 0，使|ri- E (rr) |＞ σ 。

证明 (反证法)如果|ri- E (rr)|= 0，那么传感器的读数与期望值相同。这表明在没有事件发生的时，ri不变，这与事件的定义矛盾。

为了使树节点获取它周围NT节点读数的特征值，定义di作为树节点在时刻t从它周围的NT节点获得读数的平均值。由性质 1）知，每个传感器的读数不依赖于其他节点，由性质 3）知传感器读数服从正态分布，如事件没有发生，检测读数di仍然服从正态分布 φ ( di)，这样， φ ( di)的期望值其中是向树节点发送报告的平均数。

定理2 当事件发生时，存在τ1≥0，有|di-E(di)|≥τ1，且随着τ1的增加，事件发生的概率也增加。

证明 根据正态分布，当|ri- E (ri)|=0时，事件ri发生的概率很低，当φ(i)远离E(ri)时ri发生的概率很高。有 ns个传感器时，有这样，当τ1= 0时，事件发生的概率最低，且随τ1的增加而增加。

从理论上说，通过概率分布函数(φ(i)或φ( di))，可以计算期望值。然而，在现实世界中，一个传感器事先获知参数φ(i)或φ( di)是不现实的。当没有事件发生时，读数di在一定范围之内是随机分布的。所以，di可以从随机选择事例的读数中抽样。从抽样读数集合中计算渐进的 E(di)，E(di) =(d1+d2+…+dn)/N，其中N是历史数据样本的大小。这样，将错误读数的条件1)也可改为 |σ (i, t) - E (di)|＞τ2，在条件2)，用di替换σ(i, t)。通过比较当前读数di与期望数据 E(di)检测事件的发生。注意到，在|di-E(di)|＞τ1且τ1＞0的情况下，即使没有事件发生，| di- E (di)|＞ τ1也可以被满足，但不能说明某事件已经发生。然而，如定理2所述，如果增加τ1的值，以该值为阈值，事件发生的概率增加到接近100%。

3.2 单事件检测

当一个叶节点从它周围的 NT节点接收读数时，依赖于thτ是否超界来计算事件的多元回归方程fevent或正常现象的多元回归方程f。当一个父节点从它的孩子节点处接收读数时，同时也从它自己的NT节点周围采集数据并确定在它的区域范围内是否有事件发生。多项式可以是fevent或f，取决于父节点是否位于该事件区域，如果父节点同它的孩子节点位于同一区域，那么它将更新孩子节点的数据，并用它自己的接收数据计算一个新的多项式；如果父节点和相应的孩子节点处于不同的事件区域，那么孩子节点的数据不改变。这个过程一直继续，直到根节点接收到2个多项式和相对应的范围信息。按照从孩子节点接收的fevent和相对应的范围，根节点就可以根据事件位置信息估计事件的边界及Pevent的覆盖范围。

图1显示了通过融合树 AT检测 Pevent的一部分，Pevent发生在Revent的内部，在R的一个角落，父节点A和它的2个孩子节点B与C所在子树位于Revent事件区域内，此时，B和C从NT节点那里接收到的读数其偏差远大于τth(即|di- E ( di)|＞ τth)。另外，B的孩子节点也在Revent中。因此，B节点从它的2个孩子节点处接收到了回归方程的系数。因为B节点本身也从最近的NT节点接收到了偏差远大于边界的数据，所以它产生了一个自己的报告和更新数据后的新fevent，然后把新的fevent和相应的范围值传给它的父节点A。在父节点为C的子树中，其中一个孩子D在Revent中，而另一个孩子E却在R中。C接收多项式 fevent(从节点 D)、f(从节点 E)及相应的坐标范围{xdmin，ydmin，xdmax，ydmax}和{xemin，yemin，xemax，yemax}。通过观察由它本身和它的2个孩子传送数据的近似区域，C得出这样一个结论：D和它位于同一个区域内。因此，D节点更新数据再结合它自己的检测数据产生一个新的fevent，然后C把fevent及D的坐标范围、未变化的f及E的坐标范围传送给A。这样当它沿着AT映射到Revent中包含多个树节点的区域时，这些范围不断被更新。当根节点接收一个子节点处的范围和fevent，根据事件Pevent和它的域范围得到一个估计值。

3.3 多事件检测

相对单事件而言，多事件发生时树节点之间交换的数据分组、计算复杂性都将提高，随着事件源的增加，每个事件影响程度却会减小[17]。考虑到这种现象，本文设计的检测方法其基本思路如下：当数据分组被传输到树节点时，如果其中一个子节点有与父节点相同或相近的数据集，则结合2个数据集形成一个新的多项式；如果没有子节点同父节点相同的数据集，则通过数据变换以及范围变换来构建融合树；如果2个子节点数值接近，则合并它们的检测范围得到一个更大的区域。

设在某矩形区域里，存在2个异常事件和一种正常现象。如图5所示，在区域R里发生了2个事件 Pevent1和Pevent2。B检测事件Pevent2，而它的孩子节点C和D分别检测Pevent1和一种正常现象，在这种情况下，C和D把它们各自的多项式与坐标范围{xcmin，ycmin，ycmax}以及{xdmin，ydmin，xdmax，ydmax}一起传输到B。B计算2个节点接收数据的最小值和最大值，得到它们的数据范围。B将Scmax，Scmin，(Scmin，Scmax分别表示最小和最大的事件属性值)C的坐标范围以及 Sdmin，Sdmax，D的坐标范围一起变换到 A。如果使用单一事件检测方法，则需要6个数据分组，其中3个与3个多项式相对应，另外3个与3个区域范围对应。此外，A的其他孩子节点G和D的读数比较接近，所以，A把它们的范围结合在一起，感知同一个事件Pevent2。然后，A创建新的多项式，将它的系数、区域范围和事件属性的最大最小值传输到它的父节点H，M的估计值同A发送的也一样，结合N产生的数据之后，发送它的系数到根。由于H和I在R内，H没有修改Pevent2事件的区域范围且不加修改地传送到根，由此确定了事件区域及其边界。这样，事件Pevent1和Pevent2都通过有限的计算检测到了，且每棵树仅执行了一次多项式回归。

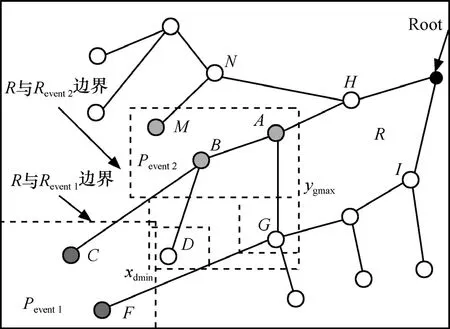
图5 2个事件发生的检测

3.4 故障节点检测及错误读数的控制

前面讨论了基于融合树方法完成事件区域检测过程。但是，这个过程忽略了某些隐藏在事件区域内的故障传感器产生的错误读数。由于传感器的读数在计算最后的多项式fevent时被树节点结合成一体并代表事件的特征，错误读数必定影响这个结果的准确性。这一部分，分析在网络模型里如何检测故障传感器节点。

由融合树的构造过程可以看出，R中的AT分布广泛，以至于从网络的所有角落都能够接收数据，这样可确保更好的空间逼近，因为树中的每个节点选择2个离它最远的节点作为孩子，对密度较大的网络而言，如果NT节点是有故障的，将向最近的树节点报告错误读数。从文献[6]获知，除非传感器位于事件的边界，否则节点k的邻居节点的读数与节点k的读数近似。图6描述了故障传感器的检测过程，圆形表示节点的传感区域，此方法可以被扩展到检测多个故障点。

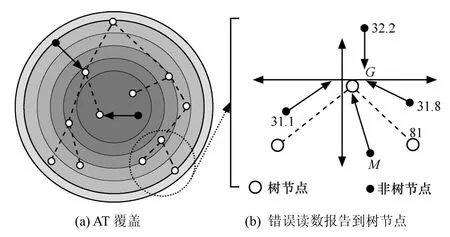
图6 故障节点的检测与报告

设M是有故障的NT节点，将读数传输到离它最近的树节点G，如图6(b)所示。M四周的传感节点正在传送正确的温度，节点M的异常读数81，此时|σ(i, t) - E(di)|＞τth。由于M 4个方向的邻节点传送正确的可接受的读数(除了M)，因此M被看成是有故障的节点。如果M在接下来的几次连续报告读数，满足|σ(i, t) - E(di)|＞τth时，它将被禁止传输数据。因此，为了预防错误数据影响最终多项式构建，M发出的读数将在检测进程中被剔除。

需要说明的是，树节点本身不能做出正确的判定，判定是通过每一个树节点传播它的位置(x, y)及其函数值f(x,y)到AT中的其他节点经计算形成的。为保证传输信息量可控，按以下步骤交换故障 NT节点信息。

1) 从Sink开始，以Sink为中心，fevent被发送到所有的树节点，最坏情况下需要(nt-1)次的数据分组传送。

2) 对当前的树节点j，接收M发送的数据并且验证M是否是故障节点，正向路径转发(x, y)和f(x,y)到所有j在树中的邻节点。

3) 当收到这样一个数据分组时，节点i首先转发该数据分组到它的邻节点，发送分组的节点除外。接着，节点i更新M在4个方向上的邻节点位置，并且使用它们的多项式重新生成在这些位置上的数据值。使用这些数据值，通过检查是否满足判定错误读数的3个条件之一，i作出M是有故障的还是正常的判断。当M落在2个事件区域边界时，存在2种不同的读数，虽然正常但还是被拒绝。

4) 相对以前的正向路径，以反方向通过节点i传播M是故障节点或是正常节点的消息。每一个节点接收到M的消息后，作为主要依据更新自身的判定。然后，它再一次以反方向转发它的判定，最后，节点j作出拒绝或接受M节点读数的决定。

如图1所示，一个故障NT节点M发送它的读数到它最邻近的节点N，N认为M是有故障的，则发送它的位置和读数f(x，y)到它所有的邻居节点。每一个邻居节点收到消息后，产生一些与M近似的位置信息，同时通过它的多项式产生在这些位置的读数。然后，把M的f(x，y)值与这些新产生的值比较，检查是否满足传感器故障判定条件。接下来，它向在相反路径中的所有节点广播它的检测报告，每一个树节点接收它的邻居节点发送的读数，在收到大多数判定的基础上，M被归类为有故障的还是正常的。最后，在大多数来自邻接树节点读数的基础上，N作出关于M为故障节点的正确判定。

4 影响性能的因素

1) 构建AT的影响。

当增加融合树AT的深度时，执行回归次数增加，多项式可能偏离原始数据更多。为了避免这些影响，AT的孩子节点数量可进一步增加，而不增加树的深度，使得AT度高而深度小。然而，由于孩子节点数量的增加也使每个父节点的计算时间增加，因此，事件检测应该在AT的基础上进行，这样可在精确度和计算延迟之间达到平衡。由于每个树节点融合了传感器的读数，计算开销是O(n/nt)，这里，nt是树节点的数量，如果nt与n同步增长，计算的开销就可以保持不变[17～19]。

2) 多项式次数的影响。

多项式的次数对获得的事件的边界和区域信息有一定的影响。在某区域内，如果大量的传感器(≫20)向单一树节点发送报告，就需要一个三次多项式来提高事件边界的精确度。三次多项式将会有27个系数。具有27个系数的三次多项式与二次多项式的9个系数比较[18]，增大了树节点向其父节点发送的数据分组的大小。然而，与大量的传感器读数相比较，27个系数是非常少的，因为传感器读数都被融合到若干系数中了。

3) 故障传感器的影响。

在第4节用τ2表示故障传感器检测的阈值。如果错误的读数没有使|di-E(di)|超过τ2的定义值，树节点就不会报告任何错误读数，隐藏了故障传感器的存在，将影响事件检测的准确性。

4)τth的影响。

在事件区域检测中，为事件检测寻找一个合适的阈值是重要的。根据定理2，即使没有事件发生，τth较小会导致频繁的发送事件报告。相反，τth较大可能忽略事件的发生。在设置τth时应该考虑2个因素，一是正态分布密度函数 φ ( di)，一是树节点样本的大小nt。如第3节所述，σ(i, t)的最大和最小分别为Cmax和Cmin，树节点从它周围的传感器收集数据时，di的最大值和最小值分别用 Cm′in和Cm′ax表示，没有事件发生时，依照φ ( di)，di在限定范围内服从正态分布，有 E(di)- Cm′in= Cm′ax-E(di)。设τth=E(di)-Cm′in。对任何给定的di，如果di＞τth，并且在nt个传感器之中至少有一个传感器是在边界范围之外，排除了故障传感器，可以说事件发生了。

5 仿真实验与讨论

本文采用离散事件仿真平台 NS2进行模拟实验，通信接入采用CSMA/CA协议，选择温度属性评估所提出方案的有效性，表1定义了所使用的参变量。设区域 A中节点总数为 D，则节点密度ρ=D/A，As是包含单一融合树Tc的子区域，因此在子区域里节点的平均数U由As确定，对于二叉树，节点总数为 t = 2(p+1)- 1 。

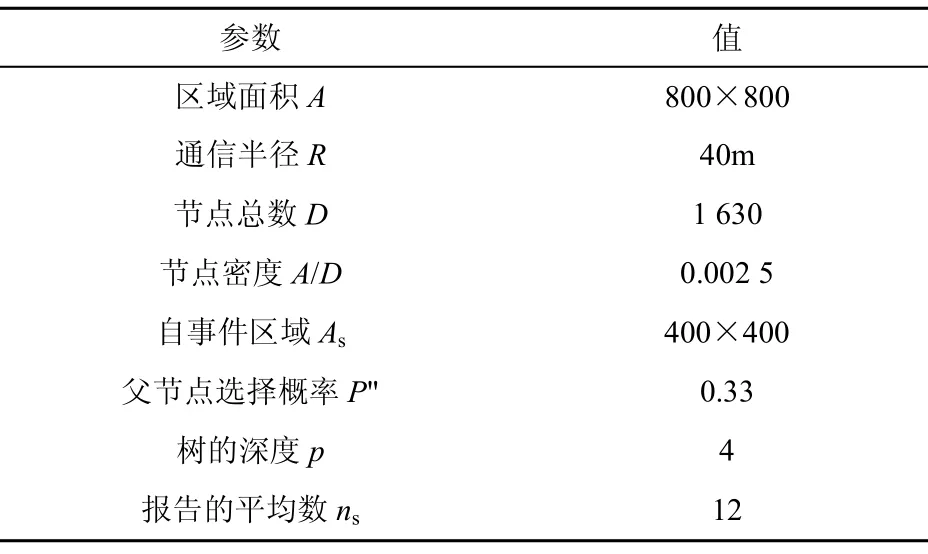
表1 仿真实验参数设置

此外，ns由前面设定，即感知节点向树节点报告的平均数，子区域里节点数U的上界为[15]

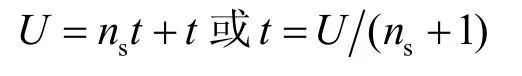
利用式(1)替换t，得AT深度的一个最优解：

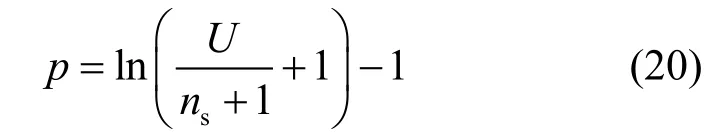
设 D=1 630，A=800×800。有 ρ =1630/8002=0.0025,As= 4 00 × 4 00，则该区域内节点平均数为：U=0.002 469×400＋400=408。设树的深度p=4，则节点数 Tc=t=2(4+1)-1=31，ns=12。此区域传感节点总数=31×12=372。事实上，该区域内的节点总数 U=31+372=403＜408。因此，上面所定义的参数是有效的。

5.1 性能评估测度

在800×800平方单元区域R内，随机部署250个节点，温度变化 30℃～35℃是正常现象，温度变化在 39℃～49℃时为异常，可能是该区域发生了火灾。树的深度设置为 4。在无事件发生时，检测的温度值服从正态分布φ(i)。Cmin、Cmax和E(i)分别为30、35和32.5，φ(i)的变化是1.2。单个事件Pevernt1在中心发生，事件区域称为Revent，E(di)- Cmin= Cmax-E(di)=2.5，τ1为2.5，E(σ( i, t) ) - Cmin= Cmax-E(σ(i,t))=2.5且τ2=τth=4.5。当事件发生时，读取的数据通过NT节点传输到最近的树节点，通过10轮实验评估以下性能指标。前提是假设查询已经广播到融合树的所有叶节点。

1) 压缩比(compress ratio)。2) 根节点输出数据分组的大小。3) 事件边界(event boundary)：将实际事件边界(不同的形状)和检测到的事件边界进行比较。4) 错误率(percentage error)：AT中根节点获得的读数与实际传感器读数的近似程度。由事件区域检测的读数与实际读数产生的偏差E表示，其中εth=10%是指定的错误阈值，nb是在边界传感器的数量，为近似读数，z为实际读数。5) 事件识别延迟(event recognition delay)：事件发生的时间与在根节点计算的近似时间之间的间隔。6)通信代价(communication cost)：事件区域检测传输数据分组的平均数。7) 故障点识别延迟(faulty sensor recognition delay)：从故障节点发送读数到错误读数在融合过程中被消除的时间，通过平均延迟和故障传感器的百分率之比表示。8) 包负载(packet overhead)：检测到故障节点时，树节点向邻近节点发送数据分组的总数。9) 读数误差(variance of sensor reading)：通过NT节点集（包括故障节点）报告的数据di与它们的平均值E(di)的差异来评估。10) 故障传感器检测命中率(faulty sensor detection hit ratio)：设nft表示网络中发送数据到树节点的故障传感器数，nf表示网络中故障传感器的实际数目，检测命中率为

5.2 仿真结果与讨论

5.2.1 压缩比

图 7显示了压缩比随着树的深度而变化的情况，正如所期望的那样，几乎为常量0.02。曲线的下降说明随着深度的增加，压缩比减小，树的深度越深，压缩程度越好，而且输出量大大减少。高压缩比减小了整体的信息量，因而节省了通信带宽和总的能量。

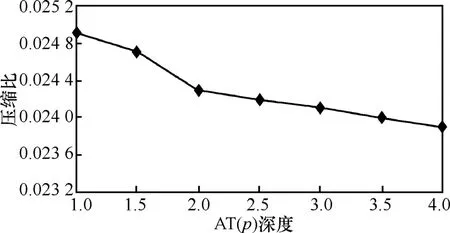
图7 压缩比与树深度的关系

5.2.2 根节点输出数据分组的大小

图8显示了在根节点处通过SPAT算法进行数据融合之后的数据通信量以及根节点收到未融合数据而进行正常的一对多通信的情况。尽管树的深度不同，但当融合树中所有节点执行数据压缩时，数据分组通过根节点传送到 Sink的大小是恒定不变的，即固定(wx+wy+wc)个字节。从一个树节点到另一个树节点所传送的数据分组大小几乎是恒定的，且与网络规模的大小无关，使得数据传输的总能量维持在合理的范围。这印证了上面的假设，即每个树节点传送的数据分组仅包含系数和x-y坐标值到它的父节点，数据分组的大小独立于树中节点的数目。而传统的多对一通信，所有的叶子节点都要向根节点发送数据，所以，当网络节点增加时，通过根节点传送的数据分组大小的增长不受限制。通过本算法执行数据压缩时，与文献[8]相比较，最大数据通信量减少85%。

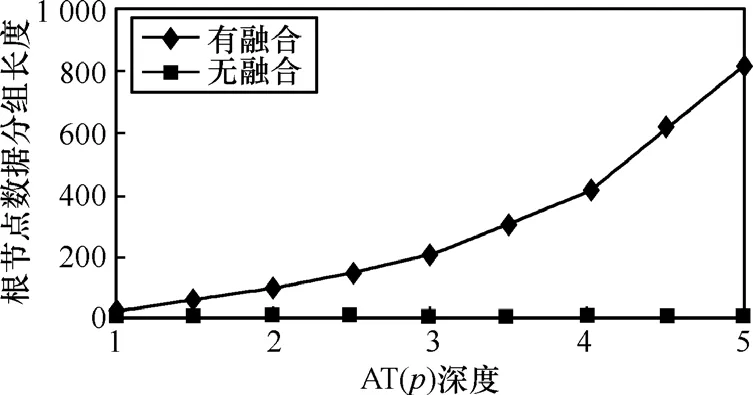
图8 数据融合与未融合的通信量对比

5.2.3 边界检测

当具有不同边界的多事件同时发生时，为了讨论基于融合树的事件区域检测性能，在R的角落里5℃～10℃变化范围内引入第二个事件 Pevent2，图 9所示。边界检测由虚边矩形描述，图中的黑色小圆点表示融合树的树节点。实验结果表明，Pevent1与Pevent2的错误率分别为7.8%和8.5%。可以看出，通过检测计算的事件区域（即虚边矩形）与实际事件区域（即粗边矩形和粗边椭圆）是匹配的，这证实ATERD是有效的。然而，由于ATERD得出的事件区域总是一个矩形（由于事件区域是利用无数个小矩形迭代构建而成），若事件自身就是矩形的，其近似效果要比利用其他形状（如椭圆）更接近原型。

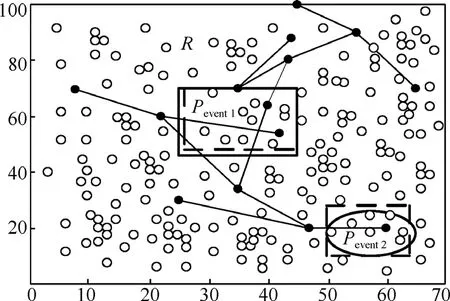
图9 ATERD检测的事件边界

5.2.4 错误率

图 10显示了融合树的深度与错误率的关系。可以看出，随着融合树深度的增加，树节点覆盖的范围会更大，从而使得整个区域能被更好地感知检测，同时近似数据的平均误差及错误率也稳步下降，这正是所期望的。树深度为1时，错误率达到最大值，是由于这棵树仅有3个节点（区域内的大多数传感节点被分散，不在树节点的感知范围内，因此无法向AT传送）检测该区域范围。图11显示树的深度为4时，错误率渐进增大达到最大值5.64。选取381个读数，发现最初部分集中了接近估值的最大数目点。当树的深度为4时，错误率最大值为5.64%，大部分节点都有它们各自的误差但限于一个较小的范围0%～1.68%。

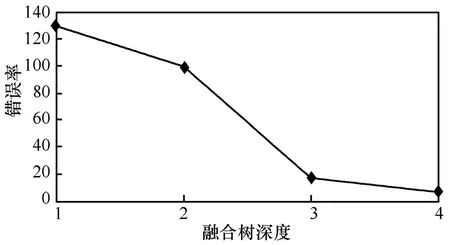
图10 错误率与树深度的关系

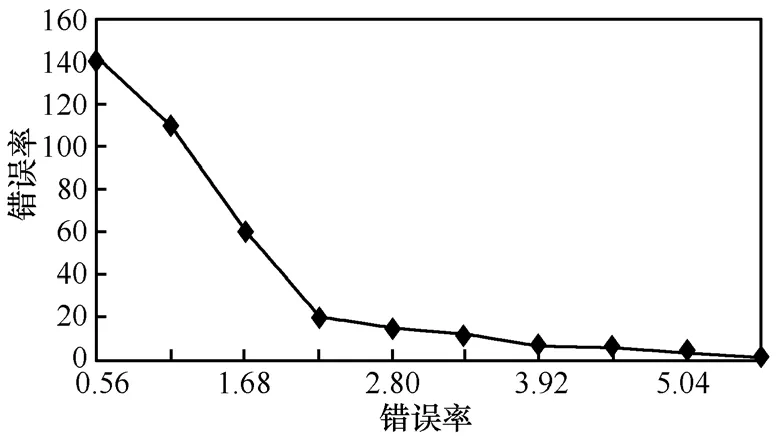
图11 树的深度为4时的错误率

当通信范围变化时，对ATERD完成事件检测的准确性进行分析，如图12所示，两事件ATERD的误差率不足10%，采用多事件ATERD进行事件检测（误差范围为6.8～8.9）比单ATERD 进行事件检测(误差范围为 6.4～7.6)高出 6%，单事件检测出现较小的误差范围，是由于近似边界可以通过最后生成的fevent较好定位，而在多事件ATERD方法中是无法实现的。由图 12可以看出，被检测事件的错误级别随通信范围的增长呈不显著变化，而文献[11]中，随着通信范围的增加，在区域Reven里有更多的传感器读数被传送到树，错误级别却随通信范围的增长急剧增加，在ATERD中，不同的读数与不同的事件相对应，树节点会生成不同的多项式，总体误差率是独立于各个传感器的通信范围的。从图12还可以看出，随着NT节点的增加，错误率缓慢增加，树节点、NT节点位于事件边界的可能性也会增加，回归多项式的准确性也会增加，进而覆盖到相对大的范围和提供更加准确的传感参数，错误率被控制在一个合适的范围内。

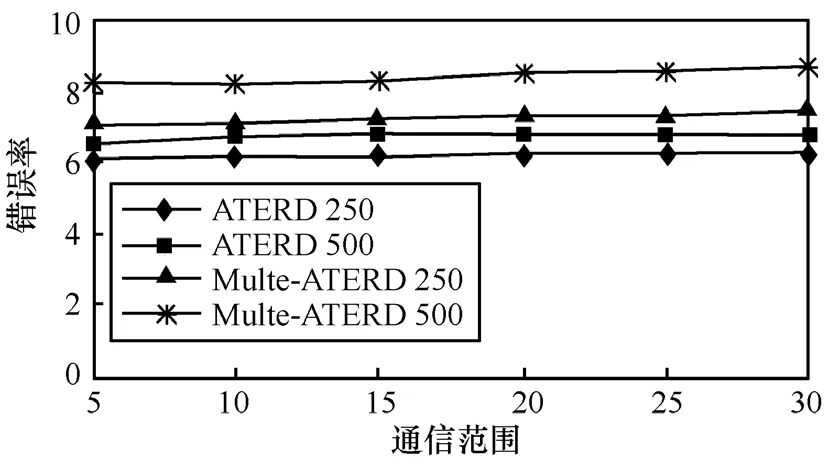
图12 通信范围、节点密度与错误率的关系

5.2.5 检测延迟

图 13表明，事件检测延迟随节点密度的增加几乎保持不变。导致事件检测延迟的主要因素有 3个方面：事件识别延迟、多项式计算延迟和事件报告的传输延迟（称为通信延迟）。从图13可以看出，事件识别和多项式计算延迟远远小于通信延迟，通信延迟占总延迟的近77%。一旦融合树确定，用于通信的延迟保持恒定并且独立于NT节点的密度。当节点密度增加，围绕每棵树的NT节点数目也随之增加。实验结果表明，当节点数目 nnt增加时，事件识别、计算负载和多项式构造也维持恒定，这是由于节点数目的增加对 ns的影响不大。ATERD之所以能够降低事件识别和事件报告的复杂度是由基于以下原因：首先，在ATERD中，事件识别和基于多项式的数据融合不含有任何复杂计算；其次，基于树的网络结构对事件识别进行了局部处理；再者，当网络规模增加时，树节点的数目也相应增加，因此ATERD是可扩展的。

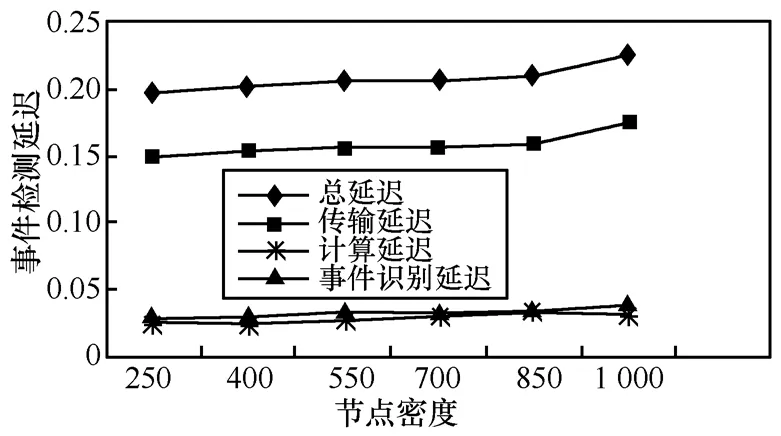
图13 事件检测、节点密度对延迟的影响

5.2.6 识别延迟

从图 14可以看出，随着故障传感器所占百分比的增加，检测时延也会缓慢增加。尽管由于密度的加大，传递给每个树节点的NT节点数会增多，但是检测故障传感器所花费的计算时长却是一个常量，同时增加的时延与每个树节点之间传递数据的传输时延相比是可以忽略的，从下面的关系式可以明显地看出：

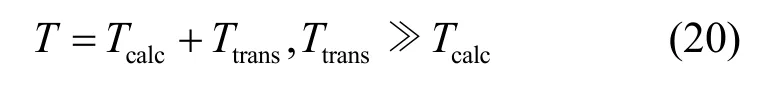
其中，T表示总的时延，Ttrans表示传输时延，Tcalc表示计算时延。因此，故障节点增加所带来的计算时延同传输时延相比是可以忽略的，这里的传输时延同NT节点以及树节点的密度有关，也与故障传感器的数量有关。这使得随着故障节点所占百分比的增加，T呈线性增加。在文献[14]中，计算时延主要发生在传感器正在移动以及最优线性规划 LP的计算过程中。在文献[11]中，随着故障节点的增加，邻接点数据计算的平均值也将成比例的增加，在文献[11]和文献[14]中，这种时延的增加超过50%。

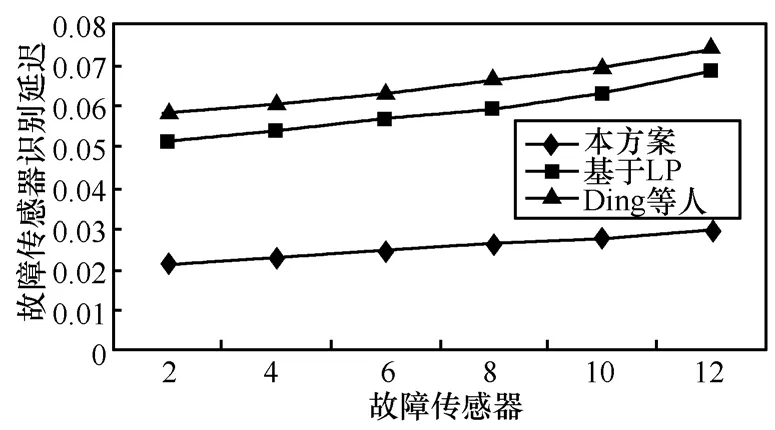
图14 故障传感器识别延迟

5.2.7 负载

随着节点密度的变化，将本文提出的算法与文献[8]的方法进行比较，如图15所示。可以看出，随着节点密度的增加（假设故障节点的数目保持不变）对本文所提出的算法几乎没有影响，这是由于，融合树算法识别故障传感器节点数目保持不变，每个节点只发送故障传感器的值(x, y, f(x, y))到其他树节点，与节点密度的增加无关。与此相反，在文献[8]，随着节点密度的增加，每一故障传感器的邻接节点数目增加，识别故障传感器的分组交换增多。另外，故障传感器在源头没有被检测到，并且会传播给BS，同时还会导致数据负载的增加。

图15 分组负载与网络密度的关系

5.2.8 命中率

图 16显示了本文算法在检测故障传感器时的准确性。可以看出，随着节点密度的增加，命中率平稳递增，构建AT的速度更快，覆盖的范围更大，使得大部分NT节点都是可达的。因此，故障传感器数量的增加（NT节点中的小部分）仍然可以确保大部分NT节点发送数据到最邻近的树节点，同时在早期就可以检测故障节点。命中率可以达到94%。而文献[8]的命中率只有62%。

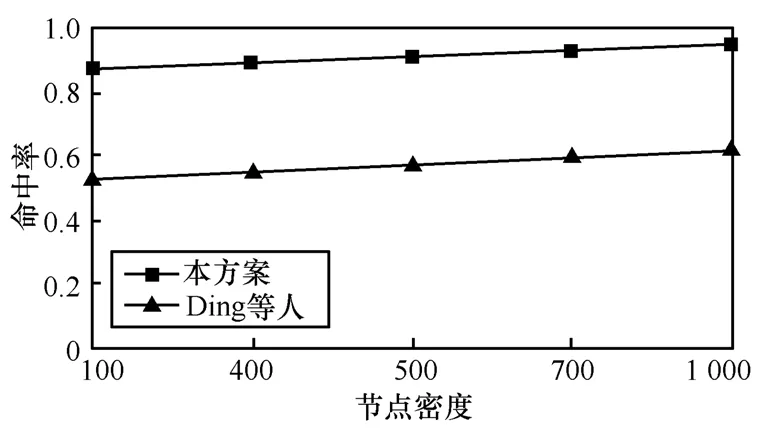
图16 节点密度与命中率的关系

6 结束语

本文针对无线传感器网络中容错事件区域检测问题，提出了一种新的分布式容错检测算法.首先，构建的融合树，使得在缺少传感节点的位置，利用被检测事件的时空相关性，也能获得事件检测的属性值，其错误率控制在可接受的范围内。在此基础上，提出一种基于融合树的事件区域检测容错算法，该算法可以对多个事件进行检测，识别发生在边界区域的事件和有故障的传感器节点，把检测读数传给基站。另外，强调异常事件发生节点的重要性，使得事件区域检测问题，以及事件区域边界节点的错误修正问题得到较好的改善。

[1] 李建中, 李金宝, 石胜飞.传感器网络及其数据管理的概念问题与进展[J]. 软件学报,2003,14(10)∶ 1717-1727.LI J Z, LI J B,SHI S F. Concepts, issues and advance of sensor networks and data management of sensor networks[J].Journal of Software,2003,14(10)∶1717-1727.

[2] 曹冬磊, 曹建农, 金蓓弘.一种无线传感器网络中事件区域检测的容错算法[J].计算机学报,2007,30(10)∶1770-1776.CAO D L,CAO J N,JIN B H.A fault-tolerant algorithm for event region detection in wireless sensor networks[J].Journal of Computer,2007,30(10)∶1770-1776.

[3] 任丰原,黄海宁,林闯.无线传感器网络[J].软件学报,2003,14(7)∶1282-1291.REN F Y,HUANG H N,LIN C. Wireless sensor networks[J].Journal of Software, 2003,14(7)∶1282-1291.

[4] KRISHNAMACHARI B, IYENGAR S S. Distributed Bayesian algorithms for fault-tolerant event region detection in wireless sensor networks[J]. IEEE Trans on Computers, 2004,53(3)∶241-250.

[5] CHEN Q, LAM K Y, FAN P. Comments on, distributed Bayesian algorithms for fault tolerant event region detection in wireless sensor networks[J]. IEEE Transactions on Computers, 2005, 54(9)∶ 1182-1183.

[6] LUO X, DONG M, HUANG Y. On distributed fault-tolerant detection in wireless sensor networks[J]. IEEE Trans on Computers, 2006,55(1)∶58-70.

[7] KOUSHANFAR F, POTKONJAK M, SANGIOVANNI- VINCENTELLI A. On-line fault detection of sensor measurements[A]. Proc of the IEEE Sensors[C]. 2003.974-979.

[8] DING M, CHEN D, et al. Localized fault tolerant event boundary detection in sensor networks[A]. Proceedings of the Annual IEEE Conference on Computer Communications (INFOCOM)[C]. Miami,2005.902-913.

[9] KOUSHANFAR F, POTKONJAK M, SANGIOVANNI-VINCENTELLI A. Fault-Tolerance in Sensor Networks[M]. Handbook of Sensor Networks, CRC Press, 2004.

[10] REN K, ZENG K, LOU W J. Secure and fault-tolerant event boundary detection in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(1)∶ 354-363.

[11] CHEN J, KHER S, SOMANI A. Distributed fault detection of wireless sensor networks[A]. Proc of the 2006 Workshop on Dependability Issues in Wireless Ad Hoc Networks and Sensor Networks (DIWANS 2006)[C]. 2006.65-72.

[12] KOUSHANFAR F, POTKONJAK M, SANGIOVANNI- VINCENTELLI A. Error models for light sensors by statistical analysis of raw sensor measurements[A]. Proc of the IEEE Sensors[C]. 2004.1472-1475.

[13] NOWAK R, MITRA U. Boundary estimation in sensor networks∶theory and methods[A]. Proc of 2nd International Workshop on IPSN[C]. 2003.86-95.

[14] CHINTALAPUDI K K, GOVINDAN R. Localized edge detection in sensor fields[A]. Proc IEEE Workshop on Sensor Network Protocols and Applications[C]. Los Angeles, 2003.59-70.

[15] GUESTRIN C, BODI P, THIBAU R, et al. Distributed Regression∶ an Efficient Framework for Modeling Sensor Network Data[M]. IPSN New York, ACM Press, 2004.

[16] SHARAF A, BEAVER J, LABRINIDIS A, et al. Balancing energy efficiency and quality of aggregate data in sensor networks[J]. The VLDB Journal, 2004, 13(4)∶384-403.

[17] AURENHAMMERF, KLEIN R. Handbook of Computational Geometry[M]. Amsterdam, Netherlands∶ North-Holland, 2000.201-290.

[18] BERTHOLD M. Intelligent Data Analysis[M]. Springer Press,2nd Edition, 2007.

[19] VURAN M C, AKAN O B, AKYILDIZ I F. Spatio-temporal correlation∶ theory and application for wireless sensor networks[J]. Computer Networks, 2004,45∶245-259.