分布式任务调度与副本复制集成策略研究

易侃，王汝传

（1. 南京邮电大学 计算机学院，江苏 南京 210003;2. 中国电子科技集团第28研究所 C4ISR国防科技重点实验室，江苏 南京 210007）

1 引言

数据网格[1]为各种数据密集型的应用提供了一个高性能、大容量、高速传输的并行、分布、广域的计算平台。在数据网格环境下, 任务根据任务调度的结果被提交给计算资源执行，而任务所需要的数据首先通过检索元数据服务和目录服务获取数据副本的位置，然后通过副本选择服务和传输服务获取数据。对于数据敏感的任务，数据的传输时间是任务完成时间的重要组成部分，因此需要副本复制管理动态的调整副本的位置分布，使数据更接近任务所在的计算资源, 从而可以在更短的时间内访问数据，更快地执行任务。

对于数据敏感任务的调度，已有很多将数据相关的因素结合到任务调度中的策略，可以将其分为3个阶段：第1阶段是在资源的选择过程中考虑网络的带宽因素，如文献[2～4]，但是此时任务所需的数据规模较小，任务仍属计算密集型；第2阶段是采用数据驱动的任务调度策略，如文献[5～7]，将数据的大小和数据的位置因素考虑到资源的选择过程中，但这些方法中的数据是固定在某个资源上的单一数据；第3个阶段是集中式的任务调度和数据复制管理集成策略，在任务调度考虑网络带宽和副本位置的同时，通过引入集中式的副本管理机制，动态的创建数据的副本和调整副本的位置，使得任务所需要的数据更靠近它所执行的资源，如文献[8～10]所述，但是在跨多个组织域的实际的网格系统中，集中式的任务调度和数据管理，在可操作性、可靠性和性能上都存在问题，因此有必要研究分布式的任务调度和副本复制管理策略。

为此论文首先提出了数据网格的三层逻辑视图，并基于此视图引出了分布式任务调度与副本复制策略集成的中间件体系结构，然后重点研究了在此分布式架构下，基于博弈论的分布式副本复制策略，最后通过仿真试验验证分布式在线任务调度和副本复制集成策略的有效性和优越性。

2 分布式任务调度和副本复制集成体系结构

类比于 J2EE的三层体系结构，数据网格逻辑上也可以分为3层，图1是数据网格三层的逻辑视图，其中，用户层中的用户是任务的发起者，计算资源层中的计算资源是应用逻辑的执行者，而存储资源层中的存储资源是应用所需数据的管理者。虽然逻辑上是分层的，但是实际上各层之间资源在物理位置上可能是重叠的，比如用户操作的资源可能就是一个计算资源，同样一个计算资源也可以附带一个海量的存储资源。

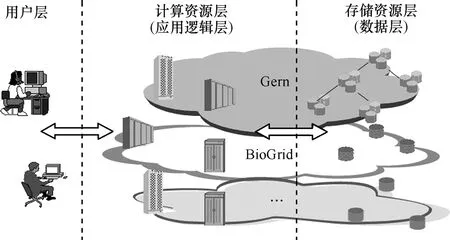
图1 数据网格系统三层逻辑视图

计算网格研究的范畴对应于图1第2层，应用逻辑将会通过资源代理透明地在分布的、高性能的计算资源上执行。当应用需要海量数据时，第3层的存储资源将会为它提供数据支持，数据的检索、传输、可靠性、一致性等都由该层的数据管理功能提供。数据网格需要第2层和第3层的有机集成共同为用户透明地提供高性能的计算和存储资源，其中，第2层与第3层集成的关键是任务调度和副本复制策略的集成。

图2给出了数据网格中分布式的任务调度和副本复制集成体系结构。用户层有多个区域调度器（RS）接收用户提交的任务，每个调度器负责一片自治域的任务请求。多个RS解决了集中式调度器的单点失效问题。当某个 RS的负载过重，那么可以增加新的 RS来分流任务请求，也可以将部分请求分流到其他RS，因此该体系结构有很好的扩展性。

在计算资源层，计算资源收到用户任务请求后，本地调度器（LS）根据本地调度策略为任务分配计算单元，当有任务包含对数据的请求时，本地调度器向本地副本管理器（LRM）请求数据，LRM判断本地存储Cache中是否包含所需数据，如果没有则向远程存储资源广播数据请求，并根据确认请求的返回的信息估算计算资源与存储资源之间的带宽，最后选择访问带宽最大的存储资源获取数据。

在存储资源层，存储资源接收数据请求，如果包含请求的数据则确认该请求。此外，每个存储资源都包含有一个副本管理器（RM），副本管理器能够根据数据的请求情况自主的运行数据副本的复制和删除策略。

图2 分布式的任务和副本复制集成体系结构

3 在线任务调度策略

网格中任务调度分为在线调度方式和批处理调度方式。批处理方式的任务调度算法需要较准确估计任务完成时间，但是对于数据敏感的任务，由于存储资源的传输能力的不确定，网络带宽的不确定等因素，使得副本选择策略运行困难，进而副本的传输时间难以通过启发式的方法估计，另外，由于每个RS只负责部分区域用户的任务请求，在单位时间内接收的任务请求比较少，因此任务调度算法采用在线调度方式[11]即可，即根据当前网格系统的性能、数据的分布情况，为每个到来的任务立刻分配资源。

数据网格中，在线调度方式的任务调度算法的目标是：将任务 ti调度到使其完成时间最短的资源上，即 ∀ mj∈ M , Min(Cij)，其中， Cij表示任务 ti在资源 mj上的完成时间。 Cij= eij+ rj， eij代表任务ti在计算资源 mj上的执行时间， eij= c puij+ n etij，即任务的执行时间为任务所花费的 CPU时间与任务所需数据的传输时间之和，其中，任务 ti数据在计算资源 mj上的准备时间是任务ti所需的数据集合；在以完成时间为指标的任务调度策略中，由于网络带宽的不确定性，通常对数据传输时间的估计采用数据传输的平均带宽，因此Δkj是传输数据 fk到计算资源 mj的平均带宽，但如果任务所需要的数据就在计算资源 mj内，那么传输该数据的时间为0。而 rj代表任务在计算资源 mj上的等待时间，即该资源上等待队列中所有任务的执行时间之和。

4 副本复制的博弈模型

每个存储资源中的副本管理器确定在何时，对哪一个副本进行复制。对于前一个问题，由于计算资源的数据管理器广播数据请求，因此每个存储资源的副本管理器能够统计固定周期内每个数据的请求次数，进而可以获得每个数据的请求频率，其中具有最高请求频率的数据，被称为热点数据，它是被存储资源复制的候选。当同时满足如下2个条件时存储资源将启动数据复制程序：

1) 存储资源中不存在该候选数据；

2) 候选数据请求频率满足某个阈值。

对于后一个问题，实际上是多个存储资源之间竞争复制热点数据的策略选择问题，而博弈论[12]为解决此类非协作竞争实体的策略选择提供了很好的思路。现以2个存储资源 s1、 s2竞争一个热点数据为例，给出该2人博弈的正则形式：存储资源s1、 s2的策略空间都是{0,1}，其中，1代表复制，0代表不复制。采用不同策略组合的 s1、 s2的效益显示在图3的括号内，依据剔除严格劣策略的方法可知，当 s1选择0，而 s2选择1时，该博弈获得Nash均衡解。当博弈的参与者从2个存储资源扩展为m个时，可以定义这m个存储资源数据复制的 Nash均衡。现假设：

1) 存储资源集合为 S = { s1, s2,… ,sm}，它是博弈的参与者，每个参与者的策略空间都是{0,1}，其中，1代表复制，0代表不复制；

2) 计算资源集合为 M = { m1, m2,… ,mn}；

3) 数据集合为 F = { f1, f2, … , fh}；

4) 数据 fk在存储资源 si的状态为 rik∈ { 0,1}，其中，0代表不存在，1代表存在。

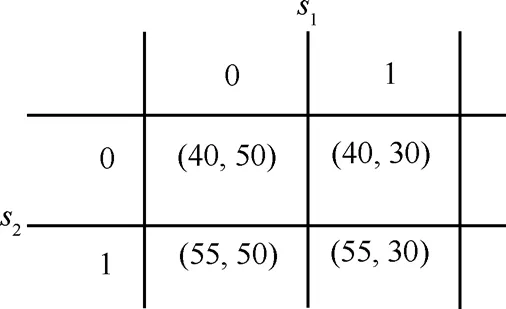
图3 2人博弈的正则形式

定义1 数据复制的Nash均衡。

设 m个存储资源竞争热点数据 fk的博弈的标准式G = { s1, … , sm;u1,… ,um}，如果策略组合 { r *1k,…,r *mk}满足对每一个存储资源 si,r *ik是它针对其他m- 1 个存储资源所选策略 { r *1k,… ,r *i-1k,r *i+1k,… ,r *mk}的最优反应策略，则称该策略组合{r*1k,… ,r*mk}是该博弈的一个Nash均衡解。即

上述定义中效益函数iu并没有确定。通常资源以获取最大的资源利用率为目标，因此每个存储资源都希望计算资源尽可能从它这里访问数据。假设计算资源im从存储资源js访问数据kf的概率为

其中，lij表示计算资源mi与存储资源sj之间的带宽，因此从存储资源sj访问数据fk的平均时延为上述概率的期望：

根据此定义可假设如果计算资源从某个存储资源访问数据 fk的时延越小，那么计算资源选择该存储资源访问数据 fk的可能性越大。由于在博弈的策略选择中，通常如果一个策略的效益越大那么该策略越好，因此取式（2）中| fk| /lij的倒数，即从存储资源 sj访问数据 fk的平均时延重新定义为

令Rj= { rj1, rj2,… rjk, … ,rjh}代表存储资源 sj中副本的状态，若 rjl= 1 ，表示数据 fl已存储在 sj中，而 rjl= 0 表示不存在。由于存储资源 sj的效益只与其存储状态 Rj相关，因此存储资源 sj的效益函数uj定义为

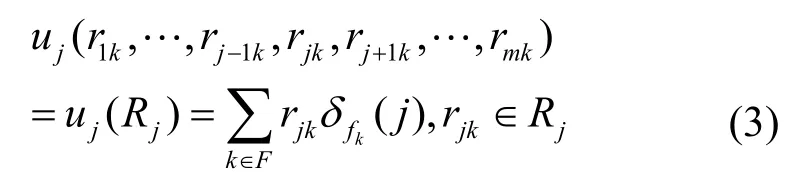
根据纳什定理，若m是有限的，那么该博弈至少纯在一个 Nash均衡，均衡可能包含混合策略。对于m个人，m大于2的博弈，寻找纳什均衡问题不再是一个线性复杂度的问题[13]。

5 Best-Rely算法

由于每个存储资源的空间都是有限的，因此每个存储资源在复制热点数据之前都必须检查其存储空间是否已满。如果其存储空间已满，那么数据替换算法如 LRU算法将被执行以获得足够的存储空间。根据式（3），显然如果每个存储资源的空间都是无限的，那么当它们复制所有的数据将获得最大的效益。然而，存储空间的有限性假设使得复制一个新的副本需要满足：

每个存储资源在复制数据前，可以计算复制前后的存储资源效益，如果存储资源复制数据后的效益高于复制前的效益，那么该存储资源就复制该数据否则不复制，称存储资源单方面选择效益高的策略为最优反应（Best-Reply）策略。可以证明当每个存储资源都采用最优反应策略，那么该策略组合是上述博弈的均衡解。

证明 对于m个存储资源 { s1, …,si,…,sm}，每个存储资源中副本的状态为 { R1, … ,Ri,…,Rm}，假设在复制数据 fk以及删除一些数据后，副本的状态变为 { R1′, …,Ri′ ,…,Rm′}。由 Best-Reply算法的定义可知：

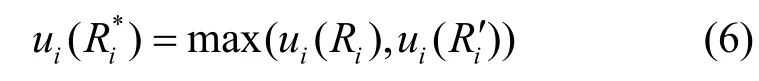
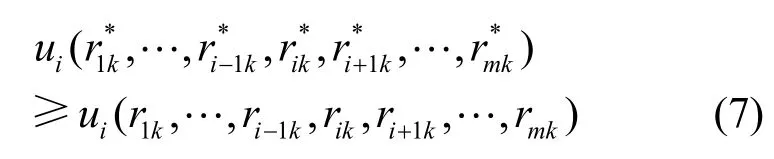
每个存储资源的 RPM 将自动运行 Best-Reply算法以确定是否复制新的数据文件，算法描述见算法1。第2)～6)步统计所有文件的访问频率，并选择访问频率最高的文件kf；第7)～10)步设置存储资源的状态 Rj；第11)步计算存储资源当前的效益函数；第 13)～20)步假设复制文件 fk，存储资源的状态从Rj转到 R'j，并计算新状态下存储资源的效益函数；第21)～24）步如果存储资源复制文件 fk后能够提升效益，那么就复制该文件，并删除被替换的文件。算法Best-Reply描述如下。

算法1 存储资源sj的Best-Reply算法

6 仿真实验

6.1 仿真平台

为验证不同任务调度算法和副本复制集成策略的对任务执行性能的影响，拟对如下的算法组合进行仿真实验：

1) 在线任务调度算法，但无副本复制算法，简记为OTS；

2) 集中式任务调度和副本复制集成策略[9]，简记为OTS+CDR；

3) 分布式的在线任务调度算法与总复制（AR,always replica）副本复制集成策略，简记为OTS+AR；

4)分布式在线任务调度算法与Best-Reply（BR）算法的集成策略，简记为OTS+BR。

为此，设计并开发了一个基于GridSim[14]的网格任务调度仿真平台（GJSSP, grid job scheduler simulation platform），GJSSP能够可视化地创建、改变和保存网格仿真环境，其内建的用户系统，任务调度系统和副本复制管理系统能够使算法的设计人员只需关心算法设计本身。GJSSP的主界面如图4所示，其中，圆形代表一个资源，长方形代表一个路由器，每条线代表一条链路。这3个组件都能够被随意拖动并且可以修改其属性。在点击“generator”按钮后，GJSSP将产生一系列配置文件，这些配置文件将在仿真执行前被解析并创建相应的GridSim实体对象。

图4 GJSSP主界面

仿真所需主要的配置文件及其属性，如表1所示，其中，1代表只有一个配置文件，*表示可以由1个或多个配置文件，表中的作业属性配置文件和文件属性配置文件是通过工具自动生成，主要参数如表中所示，其他配置文件是通过GJSSP的可视化界面配置。

表1 配置文件及其属性

6.2 仿真结果

在任务的计算量和数据量都是海量的情况下，对数据复制策略影响最大的是数据文件总量与存储空间总量的比例。因此，拟对该比例λ为1/10和1/100的2种情况，前者存储空间相对与数据总量较小，而后者则相对较大，在如下2个指标上进行讨论：

根据图5和图6，由于OTS没有采用副本的复制策略，数据总是从某些固定存储资源获取，需要过多的数据请求时间，因此无论存储资源是否充裕，它的平均任务用时最多。当λ=1/100时，OTS+AR的用时最少，这主要因为计算资源所需要的数据总是被复制到离它最近的存储资源上，在存储空间充裕时能够显著的减少数据请求时间，但当λ=1/10时，总复制策略对任务的执行起到反作用，平均完成作业时间显著增长。另外，利用OTS+BR算法的平均任务完成时间始终比利用OTS+CDR算法多，这主要是因为在仿真环境下集中式副本复制策略在估算计算资源和网络资源的性能较为精确，因此副本位置的优化比较准确，而分布式的副本复制策略只根据有限信息优化副本位置，与全局优化策略相比效果较差。

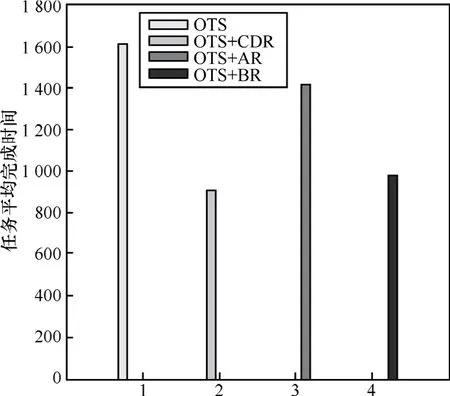
图5 当λ=1/10时的任务平均完成时间

图6 当λ=1/100时的任务平均完成时间

由于平均网络负载越小、越稳定，那么算法越好。根据图7，当λ=1/100时，OTS算法的平均网络负载较高，且呈缓慢下降态势，但是其负载仍然要优于OTS+CDR算法和OTS+BR算法。利用OTS+BR算法的平均网络负载较低但不够稳定。当λ=1/10时，利用 OTS算法的平均网络负载形状变化不大，相反利用 OTS+AR算法的平均网络负载形状变化很大，即 OTS+AR算法对存储资源的空间大小较为敏感，而图7所示利用OTS+CDR与OTS+BR算法的平均网络负载对于存储资源空间的大小较不敏感。因此OTS+BR算法与OTS+CDR算法相比，虽然增加了一定任务平均完成时间，但是它具有更好的扩展性，仿真结果表明它完全可以取代OTS+CDR算法。

图7 平均网络负载比较

7 结束语

论文首先提出了3层的分布式任务调度和数据管理体系结构，在此分布式体系结构下，对在线任务调度算法和基于博弈论的副本复制的集成策略在自行研发的网格仿真平台上进行仿真实验，并同其他3类算法组合在平均任务完成时间和平均网络负载2个指标上进行了比较。结果表明：1)仅仅在线任务调度算法不能满足数据密集型任务对执行性能的要求，其平均任务完成时间最高，网络负载不平衡；2）总复制的副本复制算法虽然在存储空间充分时具有最少的平均任务完成时间和最低的网络负载，但是当存储空间较小时，上述指标均呈现明显的增长；3）分布式的 OTS+BR算法在调度效果上比集中式的OTS+CDR稍差，但其平均网络负载对存储空间大小不敏感，而且算法的扩展性更好，因此完全可以替代集中式的OTS+CDR算法。

[1] SRIKUMAR V, BUYYA R, RAMAMOHANARAO K. A taxonomy of data grids for distributed data sharing, management, and processing[J].ACM Computing Surveys, 2006,38(1)∶ 3-13.

[2] BEAUMONT O, CARTER L, FERRANTE J, et al. Bandwidth-centric allocation of independent tasks on heterogeneous platforms[A]. International Parallel and Distributed Processing Symposium[C]. Marriott Marina, Fort Lauderdale, Florida, 2002. 79-88.

[3] LARS-OLOF B, HANS-ULRICH H, CESAR A. Performance issues of bandwidth reservations for grid computing[A]. 15th Symposium on Computer Architecture and High Performance Computing(SBAC-PAD'03)[C]. Sao Paulo, Brazil, 2003. 82-91.

[4] 季一木, 王汝传. 基于粒子群的网格任务调度算法研究[J].通信学报,2007,28(10)∶ 60-67.JI Y M, WANG R C. Study on PSO algorithm in solving grid task scheduling[J]. Journal on Communications, 2007,28(10)∶ 60-67.

[5] SIVARAMAKRISHNAN N, TAHSIN K, UMIT C, et al. Database support for data-driven scientific applications in the grid[J]. Parallel Processing Letters, 2003,13(2)∶ 245 -271.

[6] LE H. CODDINGTON P, WENDELBORN A. A data-aware resource broker for data grid[J]. Lecture Notes in Computer Science, 2004,32(22)∶ 73-82.

[7] KOSAR T. A new paradigm in data intensive computing∶ stork and the data-aware schedulers[J]. Challenges of Large Applications in Distributed Environments, 2006, 25(4)∶ 5-12.

[8] NHAN N, SANG B. Combination of replication and scheduling in data grids[J]. IJCSNS International Journal of Computer Science and Network Security, 2007,7(3)∶ 304-308.

[9] CHAKRABARTI A, SHUBHASHIS S. Scalable and distributed mechanisms for integrated scheduling and replication in data grids[J].Distributed Computing and Networking, 2008,8(2)∶ 227-238.

[10] NHAN N, DANG H, LIM S. Improvement of data grid's performance by combining job scheduling with dynamic replication strategy[A].Grid and Cooperative Computing 2007(GCC 2007)[C]. Urumchi, Xinjiang, China, 2007.513-520.

[11] MAHESWARAM M, ALI S, SIEGEL H, et al. Dynamic matching and scheduling of a class of independent tasks onto heterogeneous computing systems[A]. Heterogeneous Computing Workshop(HCW99)[C].1999.30-44.

[12] 施锡铨. 博弈论[M]. 上海∶ 上海财经大学出版社, 2000.SHI X Q. Game Theory[M]. Shanghai∶ Shanghai Finance University Press,2000.

[13] CONSTANTINOS D, PAUL W, CHRISTOS H. The complexity of computing a nash equilibrium[A]. Proceedings of STOC (2006)[C].Seattle, WA, USA, 2005. 89-97.

[14] MURSHED, RAJKUMAR B, MANZUR. Gridsim∶ a toolkit for the modeling and simulation of distributed resource management and scheduling for grid computing[J]. Concurrency and Computation∶Practice and Experience (CCPE), 2002,14∶ 13-15.