铁路线路的归一化放样

姜晨光 路 奎 林长胜 蔡香玲 杨英姿 朱烨昕

(1.江南大学环境与土木工程学院,江苏无锡 214122；2.山东省国土测绘院,山东济南 250013；3.烟台建设集团钢结构有限公司,山东烟台 264003；4.文登市建设局,山东文登 264400；5.山东宜华咨询有限公司,山东威海 264200；6.无锡市建设局,江苏无锡 214031)

1 概述

铁路轨道几何形位的科学性与准确性是确保铁路列车行车安全的关键之一,要确保铁路轨道几何形位的准确性就必须依靠精细、高精度的测量技术。铁路轨道几何形位的基本要素包括轨距、水平、前后高低、轨向、轨底坡、曲线轨距加宽、曲线外轨超高、缓和曲线、限制坡度、竖曲线等。轨道的几何形位应按静态与动态两种状况进行管理。静态几何形位是轨道不行车时的状态,采用道尺等工具进行测量。动态几何形位是行车条件下的轨道状态,采用轨道检查车进行测量。曲线轨距加宽(高速铁路一般不加宽)的方法是将曲线轨道内轨向曲线中心(圆心)方向移动,曲线外轨的位置则保持与轨道中心半个轨距的距离不变。曲线轨距的加宽值与机车车辆转向架在曲线上的几何位置有关。外轨超高度是指曲线外轨顶面与内轨顶面水平高度之差。铁路缓和曲线及圆曲线的准确定位是铁路轨道几何形位确定中的关键工作,铁路缓和曲线及圆曲线通常会给出曲线方程式,这些曲线方程式采用的都是数学坐标系坐标(比如圆曲线方程式以圆心为坐标原点、缓和曲线方程式以曲线起点为坐标原点),而铁路测量与放样时采用的是国家坐标系,故传统的缓和曲线及圆曲线放样方法是先确定曲线的起点、再按偏角法或切线支距法或弦线支距法或直角坐标法编制放样数据表、然后再按与数据表对应的方法进行放样。

传统的缓和曲线及圆曲线放样方法具有速度慢、效率低、精度不高、过程繁琐等诸多弱点,可否实现缓和曲线及圆曲线的精准快速放样,笔者及项目组在实践的基础上提出了铁路线路归一化放样的思想,并在实际应用中取得了良好的效果,在此做一介绍。

2 铁路缓和曲线及圆曲线的基本特征

缓和曲线是设置在直线和圆曲线之间或半径相差较大的两个转向相同的圆曲线之间的一种曲率连续变化的曲线。缓和曲线的作用是曲率连续变化、便于车辆遵循,离心加速度逐渐变化满足旅客舒适要求；超高横坡度及加宽逐渐变化使行车更加平稳,与圆曲线协调配合增加了线形的美观度。对缓和曲线的基本要求是可行性好、缓和性好、计算方便且公式简单(便于在设计、施工中使用)。铁路设置缓和曲线的目的是在曲线到直线、直线到曲线上,为使作用力不突变(平面上),平面曲线曲率 ρ应由∞→R；同时,使超高h在缓和曲线上逐步完成长度要求,其中L0为缓和曲线长度。缓和曲线的主要形式有三次抛物线、高次抛物线(4,5,7次抛物线)、三角函数线、双纽线、回旋线、等。

2.1 回旋线

回旋线(见图1)是曲率随着曲线长度成比例变化的曲线,其基本公式为

式(1)中,r为任意点曲率半径/m；l为起点到任一点的曲线长/m；A为长度量纲。r、l称回旋线参数,它表示回旋线曲率变化的缓急程度。在缓和曲线终点处 l=L0、r=R,因此,有

回旋线的性质可概括为4点,即曲率按线形函数增大k=1/r=l/A2(A越大、曲率k越小、回旋线变化越慢；A越小、曲率k越大、回旋线变化越快)；所有回旋线都是几何相似的；切线角 β与曲线长l的平方成正比；极角 δ近似为 β/3。

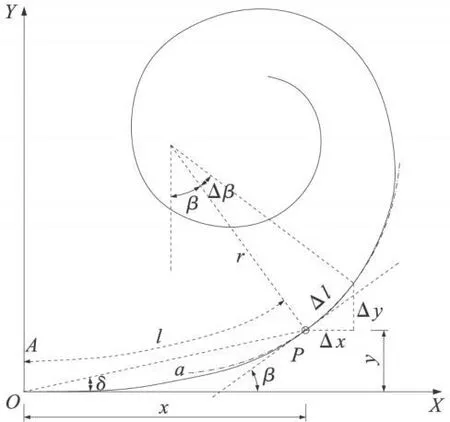
图1 回旋线及其各相关要素

2.2 三次抛物线

三次抛物线的形式为

三次抛物线用作缓和曲线只能在 β≤24°的条件下使用。由于缓和曲线长度的确定主要考虑安全和舒适2个因素,因此,高速铁路线路缓和曲线的设置条件是L0应足够长,顺坡两端要圆顺,要保证缓和曲线的曲率变化率为常量。现在,我国采用圆曲线来过渡,缓和曲线的曲率半径变化率c为

式(4)中,L0为缓和曲线的长度,R为圆曲线半径。

我国高速铁路线路最小曲线半径取50 m的整倍数,新建客运专线不同速度下的推荐圆曲线半径见表1。客运专线线路的夹直线、圆曲线最小长度见表2(其中vmax为火车最大运行速度)。另外,铁路通过设置竖曲线以限制向上的离心加速度,客运专线不同速度下的最小竖曲线半径见表3,考虑运行安全性要求的竖曲线半径见表4,应用时一般综合表3和表4数值(即取2表中相应的大值)。

表1 客运专线不同速度下的圆曲线半径

表2 客运专线线路夹直线、圆曲线最小长度

表3 客运专线不同速度下的最小竖曲线

表4 考虑运行安全性要求的竖曲线半径

2.3 不同类型缓和曲线的特点

双纽线(方程式为r=c/a)在极角为45°时曲率半径最小,此后半径增大至原点,全程转角达到270°。回旋线、三次抛物线和双纽线在极角较小(5°～6°)时几乎没有多少差别。随着极角的增加,三次抛物线的长度比双纽线的长度增加得快些,而双纽线的长度又比回旋线的长度增加得快些。回旋线的曲率半径减小得最快,而三次抛物线则减小最慢。从保证火车平顺过渡的角度看,三种曲线都可以作为缓和曲线。目前我国铁路采用三次抛物线。

3 铁路线路的归一化放样方法

铁路线路归一化放样方法实现的前提是将铁路线路设计中所有的非国家坐标系统的线路坐标(比如铁路圆曲线以圆心为坐标原点的坐标系统、缓和曲线以曲线起点为坐标原点的坐标系统等)转换为国家坐标(高斯坐标)。假设某点的非国家坐标系统线路坐标为X′、Y′,该点在国家坐标系统中的对应坐标为 X、Y,则其坐标转换模式为

式(5)中,ΔX0、ΔY0、m 、θ,分别为 2 个平面坐标系间的平移、尺度、旋转参数,总称为平面转换四参数。不难看出,要求出平面转换四参数至少需要2个公共点。即先根据铁路线路设计图(CAD图)获得非国家坐标系统线路坐标中2个线路点的国家坐标(可在设计图上直接获得,也可利用Auto CAD的ID命令捕捉获得,2个线路点一般应为曲线的起终点或应相距尽可能地远)Xi、Yi,然后再根据2个线路点的线路设计坐标(即非国家坐标系统坐标或数学坐标)Xi′、Yi′借助式(5)即可求出平面转换四参数,进而可将该非国家坐标系统线路坐标中各个线路点的设计坐标转换为国家坐标,然后就可利用铁路线路测量控制网中的控制点对所有的非国家坐标系统的线路设计点进行放样(采用电子全站仪或 GPS)从而摒弃传统的放样方法。

由于铁路线路一般很长,常跨越若干个高斯投影带,因此,坐标换带就成了必须重视的工作。另外,当线路点放样精度要求较高且高斯投影变形又较大时,还应移动中央子午线位置以建立独立的工程放样控制网(比如特大桥控制网)。同时,采用GPS放样时还存在GPS坐标与国家坐标的转换问题及GPS高程与正常高的转换问题。上述种种情况决定了铁路线路归一化放样过程中必须熟悉大地坐标与高斯坐标间的相互转换、GPS坐标与国家大地坐标间的相互转换以及坐标换带等基本理论并采用高精度的转换方法。要实现上述高精度转换,笔者建议采用以下公式。

图2 GPS坐标与国家大地坐标间的关系

3.1 GPS坐标与国家大地坐标的转换

如图2,GPS测量的坐标系是世界大地坐标系即WGS-84坐标系,而我国目前常见的三维坐标系为1954北京坐标系及1956黄海高程系,或1980国家大地坐标系及1985国家高程基准以及2000国家大地坐标系,故必须对GPS测量的三维定位成果必须进行换算,才能满足铁路测量的实际需要。GPS坐标与国家大地坐标间的转换至少采用七参数转换法,七参数转换法需转换区域内至少有3个已知国家坐标的控制点(3个已知控制点应均匀分布在转换区域的边缘附近),在这些国家控制点上获取载波相位静态观测1～2 h的WGS-84系坐标(X,Y,Z)成果,再根据数学模型(见式(6))解算出七个转换参数,然后即可对该转换区域内所有的点进行2个不同坐标系间坐标的相互转换。

式(6)中,Xi、Yi、Zi为国家坐标系的三维空间直角坐标；X、Y、Z为GPS的WGS-84系三维空间直角坐标；ΔX、ΔY、ΔZ为两坐标原点间的平移参数(或叫原点距 )；K 为两坐标系间的尺度比；εx、εy、εz为两坐标系坐标轴间的旋转角(旋转参数)。

3.2 GPS高程与国家高程的转换

GPS高程是基于WGS-84椭球的大地高高程(简称大地高),我国采用的高程系统则为正常高。GPS大地高是由地面点沿法线到WGS-84椭球体面的距离,正常高是地面点沿铅垂线到似大地水准面的距离。将GPS测定的大地高转为正常高的关键是求取大地高H与正常高h间的差值(即高程异常值 ξ)。其高程转换的基本数学模型为

推算 ξ值的方法很多,常用的有GPS水准高程法和GPS重力高程法等。GPS水准高程方法又可分为平面拟合法、二次曲面拟合法、多面函数法、样条函数法等。GPS重力高程方法则包括地球重力场模型法、重力场模型与GPS水准结合法、地形改正法等。具体应根据工区范围大小及地形条件(比如平地、丘陵地、山地或高山地、等)选择相应的有效方法。实践证明,在局部GPS网中宜采用GPS水准高程拟合法(100 km2以内平坦地区平面拟合法的拟合精度优于4cm),在高程异常变化有规律的地区且已有控制点分布较均匀的情况下宜用二次曲面拟合法或高次多项式曲面拟合法(拟合精度可优于3 cm),大区域宜用重力场模型与GPS水准相结合的方法。

(1)平面拟合法

平面拟合法基本公式为

式(8)中,ξi为已知的某公共点(同时具有GPS大地高和国家高程的点)高程异常；xi、yi为某已知公共点相应的平面直角坐标；a1、a2、a3为待求的模型参数。当已知公共点为3时可直接求出a1、a2、a3值,若公共点的数目大于3则应采用最小二乘法解算a1、a2、a3,其相应误差方程式为

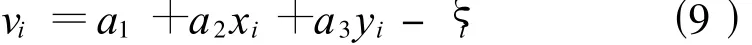
用矩阵的形式则可表示为根据最小二乘原理可求得

(2)二次曲面拟合法

二次曲面拟合法的基本公式为

式(12)中 ,a0、a1、a2、a3、a4、a5为模型待定参数 ,不难理解,转换区域内至少应有6个公共点。当公共点多于6个时,仍应组成误差方程(见式(10))按最小二乘原理求解转换参数 a0、a1、a2、a3、a4、a5。此时式(10)中的 X 、A 为

(3)高次多项式曲面拟合

高次多项式曲面拟合是二次曲面拟合法进一步扩展的结果,此时的数学模型为

显然,式(13)的误差方程矩阵式仍可参照式(10)扩展列出。

(4)地球重力场模型与GPS水准结合法

方法的实质是在GPS水准点上,将由GPS大地高和水准正常高求得的高程异常 ξi与由重力场模型求得的高程异常 ξmi进行比较,求出其差值 δξi,即

然后再采用二次曲面拟合方法,由已知点的平面坐标(xi,yi)和 δξi推求其他点 K上的 δξk,进而可计算出待测点的正常高HK,计算公式为

3.3 大地坐标(B,L)转换为高斯平面直角坐标(X,Y)

换算数学模型(即高斯投影正算公式)为

式(17)中,B为投影点的大地纬度；l=L-L0(L为投影点的大地经度,L0为轴子午线(中央子午线)的大地经度)；N为投影点的卯酉圈曲率半径；t=tan B；η=e′cos B(e′为椭球第二偏心率 ,e′2=(a2-b2)/b2,a 、b分别为参考椭球的长、短半径)。当l=0时,X0为从赤道起算的子午线弧长,其计算公式为

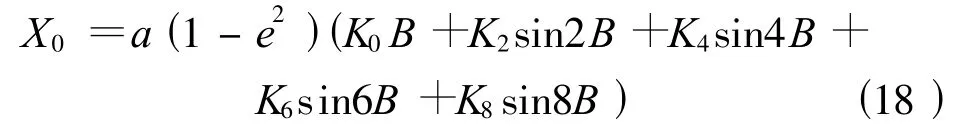
式(18)中 ,K0、K2、K4、K6、K8为系数 ,其中

式(19)～式(23)中,e为椭球第一偏心率,e2=(a2-b2)/a2。

3.4 高斯平面直角坐标(X,Y)换算地理坐标(B,L)

换算的数学模型(即高斯投影反算公式)为

式(24)中,Bf为投影点的纬度(或称底点纬度),其计算公式为

式(25)中,B0=X/[a(1-e2)A0](X为y=0时对应的子午线弧长)；Ka、Kb、Kc、Kd的计算公式为

第一基本纬度函数W=(1-e2sin2B)1/2、第二基本纬度函数为 V=(1+e′2cos2B)1/2、B为大地纬度；子午圈曲率半径为M=a(1-e2)/W3=c/V3；卯酉圈曲率半径为N=a/W=c/V；平均曲率半径为Rm=(MN)1/2=c/V2；任意方向法截弧的曲率半径为 RA=Rm-[Rme′2cos B cos(2A)]/2=Rm+Δ(其中 A 为任意方向的方位角 ,Δ=-[Rme′2cos B cos(2A)]/2)。

3.5 坐标换带

换带的数学模型分2种情况,当 Δy1≤60 km时计算公式为

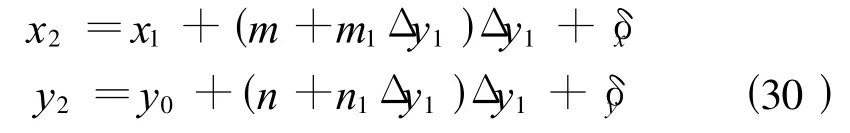
当 Δy1＞60 km时计算公式为

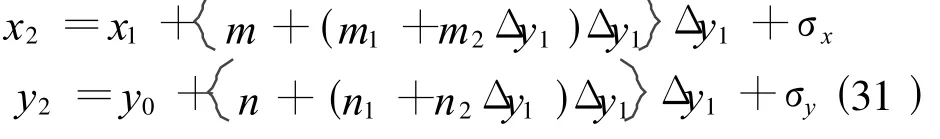
应用式(30)、(31)时,x1、y1为换带前的已知坐标,x2、y2为换带后的坐标,由西带向东带换带时y2取负值,由东带向西带换带时y2取正值。式(30)、(31)中,y0恒取正值；Δy1=±y1-y0(西带换至东带时y1前取 +号、东带换至西带时 y1前取取 -号)；δx=(4 γ0)-D sin(4 γ0)；m3=[5y0sin(2 γ0)]/(8R)；n=-

4 结束语

本文提出的铁路线路归一化放样方法可极大地简化铁路线路放样的过程,提高铁路放样的精度,为现代化测绘仪器(比如GPS、电子全站仪)在铁路线路放样中的便利应用奠定坚实的理论基础,符合现代化放样的历史潮流。在应用本文所述方法时一定要分清各种各样坐标系统、高程系统的特点及相互关系,一定要认真仔细地进行不同坐标系统、不同高程系统间的归一化转换,同时应注意满足铁路放样中的精度要求,为铁路的高标准、高质量建设提供优质的测绘保障。

注：本研究项目得到国家自然科学基金(79160173)的支持,在此表示感谢！

[1]铁道部.高速铁路隧道[M].北京：中国铁道出版社,2006

[2]铁道部.铁路工程设计规范使用手册[M].北京：中国铁道出版社,2006

[3]刘统畏.建造师执业手册：铁路工程[M].北京：中国建筑工业出版社,2006

[4]李成辉.轨道[M].成都：西南交通大学出版社,2005

[5]郝 瀛.铁道工程[M].北京：中国铁道出版社,2000

[6]王午生,许玉德,郑其昌.铁路与城市轨道交通工程[M].上海：同济大学出版社,2002

[7]张 未.跨区间无缝线路[M].北京：中国铁道出版社,2001

[8]许实儒.轨道基本理论[M].北京：中国铁道出版社,1999

[9]GB50308—1999 地下铁道、轻轨交通工程测量规范[S]

[10]李青岳,陈永奇.工程测量学[M].北京：测绘出版社,1995

[11]GB50307—1999 地下铁道、轻轨交通岩土工程勘察规范[S]

[12]TB10012—2001 铁路工程地质勘察规范[S]

[13]CJJ8—99 城市测量规范[S]

[14]CH1002—95 测绘产品检查验收规定[S]

[15]CH1003—95 测绘产品质量评定标准[S]

[16]GB50026—93 工程测量规范[S]

[17]CH2001—92 全球定位系统(GPS)测量规范[S]