断索导致的斜拉桥结构易损性分析

于 刚,孙利民

(同济大学 土木工程防灾国家重点实验室,上海 200092)

自2001年9月11日纽约世贸大厦遭到恐怖袭击倒塌以后,各国学者更加关注结构损伤与其后果之间的关系.

英国Bristol大学的研究者[1-3]基于图论对桁架从结构几何构成角度作了拓扑易损性的研究.在国内,刘西拉[4-6]较早进行了结构易损性的研究,将结构易损性定义为结构在突发事件中容易受到伤害或者损伤的程度.柳承茂[7]对桁架结构的结构易损性进行了定量的分析研究,在结构拓扑分析和失效场景两个方面进行了探讨.Yu G等[8-9]做了结构易损性分析在结构健康监测中应用的研究.虽然在结构不成比例倒塌研究方面取得了大量的研究成果,但是由于结构损伤与成因之间的关系受到结构体系自身材料以及拓扑构成的影响,且不同荷载作用下又有不同的表现形式,使不成比例破坏的量化研究的难度加大,目前仍然处于探索阶段,还没有形成比较统一的理论体系.

一些国家的结构规范给出了对提高结构鲁棒性的定性要求[10],这些规定都缺乏定量分析基础,没有相应的计算方法和构造措施,因此在应用时难以保证定性目标的实现.

作为生命线工程的桥梁结构,容易成为恐怖袭击的目标[11].本文主要研究斜拉桥拉索在极端事件中破断后引起的结构性能的变化,从易损性分析角度评价斜拉桥体系结构性能对不同位置拉索破断的损伤场景的敏感性,为斜拉桥工程设计、监测和养护管理提供参考.

1 斜拉桥断索易损性分析方法

结构的易损性定义为结构性能对局部损伤的敏感性.从易损性定义可知,结构性能对局部损伤的敏感性越高,则易损性越高,对局部损伤的敏感性越低,则易损性越低.为了进行量化描述,首先要定义两个参数:一是损伤场景对结构性能的影响程度C;另一个是损伤场景占结构体系总体规模的比例M.如果结构体系的性能指标用P表示,对结构性能的基本要求用表示,则对于完好结构有P≥.在损伤场景D发生后,结构性能降为PD,则此损伤场景对结构性能的影响程度CD可定义为

若损伤场景D对结构性能没有影响,则 PD=P;若损伤场景发生后,结构体系失效,则PD=0.因此,CD=[0,1].

本文考察结构对不同拉索断裂的损伤场景的易损性,因此将M表示成归一化的描述不同损伤场景的相对规模大小的参数,其取值范围为MD=[0,1].有了这两个参数,易损性的量化分析可划分为三大步骤:一是根据外界可能出现的破坏事件确定损伤场景;二是对各个损伤场景求取结构性能影响程度C和占结构体系总体规模的比例M这两个参数;最后,利用这两个参数进行损伤场景的易损性评价.

本文将损伤场景D定义为斜拉桥结构在某个破坏事件中一根或多根斜拉索发生破断.由拉索破断损伤场景导致主梁的失效主要有两种模式,一是截面局部应力超过材料应力强度极限,二是主梁节段在轴向压力作用下发生屈曲失效破坏.因此,本文以主梁最小屈曲安全系数λ和最大应力安全系数μ作为结构性能参数,结构性能约束函数可表示为

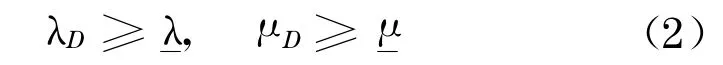
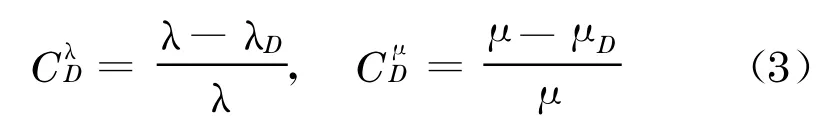
对拉索破断损伤场景占结构体系总体规模的比例M表示为

式中:AD表示损伤场景中拉索截面面积;A表示斜拉桥中所有拉索截面面积之和.

每一个损伤场景都对应着一对C,M值,而根据易损性的定义,结构体系对不同损伤场景易损性公式遵循如下关系:

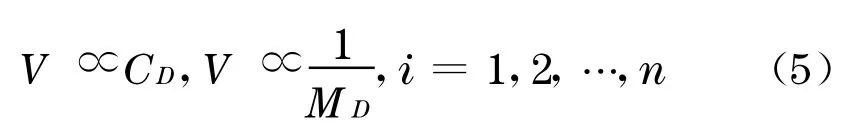
式中:V为结构体系的易损性指数.结构对各损伤场景的易损性与损伤场景对结构性能的影响程度成正比,与损伤场景占结构体系总体规模的比例成反比.为了找出对结构性能影响程度C尽可能高,而占结构体系总体规模的比例M尽可能低的易损场景,这里引入由意大利经济学家Vilfredo Pareto提出的多目标帕罗托优化分析方法.帕罗托最优指的是这样一种状态:假设以两个条件F1,F2约束下的资源分配,不能出现在不损害F2(F1)的情况下使得约束条件F1(F2)得到更好的满足.借用这个概念,对多个损伤场景进行评价选取易损场景的问题就可表示为以损伤场景为离散变量的多目标优化问题.设计变量为由损伤场景组成的向量 D=(D1,D2,…,Dn)T,评价损伤场景易损性的目标函数表示为F=(F1,F2)其中

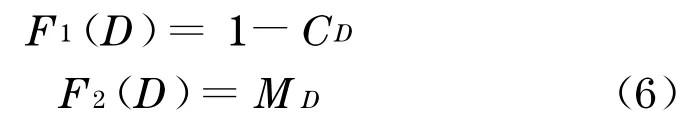
则此双目标优化问题可以表达为如下形式:

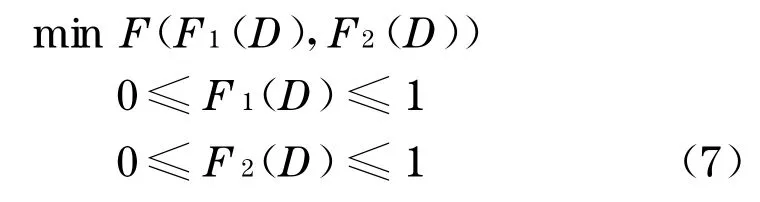
有上述优化模型之后,各个易损场景就是分布于F1,F2坐标平面上的离散点,对于此双目标优化问题的求解可利用图1加以说明.符合上述优化问题约束条件的解称为非劣解,非劣解的连线称为帕罗托边界,如图中实线所示.

图1 非劣解图示Fig.1 Exam p le o f nonin ferior solution

在寻求以F1,F2最小为目标的解的情况下,离散点C不是此最优问题的非劣解,因为存在点A比点C在优化目标上绝对占优;而点 A和B都不能互相绝对占优,因此这两点都是此最优化问题的非劣解.根据非劣解的性质,可采用如下算法确定非劣解集.用D0表示某一损伤场景,Di表示损伤场景集合Ω中除D 0外任一损伤场景,对D0是否为非劣解可根据如下三种情况进行判断:

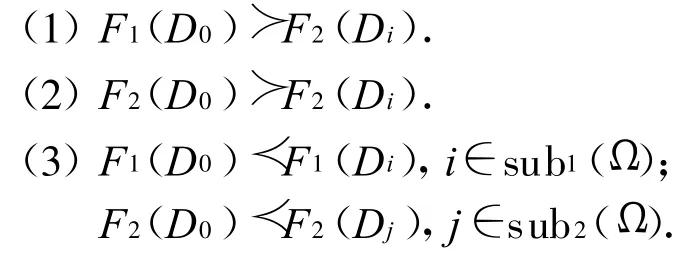
式中:a(1)≻a(2)表示对同一目标函数,变量1的函数值优于变量2的函数值.sub1(Ω),sub2(Ω)表示损伤场景集合 Ω的子集.若D0满足上面第(1)或第(2)种情况,则可直接判断为非劣解;若D0满足第(3)种情况,则需要进一步判断:若 sub1(Ω)∩sub2(Ω)=Ø,则为非劣解,否则不是非劣解.

下面结合结构性能参数求取方法和算例分析说明此分析方法的实现过程.

2 斜拉桥主梁屈曲安全系数

斜拉桥主梁可近似看成两端铰接的弹性支承上的连续梁(图2),采用Engesser的近似方法[12]进行计算.斜拉桥主梁发生屈曲时会形成若干个半波,考察其中一个半波的受力情形.

图2 两端铰接弹性梁Fig.2 H inge-join ted elastic beam

假定其挠曲线为余弦曲线,即

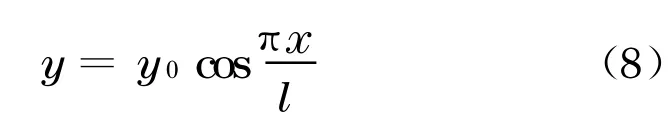
假定半波范围内拉索间距相同均为a,单根拉索竖向支承刚度为k,则弹性支承的等效弹性介质系数可表示为

弹性支承反力与挠度成正比

式中:R为弹性支撑反力;β为拉索支承等效弹性介质系数.

波节点的剪力

中点弯矩为

利用边界条件

得

式中:E为材料弹性模量;I为梁截面惯性矩.由d P/d l=0,易得P值最小时

将式(15)代入式(14)得到临界轴力为

接下来则是要获得斜拉索的等效弹簧刚度k,可参见图3中几何关系获得.

图3 拉索变形几何关系Fig.3 Geom etrica l deformation o f cables

式中:δ1,δ2分别为单位力在A点的索伸长竖向分量和塔弯曲产生的索竖向位移分量;α为索与梁的夹角;lc为拉索长度;AcEc为拉索轴向拉伸刚度;γ为索塔刚度比;EtIt为塔弯曲刚度.

斜拉桥桥塔的弯曲刚度E t I t随着塔高是变化的,因此在计算过程中要得到与每个拉索相应位置的等效抗弯刚度,可以在拉索连接位置加单位力,根据悬臂梁端部力与变形之间的关系获得.如图4所示,在拉索连接点B,单位力作用下桥塔产生横向变形为δ,则桥塔等效抗弯刚度为

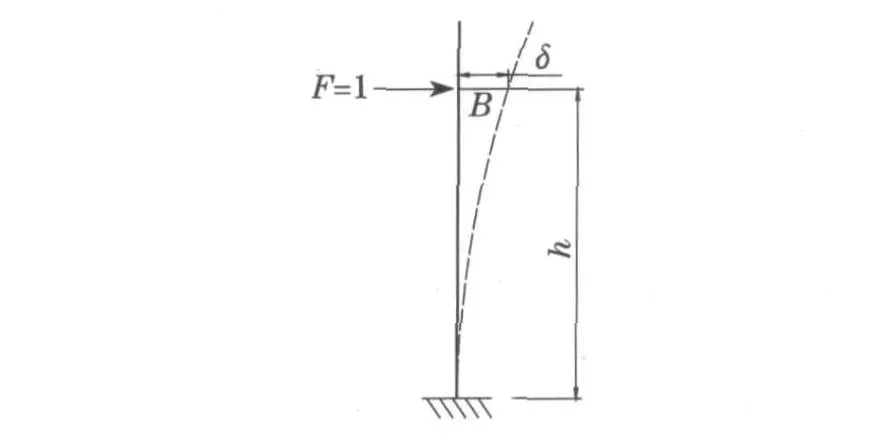
图4 桥塔等效抗弯刚度计算Fig.4 Equivalent flexural rigidity calculation

根据式(17),由k可导出等效β值.考虑到斜拉桥主梁弹性模量E,截面惯性矩I以及拉索支承等效弹性介质系数β是主梁水平坐标x的函数,可将斜拉桥主梁面内稳定临界轴力表示为

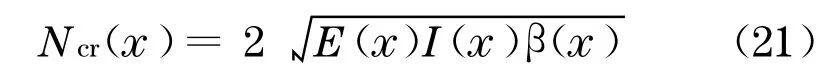
临界轴力与该处梁的实际轴力N(x)之比成为该点的名义屈曲安全度,可取其最小值作为加劲梁的屈曲安全系数.

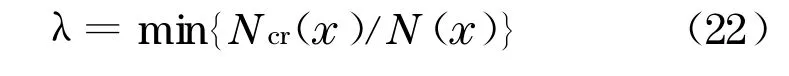
3 算例分析

3.1 斜拉桥概况

本文以某双塔单索面组合梁斜拉桥作为算例对上述分析方法进行说明.该桥桥塔为高150 m的倒“Y”型混凝土桥塔.主跨长420m.每个锚固截面的一对拉索都锚固在主梁横桥向中心位置.桥梁基本尺寸参见图5.假设结构承受桥面均布荷载作用,沿顺桥向荷载集度为50 kN·m-1.

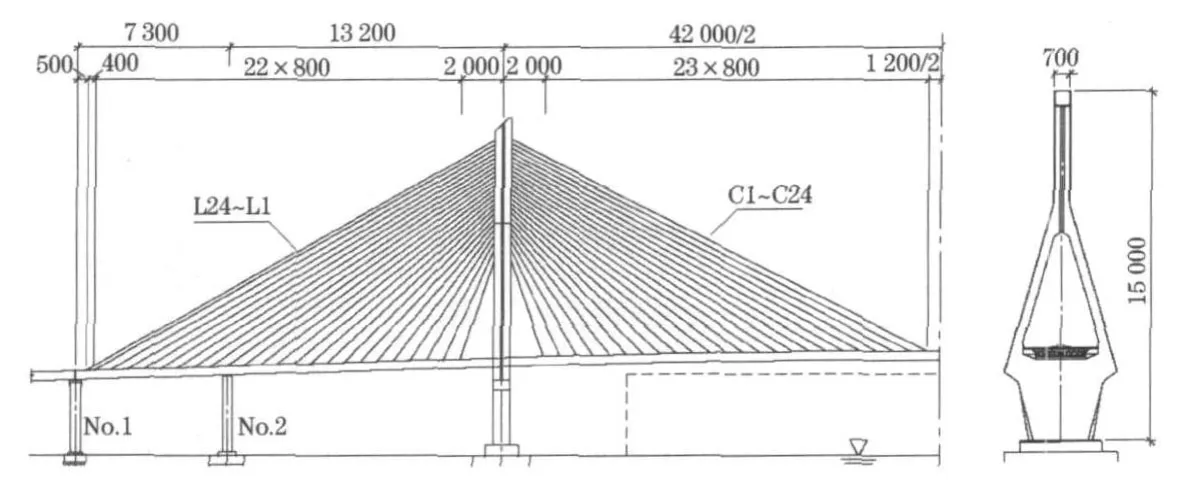
图5 斜拉桥基本尺寸(单位:cm)Fig.5 The layou t o f cab le-stayed bridge(unit:cm)

有限元模型采用的参数见表1.桥塔与主梁采用三维梁单元模拟,拉索采用空间杆单元模拟.主梁面积为2.8m2,抗弯惯性矩为4.43m4.模型中,所有质量点集中在主梁单元,采用了无质量刚性横梁来连接拉索与主梁.塔底部采用固结约束,辅助墩采用施加竖向约束来模拟.主梁上同一锚固截面的两根斜拉索由于都锚固在主梁中间位置,距离较近,在极端事件中,容易同时发生破坏,因此将一对拉索编为同一个编号,拉索及主梁节段编号见图6,拉索面积见表2.结构完好状态下,主梁的最大应力为59.08 MPa,出现在梁塔交接处的26号单元以及另一半桥梁中与其对称的主梁单元,若以210 MPa作为钢材应力限制值,则主梁最大应力安全系数μ=210/59.08=3.6.主梁的屈曲安全系数随主梁位置的变化如图7所示,其中最小屈曲安全系数λ=19.4出现在塔梁交接处的主梁单元,即与L1拉索相连的25号主梁单元以及另一半桥梁中与其对称的主梁单元.

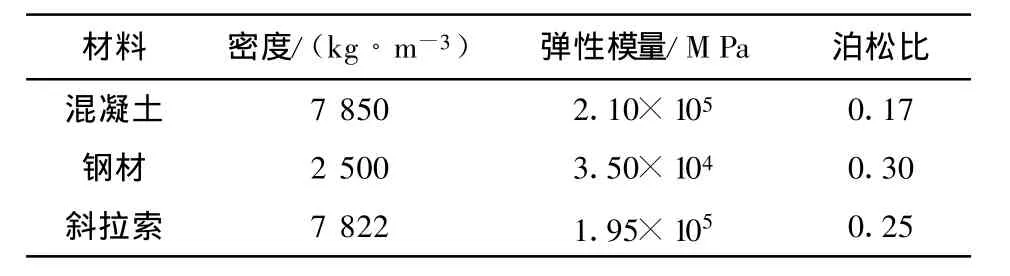
表1 材料特性表Tab.1 Material p roperties

图6 拉索及主梁节段编号示意图Fig.6 Num bering of cables and girder segmen ts

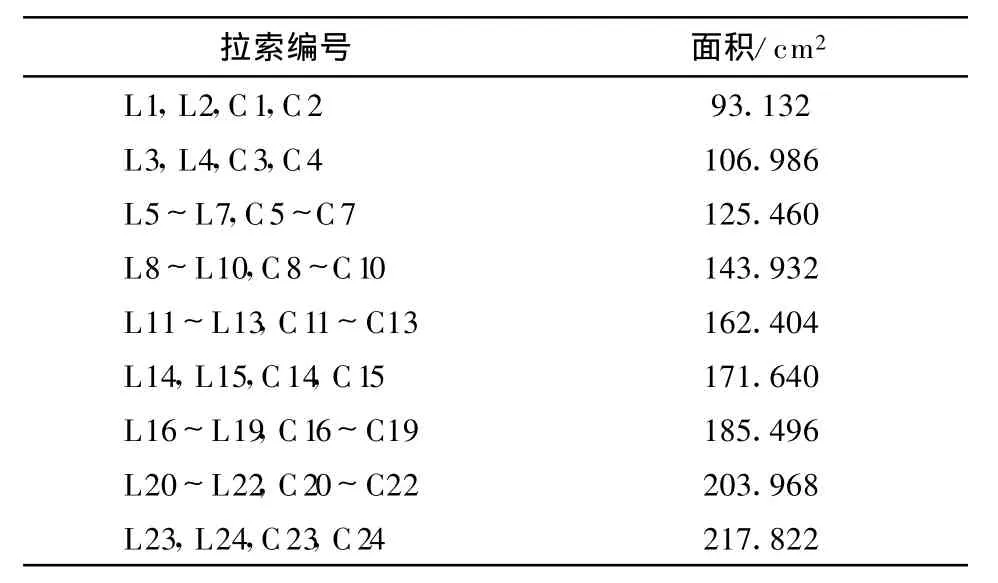
表2 斜拉索截面面积Tab.2 Cross sectiona l area o f cables

图7 完好结构主梁屈曲安全系数Fig.7 Bu ck ling safety factors of intact structu res

3.2 斜拉索损伤场景易损性分析

在极端破坏事件中,拉索的破断情况可能有很多种,本文仅从单个车辆撞击导致的拉索断裂角度对损伤场景进行假定.算例中,主梁纵向两拉索锚固点间距为8 m,因此16 m范围内是比较合理的车辆撞击范围,因此作为方法说明性算例,仅针对单对拉索的断索损伤场景进行了分析.另外,考虑到拉索极端事件中的突然破断对结构的冲击作用,在进行拟静力分析[13]时,本算例采用动力放大系数为2来近似考虑这种动力效应.

单对拉索破断损伤场景对主梁屈曲安全系数λ和最大应力安全系数μ的影响如图8所示.根据式(3)和式(4)可以得到分别以主梁屈曲安全系数和最大应力安全系数表示的各个损伤场景结构性能影响程度参数C和占结构体系总体规模的比例M.再根据式(6)得到的函数值,可以得到图9所示分别以主梁最小屈曲安全系数λ和最大应力安全系数μ为性能参数的易损场景优化选取结果.从图9a中可以看出,以主梁最小屈曲安全系数λ为结构性能参数的易损场景分别为L1,C7,C9和C12拉索的破断;图9b中以最大应力安全系数为性能参数的易损场景为C1拉索的断裂.

3.3 对计算结果的进一步讨论

从易损性分析方法以及算例分析可以看出,最终的易损场景是损伤场景在对结构性能的影响程度C和占结构体系总体规模比例M之间权衡的结果,易损性目的就是要找出C尽可能大,而M尽可能小的易损场景,而这两个要求往往很难在同一个损伤场景中实现,因此产生了帕罗托边界的概念,无论是单以C或M进行衡量,还是以两个参数占不同权重进行两参数衡量,易损场景必然落在此边界上,正如算例分析结果所示.图9b中以最大应力安全系数为参数的易损性评价得到了唯一易损场景属于比较理想的情况.对图9a以中最小屈曲安全系数为参数的易损性评价得到了帕罗托边界上的几个易损场景,若能规定两个参数的权重,则可以得到唯一的易损场景,比如只以损伤场景的破坏后果作为评价,则C12为最易损场景;若单以损伤场景占结构体系比例来评价(物理意义为发生损伤的难易程度),则L1为最易损场景.

图8 主梁屈曲安全系数及最大应力安全系数随损伤场景的变化Fig.8 Buck ling safety factor and m aximum stress o f girder to different dam age scenarios

图9 断索易损场景Fig.9 Vu lnerable scenarios of cable failu re

4 结论

本文提出了从损伤场景对结构性能的影响程度C和损伤场景占结构体系总体规模的比例M(实质上反映了损伤场景发生的难易程度)两个参数进行结构易损性评价的方法.并以主梁最小屈曲安全系数λ和最大应力安全系数μ为结构性能参数,对斜拉桥断索损伤场景进行了易损性分析.通过易损性分析,可以从众多拉索中,找出结构对其发生破断后易损性较高的拉索,从而可以为健康检测系统传感器布置提供明确参考.

本文针对拉索破断分别采用了主梁最小屈曲安全系数λ和最大应力安全系数μ两个参数进行分析,从分析结果可以看出,分析用结构性能参数不同,易损性分析结果不同.

作为结构易损性分析理念在斜拉桥结构分析中应用的说明,本文仅考虑了单个车辆撞击事故下单对拉索破断的损伤场景.极端事件下可能发生多跟拉索同时破断,要视具体破坏事件而定,而分析方法并无实质不同.

[1] Agarwal J,Block ley D,Woodman N.Vu lnerability of 3-dimensional trusses[J].Structu ral Safety,2001,23(3):203.

[2] Agarwal J,Block ley D,W oodm an N.Vulnerability of stru ctural system s[J].Structu ral Safety,2003,25(3):263.

[3] Pinto JT,Block ley D I,Woodman N J.The risk of vulnerable failure[J].Structu ral Safety,2002,24(2/4):107.

[4] 刘西拉.结构工程学科的进展与前景[M].北京:中国建筑工业出版社,2007.LIU Xila.The developm ent and prospect of structu ral engineering[M].Beijing:China A rchitectu re &Building Press,2007.

[5] 柳承茂,刘西拉.基于刚度的构件重要性评估及其与冗余度的关系[J].上海交通大学学报,2005,39(5):746.LIU Chengmao,LIU Xila.Stiffness-based evaluation of com ponent importance and its relationship w ith redundancy[M].Journal of Shanghai Jiaotong University,2005,39(5):746.

[6] 邱德锋,周艳,刘西拉.突发事故中结构易损性的研究[J].四川建筑科学研究,2005,31(2):55.QIU Defeng,ZHOU Yan,LIU Xila.Study on the structu ral vulnerability under unexpected conditions[J].Sichuan Building Science,2005,31(2):55.

[7] Liu C M,Liu X L.Structural vulnerability analysis of th ree dimensional truss[C]∥IABSE Symposium on Structures and Ex treme Events.Lisbon:ETH Honggerberg,2005:1-8.

[8] Yu G,Sun Z,Sun L M.Vulnerable com ponent monitoring:a novel concept for health m onitoring of complex structu res[C/CD]∥Structu ral Health M onitoring & Intelligent Infrastructure.Vancouver:ISISCanada Corporation,2007.

[9] Yu G,Sun Z,Sun L M.Structu ral vulnerability analy sis for capacity assessment and enhancement of truss bridges[C/CD]∥The 10th InternationalConference on Structu ral Safety and Reliability.Osaka:CRC Press Taylor&FrancisG roup,2009.

[10] 贡金鑫,魏巍巍.工程结构可靠性设计原理[M].北京:机械工业出版社,2007.GONG Jinxin,W EI Weiw ei.Reliability design theory of engineering structures[M].Beijing:China M achine Press,2007.

[11] 林辉,陈艾荣.基于恐怖袭击的桥梁设计[J].世界桥梁,2009(2):17.LIN Hui,CHEN A irong.Design of bridge on terrorist attacks[J].W orld Bridges,2009(2):17.

[12] 李国豪,项海帆,沈祖炎,等.桥梁结构稳定与振动[M].北京:中国铁道出版社,2002.LIGuohao,X IANG H aifan,SHEN Zuyan,et al.S
Tability and vib ration of b ridge structu res[M].Beijing:China Railw ay Publishing H ouse,2002.

[13] Ruiz-Teran A M,Aparicio A C.Dynam ic amplification factors in cable-stayed stru ctures[J].Journal of Sound and V ibration,2007,300(2007):197.