围岩不同模量特性对隧道支护结构的影响分析

杨 钊,余 俊,潘晓明,王艳丽

(1.同济大学地下建筑与工程系,上海200092;2.同济大学岩土及地下工程教育部重点实验室,上海200092)

大量的实验和研究表明,材料在绝对值相同的单轴拉应力或压应力作用下,会发生绝对值不同的拉应变和压应变,即材料具有受拉、压不同弹性模量的非线性特性.实际上,土木工程中广泛应用的岩材、砖材、混凝土、有机玻璃、塑料等存在显著的拉、压不同模量的力学属性.但在目前的工程设计与施工中,并没有考虑到材料的这一属性,这将有可能造成较大的设计误差,成为结构失效的隐患[1-2].因此,开展拉压不同模量弹性理论的研究,不仅有重要的理论意义,也有广泛的工程应用空间.

拉压不同模量理论是20世纪60年代由前苏联学者阿姆巴尔楚扬提出,并给出了圆柱壳轴对称不同模量问题的解析解,随后国内外学者针对实际工程问题导出了圆柱弯曲、柱形孔扩张问题、弯压柱、横力弯曲梁、挡土墙等的解析解,针对复杂问题,解析解无法得到,有限单元法被应用于求解材料拉压不同模量问题[3-6].

洞室开挖后,支护结构的受力与变形与围岩的物理力学性质密切相关.国内外众多学者研究了围岩的弹塑性、各向异性以及蠕变性质对支护结构的受力和变形影响[7-10],但针对围岩拉压不同模量特性对支护结构的影响研究还较少.

山岭隧道围岩具有典型的拉压不同模量的属性,以下将讨论在弹性参数变化情况下,这一属性对支护结构的受力和变形的影响,为隧道支护结构设计提供新的理论依据.

1 不同模量材料弹性本构关系

1.1 主应力方向本构关系

不同模量弹性力学是建立在经典的各向同性弹性力学基础上,两者的平衡方程与几何方程完全相同,本构方程均依据广义胡克定律定义.但二者的区别在于本构关系中的弹性常数取值的差异.不同模量弹性本构方程根据一点的主应力的拉、压状态选取弹性常数(受拉时取弹性模量为E+、泊松比为ν+,受压时取弹性模量为E-、泊松比为ν-),而经典的各向同性弹性本构方程的弹性常数与受力状态无关(E+=E-,ν+=ν-).由广义胡克定律,拉压不同模量弹性力学本构方程在主应力方向可以写为

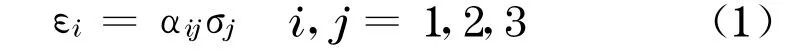
式中:εi为主应变;σj为主应力;αij=-ν+/E+(或-ν-/E-),i≠j;当σi＞0 时 ,αii=1/E+;当 σi＜0时 ,αii=1/E-.

1.2 笛卡尔坐标系下本构关系

设3个主应力方向在笛卡尔坐标系下的方向余弦如表1所示

表1 主应力方向余弦Tab.1 Direction cosine of principal stress

在笛卡尔坐标系下,单元主应变可由全应变利用坐标转轴公式得到

式中

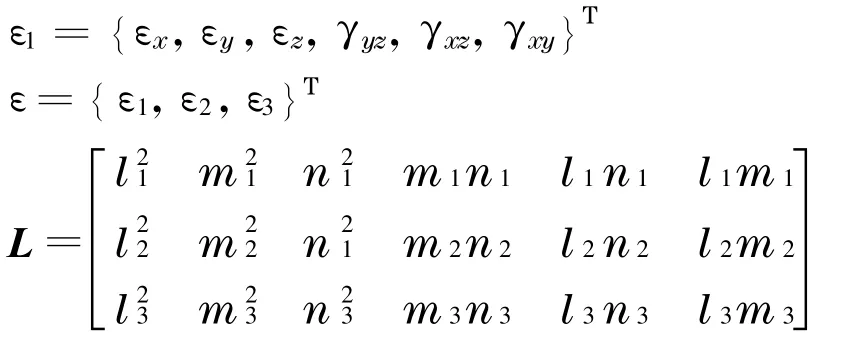
基于主应变的单位体积应变能为

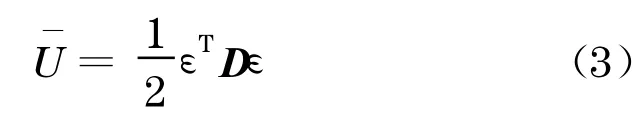
基于全应变的单位体积应变能为

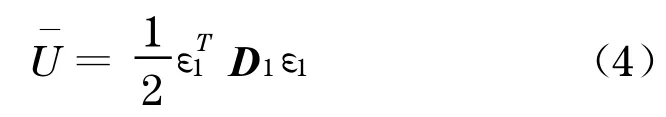
由单位体积应变能相等可得

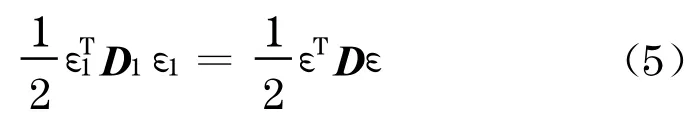
将式(2)代入式(5)可得

笛卡尔坐标系下不同模量弹性本构关系为

2 不同模量弹性力学有限元单元法

2.1 不同模量弹性力学有限元计算方法

在非线性有限元计算中,常采用迭代法和增量法求解.增量法求解是用直线拟和曲线的过程,需用较小的荷载增量才能得到比较精确的解.迭代法是通过多次迭代,逐步调整材料的状态参数,使得材料满足非线性本构方程.考虑到计算的经济性,本文拟采用迭代法求解不同模量弹性力学问题.

在迭代法求解中,牛顿法收敛最快,但采用牛顿法计算需要用到材料的切线本构矩阵,又由式(7)可知,不同模量弹性本构矩阵为割线本构矩阵,因此,在计算中拟采用初应力法和直接迭代法,但因直接迭代法对凸函数求解不收敛并且在每一个计算步都要求解刚度矩阵的逆[11],使得计算不经济.因此选用初应力法求解不同模量弹性力学问题.

2.2 拉压不同模量弹性力学有限元迭代格式

有限单元法表示的平衡方程[12]为

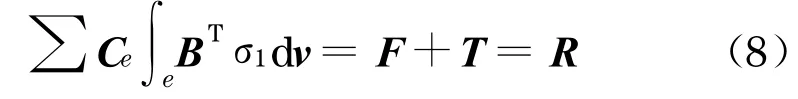
式中:Ce为选择矩阵;B为应变矩阵;F=∑CeFe,为整个系统的体力荷载矢量,Fe为单元的体力荷载矢量;T=∑CeTe,为整个系统的面力荷载矢量,Te为单元的面力荷载矢量;R为整个系统的荷载矢量.

将式(7)改写成

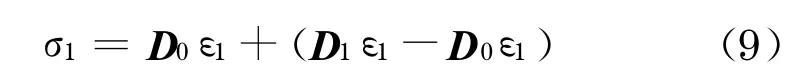
代入式(8)得

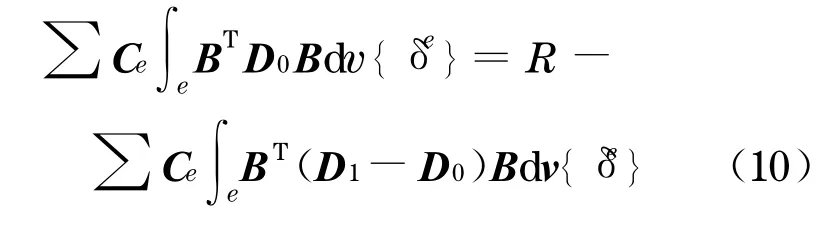
式中:D0为初始给定的本构矩阵,在本次计算中,为了使收敛速度较快,取为受压的经典弹性本构矩阵;{}为有限元节点位移向量.

由式(10)可以建立一种迭代求解格式

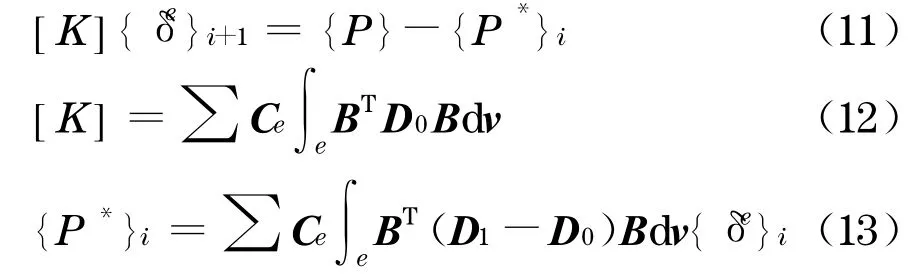
式中:i代表迭代序列.

整个求解过程如下[13]:

(1)设定常刚度矩阵[D 0].

(2)由第i步迭代步的应力状态和给定的常刚度矩阵,按公式(11)求解{δe}i+1,并根据节点的位移状态计算节点的应力状态.

二维状态下由位移场计算应力场的方法(三维状态下类似)如下:

(1)由节点位移计算节点应变.

(2)假设节点应力状态处于第一类区域双向受压,用受压型本构关系(经典弹性本构)计算节点应力状态,并求解节点主应力.如果主应力均小于零,则此假设成立,否则进入下一步判断.

(3)假设节点应力状态处于第一类区域双向受拉,用受拉型本构关系(经典弹性本构)计算节点的应力状态,并计算节点的主应力.如果主应力均大于零,则此假设成立,否则进入下一步判断.

(4)判断节点剪应变是否为零,如果剪应变为零,根据x轴和y轴的应变状态来判断出节点的本构关系(此时应变的拉、压状态即为应力的拉、压状态),计算应力,否则进入下一步判断.

(5)根据节点应变计算节点的主应变和转换矩阵,此时最大主应变为拉应变,根据主应变方向上的本构关系求得整体坐标系下的本构关系,然后计算节点应力.

2.3 拉压不同模量弹性力学有限元程序验证

考虑一个平面应力圆环,内半径为a,外半径为b,圆环内受均匀内压p.圆环内环向应力σθ为拉,径向应力σr为压.圆环应力解析解为[14]

有限元程序验证中,取圆环内半径a=1 m,圆环外半径b=2 m,圆环内压p=60 kPa,笛卡尔坐标系原点位与圆环圆心重合.圆环弹性常数设为:E-=1.0×1010Pa,ν-=0.3,E+=0.5×1010Pa,ν+=0.15.

圆环主应力等值线与圆环边界线组成一组同心圆弧,如图1所示.有限元计算结果与解析解计算结果对比见表2,环向应力最高误差为0.93%,平均相对误差为0.64%;径向应力最高误差为2.13%,平均误差为1.17%.该误差源于有限元数值计算中网格的划分,迭代收敛判断准则以及其他诸多综合因素的影响.由此可见,编制的有限元程序是可靠的,可用于实际工程计算.

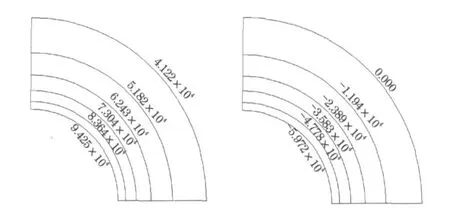
图1 圆环主应力等值线示意图(单位:Pa)Fig.1 Contou r map of princ ipa l stress(unit:Pa)

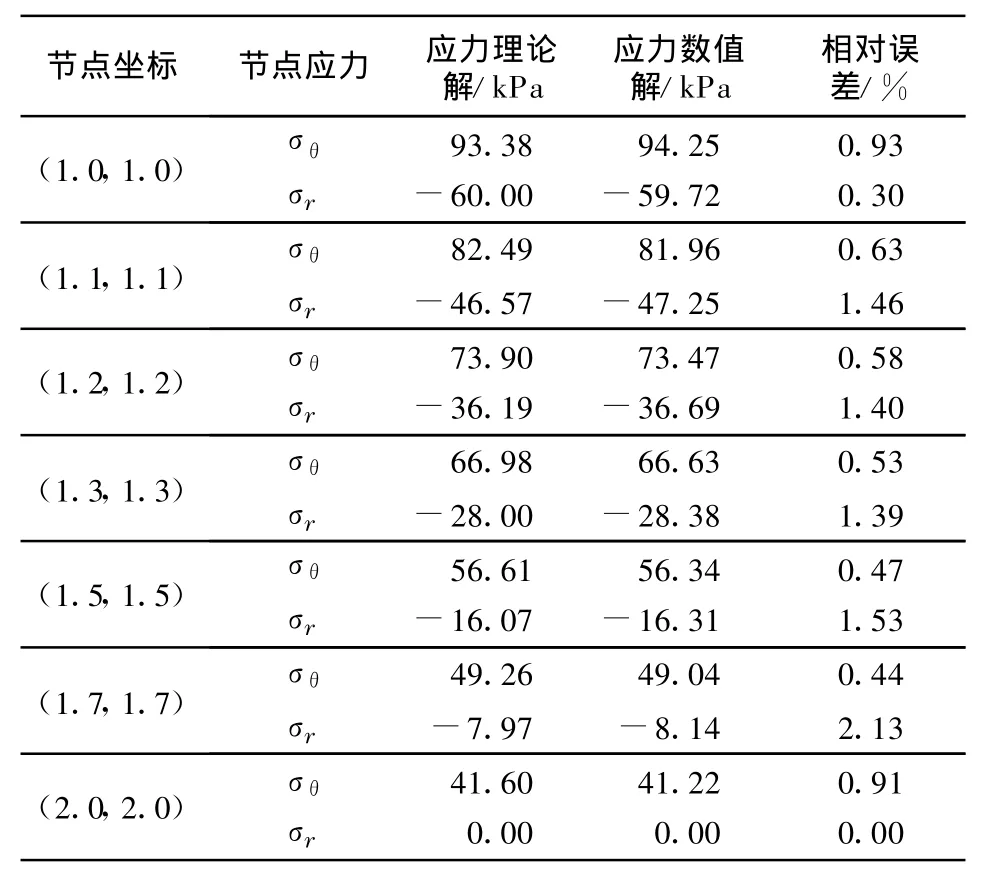
表2 理论解与数值解对比Tab.2 Com parison of theory so lution an d numer ica l so lution

3 隧道模型、参数和有限元实现

3.1 隧道模型

隧道纵向结构可以认为是一无限长的结构体,在不考虑隧道结构纵向变形的影响,以及在隧道地表起伏不大的区域,可将隧道结构的变形与受力简化为平面应变问题.文中目的是为了讨论初期支护结构在考虑围岩拉压不同模量性质下的受力与变形,并不考虑围岩与初期支护结构的强度与破坏问题,因此将围岩与初期支护结构均视为弹性体.

选取隧道典型断面,隧道断面为R=12.00 m,R=6.15 m和R=2.50 m的三心圆形式.隧道洞跨12.30 m,洞高9.46 m,根据洞室开挖对围岩的影响范围,有限元分析范围水平向取5倍的洞跨;竖向从隧道底部向下取20m.

3.2 有限元实现

有限元网格如图2所示.围岩与初喷混凝土支护采用8节点的平面应变单元.锚杆采用桁架单元模拟,锚杆单元采用嵌入单元技术嵌入围岩中.隧道的开挖、初期支护的施作均采用“生死”单元技术,隧道开挖单元先“生”后“死”,初期支护单元先“死”后“生”.单元的“生”、“死”通过调整单元的刚度矩阵变化来实现.单元“生”状态,单元的刚度矩阵由给定单元的D矩阵形成;单元“死”状态,单元刚度矩阵等于单元“生”状态刚度矩阵乘无穷小系数.

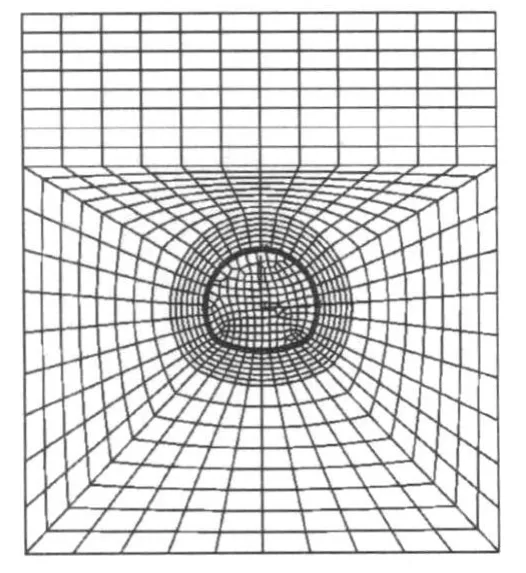
图2 有限元计算网格Fig.2 Mesh of finite elem entm ethod

在模拟洞室开挖之前,要对岩体进行初始地应力场平衡.在有限单元程序中,岩体的初始地应力场平衡分为两步实现.第一步:施加自重荷载,输出节点内力;第二步:重新计算,施加自重荷载和节点内力,平衡初始地应力场.第二步分为2个时间步实现:

(1)施加自重荷载,计算岩体的应力场与位移场,此时间步1计算所得的应力场即为初始平衡状态下的应力场.

(2)将第一步所得节点内力作为外荷载施加在节点上,并计算此时位移场,此时间步位移场计算结果趋近于零,即为初始平衡位移场.强制设定第2个时间步的应变增量为零,则第2个时间步应力增量也为零.第2个时间步末岩体的状态即为初始地应力平衡状态.

3.3 地层、支护参数

为了突出拉、压不同模量系数对支护结构内力和变形的影响,将隧道结构周围围岩看作均质的.取围岩的弹性参数为

主应力坐标轴下平面应变的本构方程为

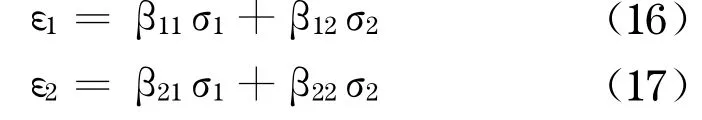
当σ1,σ2 同号时 ,为经典的弹性本构 .当 σ1,σ2 异号 ,且 σz＞0 时,β11=(1-ν+2)/E+,β12=β21=-ν+(1+ν+)/E+,β22=1/E--ν+2/E+.当 σ1,σ2异号,且 σz＜0 时 ,β11=1/E+-ν-2/E-,β12=β21=-ν-(1+ν-)/E-,β22=(1-ν-2)/E-.

锚杆采用 Φ5 mm的砂浆锚杆,弹性模量E=2.0×105MPa,泊松比ν=0.3.

初期支护采用钢拱架,挂钢筋网(Φ8 mm,20@20)、喷C25混凝土厚250 mm,材料参数按照《公路隧道设计规范》选取,见表3[15].

表3 喷射混凝土物理力学性质Tab.3 Physicalandmechanical parameters of shotcrete

4 有限元计算结果分析

不同模量计算理论与经典的弹性理论计算结果的差异,主要与不同模量系数α=E+/E-有关.针对不同的不同模量系数α,分析在相同荷载条件下,锚杆轴力和初砌结构应力场与位移场的响应.

当α从0.4变化到3.0时,衬砌结构的最大位移量变化小于10%,变化并不是很明显,如图3所示.这主要因为对于隧道断面,衬砌结构最大位移处垂直方向的位移远大于水平方向的位移,整个计算区域受压区远大于受拉区,且受拉主应力方向主要集中在洞顶、洞底两侧的水平区域,对垂直方向位移影响较小.如果当泊松比较小时,围岩与衬砌结构受拉区区域增大,α对洞顶衬砌结构的位移影响也将增大.

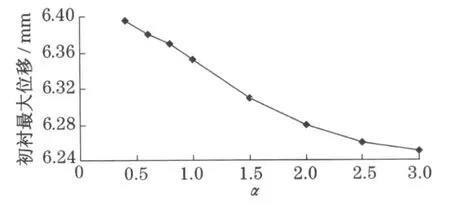
图3 衬砌最大位移与α关系曲线Fig.3 Maxim um disp lacem ent of linear variationsw ithα

当α从0.4变化到3.0时,锚杆轴力变化在5%范围以内,变化并不明显,如图4所示.这是因为采用嵌入单元技术后,锚杆的受力大小主要与隧道周边围岩位移场变化相关,可以不计围岩不同模量属性对锚杆轴力的影响.

图4 洞顶锚杆最大轴力与α关系曲线Fig.4 M aximum axia l force o f anchor var iations w ithα

采用不同模量有限元程序计算后可知,随着不同模量系数α的增大,衬砌结构最大主应力值增大,受拉区区域也变大,如图5所示.当α从0.4变化到3.0,最大主应力值的变化幅度超过30%(均相对于经典的弹性理论解),如图6所示.如果当围岩的泊松比更小(从经典弹性力学可知,此时围岩和初期支护受拉区的区域更大),则最大主应力值随 α的变化将更加明显.需要注意的是,当 α取不同值时,最小主应力值的变化却不超过1%,如图7所示,且位置并没有发生改变,均位于隧道断面的侧面.因此可以认为围岩不同模量属性对衬砌结构最小主应力不造成任何影响.

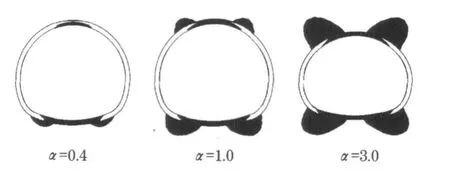
图5 衬砌与围岩受拉区Fig.5 Tensile zone o f linear and surrounding rock

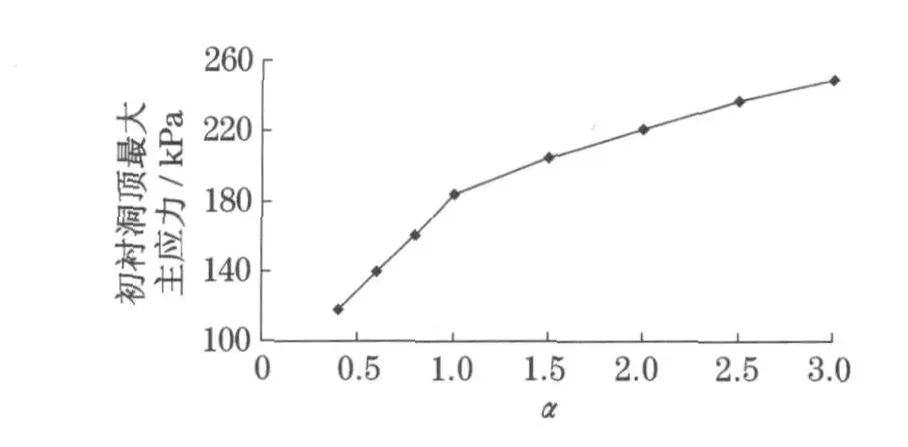
图6 衬砌洞顶最大主应力与α关系曲线Fig.6 Maximum princ ipa l stress variations at arch vau lt o f linear w ithα

5 结论

岩石这样的脆性材料,具有明显的拉压不同模量属性,如果仍沿用经典弹性理论进行设计,将可能带来显著的误差.本文考虑了隧道的自重应力场、隧道的开挖与隧道初期支护的施作,分析了隧道围岩的不同模量特性对衬砌结构受力与变形的影响,得出了以下结论:

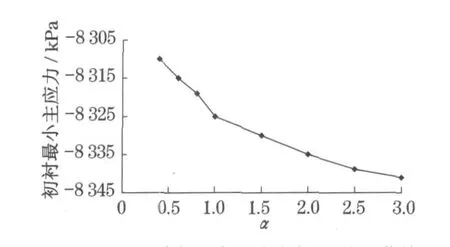
图7 衬砌最小主应力与α关系曲线Fig.7 M inimum pr incipal stress o f linear variation s withα

(1)围岩的受压弹性泊松比较小时,采用经典弹性理论计算所得的受拉区较大,围岩的不同模量属性对支护结构的位移场与应力场影响增大.

(2)对于不同模量系数较大的围岩,应在隧道洞顶适量加大钢筋网的密度,以防止初砌脱落或隧道坍塌等事故发生.

(3)对于不同模量系数较大的围岩,应在隧道洞顶适当加长锚杆锚固长度,防止围岩因受拉破坏而失稳.

(4)围岩不同模量系数的变化,对锚杆轴力和衬砌结构变形影响较小,在工程设计中可按经典弹性理论计算锚杆轴力与衬砌结构变形量.

(5)隧道结构在地应力场的作用下,围岩与衬砌结构绝大部分位于受压区,因而围岩不同模量系数的变化,对衬砌结构受拉区应力场有显著的影响,而对衬砌结构的受压区应力场影响微小.

[1] 何晓婷.拉压不同模量弹性结构的非线性力学行为研究[D].重庆:重庆大学土木工程学院,2007.HE Xiaoting.Study on nonlinear mechanics behavior of elastic structure with different tension and compression moduli[D].Chongqing:Chongqing University.College of CivilEngineering,2007.

[2] 阿姆巴尔楚米扬C A.不同模量弹性理论[M].邬瑞锋,张允真,译.北京:中国铁道出版社,1986.Ambartsumyan C A.Elasticity theory of different modulus[M].Translated by WU Ruifeng,ZHANG Yunzhen.Beijing:China Railw ay Press,1986.

[3] 姚文娟,叶志明.不同模量横力弯压柱的解析解[J].应用数学与力学,2004,25(9):236.YAOW en juan,YE Zhim ing.Analytical solu tion of bendingcom pression colum n using different tension-comp ression moduli[J].Applied Mathematics and Mechanics,2004,25(9):236.

[4] 杨海天,朱应利.光滑函数求解拉压不同弹性模量问题[J].计算力学学报,2006,23(1):19.YANG Haitian,ZHU Y ingli.Solving elasticity problems with bi-modulus via a smoothing technique[J].Chinese Jou rnal of Compu tationalM echanics,2006,23(1):19.

[5] Papazoglou J L,Tsouvalis N G.Mechanical behaviors of bim odu lus lam inated plates[J].Com posite Structures,1991,17(1):1.

[6] Srinivasan R S,Ramachandra L S.Large deflection analysis of bi-modulus annu lar and circular plates using finite elemen ts[J].Com putes&Stru ctures,1989,31(5):681.

[7] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.SUN Jun.The rheological property of geotechnical material and engineering application[M].Beijing:China A rchitectu re&Building Press,1999.

[8] 许建聪.浅埋风化岩质隧道初支护后黏弹性变形性态分析[J].岩石力学与工程学报,2007,26(9):1781.XU Jiancong.Analysis of visco-elastic deformation behavior of shallow buried decom posed-rock tunnel after prelim inary support[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(1):1781.

[9] 黄宏伟,徐凌.大风垭口岩石公路隧道围岩及初期支护变形与内力研究[J].岩石力学与工程学报,2004,23(1):44.HUANG Hongw ei,XU Ling.Study on deformation and in ternal force of supporting rock sand initialsupport in Dafeng-Yakou rock road tunnel[J].Chinese Jou rnal of Rock Mechanicsand Engineering,2004,23(1):44.

[10] 张学民.岩石材料各向异性特征及其对隧道围岩稳定性影响分析[D].长沙:中南大学土木建筑学院,2007.ZH ANG Xuem in.Anisotropic characteristic of rock m aterial and its effect on s
Tability of tunnel surrounding rock[D].Changsha:Cen tral Sou th University.School of Civil Engineering and A rchitectu re,2007.

[11] 朱伯芳.有限单元法原理与应用[M].北京:中国水利水电出版社,2004.ZHU Bofang.The finite elem ent method theory and application[M].Beijing:ChinaW aterPower Press,2004.

[12] 王勖成.有限单元法[M].北京:清华大学出版社,2006.WANG Xucheng.The finite element m ethod[M].Beijing:Tsinghua University Press,2006.

[13] 杨钊,王渭明,吴克新.围岩不同模量特性对巷道围岩应力和变形的影响研究[J].山东科技大学学报,2008,27(1):1.YANG Zhao,WANG Weim ing,WU Kexin.Research on the effect of different m odulus characteristic of the surrounding rock to the stress and defo rm ation of roadway tunnel[J].Jou rnal of Shangdong University of Science and Technology,2008,27(1):1.

[14] 陈子荫.围岩力学中的解析方法[M].北京:煤炭工业出版社,1994.CH ENG Ziyin.The analytic method of su rrounding rock mechanics[M].Beijing:China Coal Industry Pub lishing H ouse,1994.

[15] 中华人民共和国交通部.TJGD 370-2004公路隧道设计规范[S].北京:人民交通出版社,2004.M inistry of Communications of People's Republic of China.TJGD370-2004 Design code of high road tunnel[S].Beijing:China Communications Press,2004.