地应力对脆性岩体洞群稳定性的影响

刘立鹏，姚磊华，王成虎，何朋朋

(1. 中国地质大学 工程技术学院，北京，100083；2. 中国地震局 地壳应力研究所，北京，100085)

随着社会的发展及建设的需求量日益增大，地下构筑物及采矿工程等逐渐向地表深处延伸。随着埋深增加，地应力对工程体稳定性的影响愈明显。在地应力较低时，视岩体完整程度，围岩分别表现出弹性响应、块体滑移和散体型破坏。而在地应力较高时，地应力对洞室围岩稳定起主导作用。在高地应力作用下，脆性岩体积聚大量弹性应变能，开挖临空面释放应力，易于发生脆性破坏，严重时发生大范围急剧岩爆地质灾害，其破坏形式既包括弹性应变能突然释放的突然脆性破裂如岩爆，也包含其他形式的静态破坏如葱状剥落等[1]。关于洞室围岩的脆性破坏，谢兴华等[2-5]进行了相关研究。但目前的研究多集中于脆性破坏的方式及其是否发生预测上[6-8]，而对脆性破坏的深度范围研究较少，且未将初始地应力场特征与脆性破坏深度范围及形状的变化结合起来。此外，地下洞室形状及洞群间距均对围岩脆性破坏深度产生较大影响。为此，在影响洞室围岩脆性破坏深度的各不同因素下，本文作者首先对破坏深度特征如初始地应力场特征、洞室间距、洞室形状及岩石单轴抗压强度等进行对比分析；其次，对中国大陆地应力分布规律进行分析；最后，分析不同种类围岩在中国大陆地应力分布规律下，随初始应力场的变化、围岩脆性破坏深度演化规律，并与实际工程破坏特征进行对比分析。

1 洞群脆性破坏影响因素

脆性围岩积聚大量弹性应变能，在开挖卸荷条件下易发生脆性破坏。在地下洞室群建设中，开挖洞室围岩应力路径不同将对洞室围岩稳定性产生不同影响，且在不同地应力组合及洞室形状下，脆性破坏形式及范围将发生变化(图1)。岩石脆性系数不同，则积聚弹性应变能不同。研究不同初始应力场作用下，不同洞室形状、洞群间距及岩石单轴抗压强度对洞室围岩脆性破坏的影响十分必要。

Martin等[4-5,9]对围岩脆性破坏进行了研究，其中，基于弹性模型的m-0准则应用较广泛。此准则考虑了地应力作用及岩体强度特性与岩石强度特性之间的不同，并认为岩体发生脆性破坏，主要是黏聚力丢失所致，摩擦角在脆性破坏时并未被激发，其作用可被忽略。该准则是在 Hoek-Brown强度准则的基础上，将参数m视为0，s=1/3[5]，即

式中：σ1和σ3为最大、最小主应力；σc为岩石单轴抗压强度。利用m-0脆性破坏准则结合 Examine2D[10]弹性分析软件，对不同地应力特征及洞室形状下的围岩脆性破坏深度进行对比分析。不同主应力时复合强度包络线见图1[4]。

图1 主应力不同时的复合强度包络线Fig.1 Composite strength envelope with different principal stresses

1.1 地应力

不同应力比对围岩破坏深度的影响见图2。由图2可知：围岩脆性破坏深度比与应力比，和分别为最大、最小初始地应力)近似呈直线性关系，随着应力比的增加，脆性破坏深度逐渐增大。

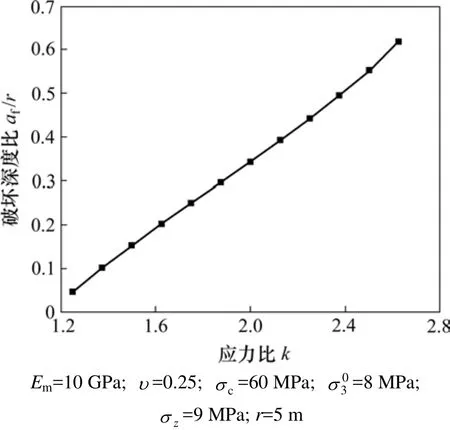
图2 应力比对破坏深度的影响Fig.2 Effect of principal stress ratios on depth of brittle failure

应力比不同时圆形洞室脆性破坏范围见图3[4]。从图3可见：屈服及破坏范围随着应力比k的增加逐渐增大，且屈服范围偏离主应力方向，偏转角θ逐渐向45˚方向发展。

图3 不同应力比时圆形洞室脆性破坏范围Fig.3 Extent of brittle failure around a circular opening defined for various principal stress ratios k

主应力偏转时屈服范围见图4。从图4可见：单洞室屈服及脆性破坏范围呈轴对称形式垂直于最大主应力方向；当多洞室平行排列时，脆性破坏及屈服范围随着主应力偏转而偏转，洞室间呈点对称形式，且单洞内破坏及屈服范围宽度、深度不等，呈非轴对称形式；随着应力比增加，屈服范围逐渐靠拢并合并；当最大主应力方向与洞室连线呈 45˚时，屈服范围最易于相互合并。

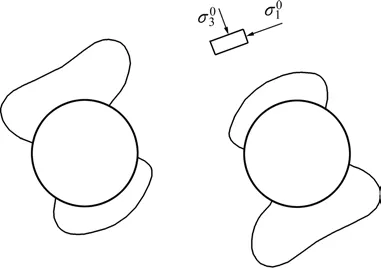
图4 主应力偏转时平行双洞室的屈服范围Fig.4 Extent of yield around two parallel openings with deflection of principal stress

1.2 洞室间距

洞室开挖对已有洞室不同部位、围岩应力产生不同影响，如应力变化及主应力方向发生旋转等，进而对洞室围岩稳定性产生不同影响。本文作者对圆形双洞室不同间距下脆性破坏深度范围进行模拟分析，所得结果见图5。

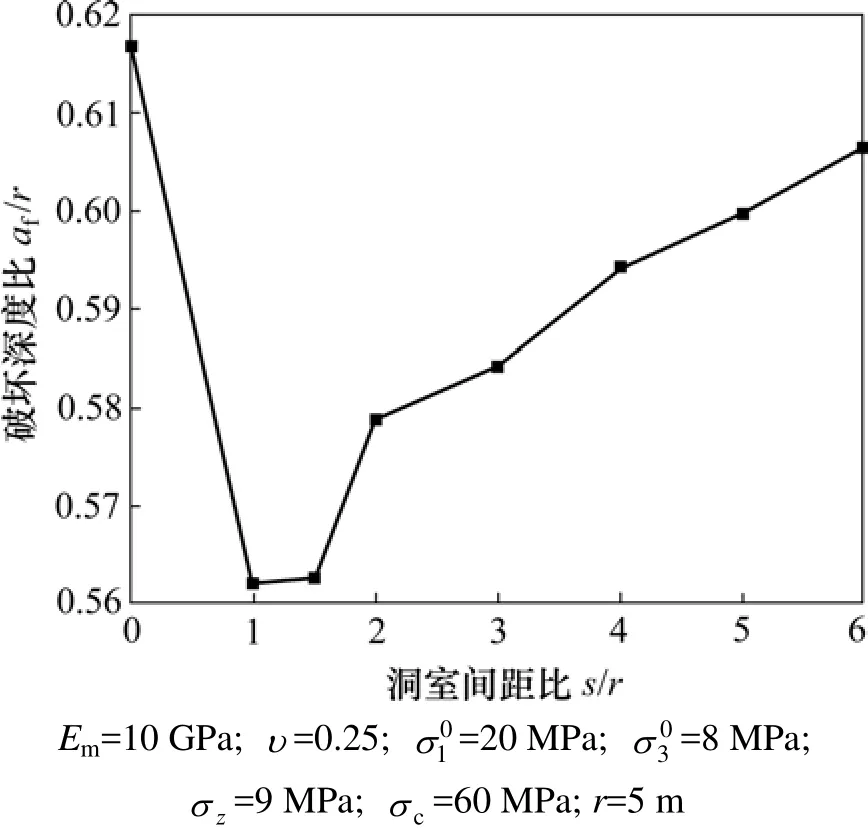
图5 洞室间距对破坏深度的影响Fig.5 Effect of spacing on depth of brittle failure

由图5可知：随着洞室间距增加，脆性破坏深度逐渐增加，并逐渐与单洞室破坏深度接近；当洞室间距较小时，随着应力比增加，脆性破坏范围增大，并逐渐相互结合。故当脆性围岩在应力及应力比较小时，可考虑较小间距设置洞室，但当应力较大时，不宜设置较小洞室间距。而对于软弱岩体，由于邻近洞室对已有洞室侧壁围岩应力具有恶化效应，洞室越邻近，侧壁应力释放区越大，不建议小间距设置洞室。

1.3 洞室形状

洞室形状不同，应力集中系数FSC(即(3σ1-σ3)/σc)发生相应变化(见图 6)，对应脆性破坏深度及范围亦不同。

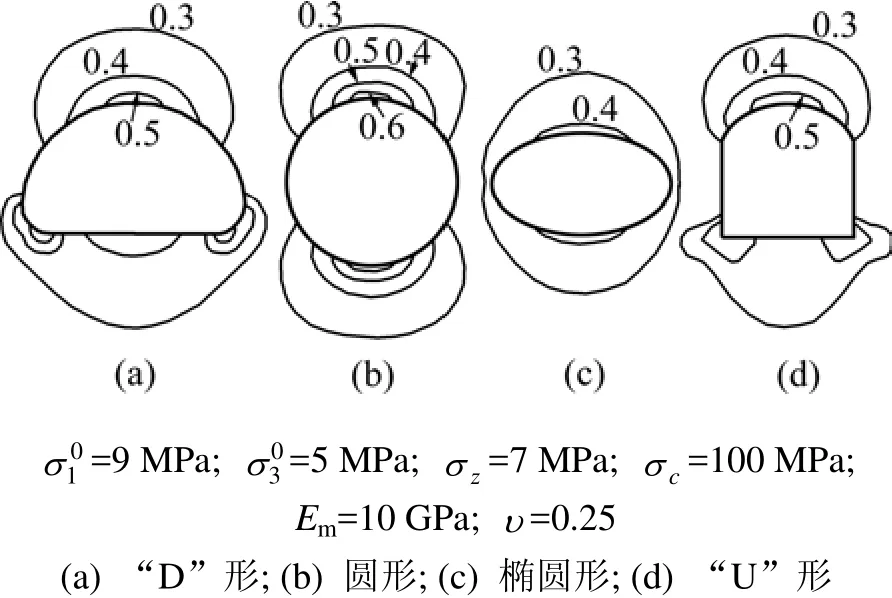
图6 不同洞形应力集中系数FSCFig.6 Stress concentration factor of different shape excavations

对比分析应力比不同时，不同形状洞室围岩脆性破坏范围后发现：不同洞形下脆性破坏深度与最大、最小主应力比k有关：当k接近于1时，圆形洞室脆性破坏深度最小；当k不为1时，若椭圆洞室长轴方向与最大主应力方向平行，则相对其他洞室深度较小；当其长、短轴长度之比与k较接近时，其破坏深度最小；“U”形及“D”形的破坏深度较小。故对于主应力相差较大时的地下工程，椭圆形洞室(谐洞)是减少围岩脆性破坏甚至降低岩爆地质灾害的最有利洞形。

1.4 岩石单轴抗压强度

初始地应力环境不同，围岩破坏表现不同响应方式：地应力较低时，围岩破坏主要为结构面控制型破坏；应力中等时，围岩破坏由地应力及结构面共同控制；地应力较高时，围岩破坏则为应力主导型破坏。本文分析高地应力环境下岩石单轴抗压强度(σc)的变化以及脆性破坏深度的发展规律，所得结果见图7。

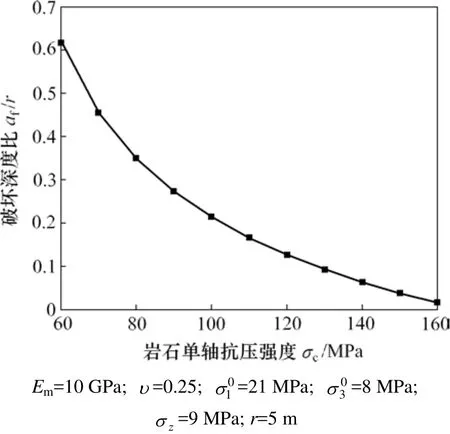
图7 岩石单轴抗压强度对破坏深度的影响Fig.7 Influence of strength on depth of brittle failure

由图7可知：随着单轴抗压强度增加，脆性破坏深度逐渐减小，两者间呈指数函数关系，并不呈线性关系。对于较完整岩体，当σc大于一定值(约等于)时，围岩不会发生脆性破坏。

2 地应力分布特征

2.1 世界地应力分布

Brown和Hoek对世界不同地区地应力测量结果进行归纳总结，得出世界各国垂直应力σv随深度H的变化规律，其拟合公式为[11]：

他们根据测量结果，对世界平均水平地应力(σH+σh)/2与垂直地应力σv之比随深度变化进行了回归分析，得出：

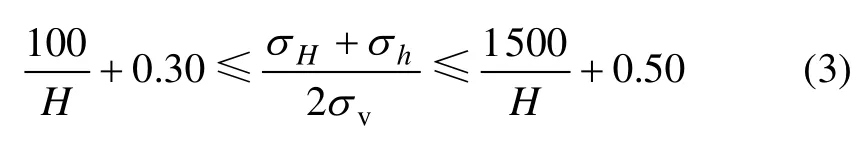
同时，朱焕春等[12]分析了全球水平地应力σH和σh，线性回归结果为：

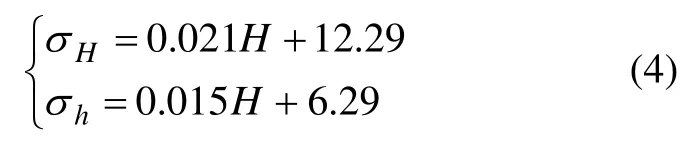
Fuchs等[13]搜集了世界各国的地应力测试数据，并生成世界应力图WSM 2000。

2.2 中国地应力分布

中国地应力总体分布特征是东低西高，且由于构造运动作用，水平应力高于垂直应力。景锋等[14]根据所收集的400多个钻孔实测地应力数据，对中国大陆地应力进行回归分析，得出垂直应力为：

这与Brown和Hoek所得结果[11]近似，但对于地形地貌起伏较大及潜蚀剥蚀作用较为强烈的区域，这两者之间存在一定的误差。对于实际工程，应参照上覆岩体密度及地形地貌情况，进行实地测量并修正。对于中国大陆，σH和σh为：

对比式(4)和(6)发现：我国地应力与世界地应力变化规律总体一致。导致两式中常数项差异较大的原因较多，如一些研究者的统计源较早[11]、欧洲地盾与中国地台不同等。

赵德安等[15]对中国平均水平地应力与垂直地应力进行分析后得：

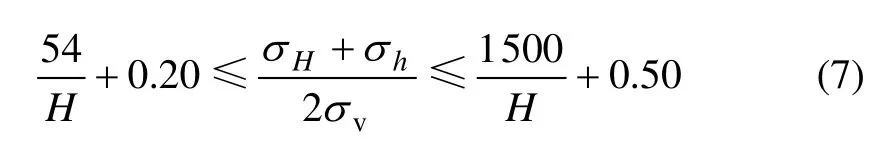
对比我国与世界统计结果发现：两者的地应力外包线一致，内包线不同；中国浅层(300 m)平均水平地应力与垂直地应力之比略小；同时，中国浅层水平应力与其他国家如加拿大、澳大利亚等的浅层水平应力相比较小。虽然近年对地应力实测较多，但多集中于较稳定工程区，构造运动较弱，进一步造成了两者的差异，且在深度在1.2 km以内，中国平均水平地应力与垂直地应力之比小于 Hoek-Brown中值曲线中的比值；而当深度大于1.2 km时，此比值比Hoek-Brown中的比值大[15]。

3 中国地应力分布下的脆性破坏规律

地壳浅部地应力受地形影响较大，随着埋深增加，可将水平主应力视为2个空间主应力，尤其是在地形平坦或埋深较深时误差会降低，并可予以忽略。本文利用中国主应力回归公式及其分布规律，以深度为变量，对沉积岩、岩浆岩及变质岩3种岩性中圆形洞室脆性破坏深度演化规律进行模拟分析。圆形洞室主应力参数见表 1，在圆形洞室中，砂岩、花岗岩和石英岩的单轴抗压强度分别为120，180和220 MPa。

表1 圆形洞室主应力Table 1 Principal stresses of circular underground openings

在中国大陆浅层应力场下，砂岩、花岗岩及石英岩洞室的脆性破坏起始埋深不同。总体趋势表明：对于脆性岩体，岩石单轴抗压强度降低，相同地，在应力环境下越容易发生脆性破坏，且破坏深度越大。不同种类围岩脆性破坏深度变化见图8。从图8可知：对于不同种类围岩，其破坏深度增加幅度不同，单轴抗压强度越高，脆性破坏深度增加比越小。

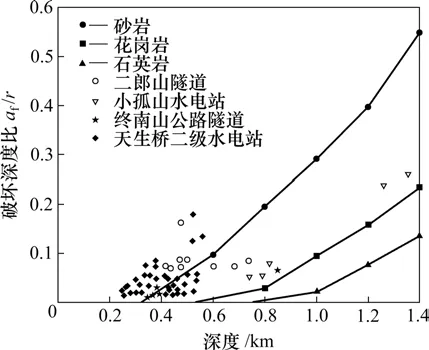
图8 不同种类围岩的脆性破坏深度变化Fig.8 Depth change of brittle failure of different kinds of rock mass with increment of depth

由图 8中二郎山隧道(以砂岩为主)、小孤山水电站引水隧洞及高压流道(石英二长岩)、终南山公路隧道(混合花岗岩、片麻岩)、天生桥二级水电站引水隧洞(白云岩、灰岩)等工程岩爆破坏深度比变化可看出：已发生岩爆破坏深度比与基于中国大陆地应力分布规律、利用式(3)所得到的不同围岩种类脆性破坏深度变化具有较好的一致性，其中，略有变化部分主要是受节理面等构造面的影响，使得破坏深度比预测结果略大。可利用图8对中国地应力分布规律下洞室围岩脆性破坏深度进行前期预测。

4 结论

(1)不同应力组合对岩体破坏深度的影响不同，在应力比较高、与洞群大角度相交时，最不利于洞室的稳定。随着洞室间距增加，洞顶应力集中加剧，脆性破坏深度逐渐等于单洞室下脆性破坏深度。

(2)对不同形状的洞室，围岩应力集中系数不同。在实际工程中，应针对初始应力场特征，选择适宜的洞室形状，可有效降低脆性破坏深度。

(3)脆性岩体属性不同，则起始脆性破坏埋深不同。随着岩石单轴抗压强度增加，脆性破坏深度逐渐降低且破坏深度增加幅度亦逐渐降低，当单轴抗压强度σc(即)大于一定值时，围岩不会发生脆性破坏。

(4)基于中国大陆地应力分布规律，对不同种类岩体洞室围岩脆性破坏进行预测，所得结果与实际工程结果具有较好的一致性，可利用所得结果对地下洞室围岩脆性破坏深度进行预测分析。

[1]谭以安. 岩爆烈度分级问题[J]. 地质论评, 1992, 38(5):439-443.TAN Yi-an. A new classification of rockburst intensity[J].Geological Review, 1992, 38(5): 439-443.

[2]谢兴华, 速宝玉, 詹美礼. 基于应变的岩石类脆性材料损伤研究[J]. 岩石力学与工程学报, 2004, 23(12): 1966-1970.XIE Xing-hua, SU Bao-yu, ZHAN Mei-li. Study on brittle rock failure criterion based on strains[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 1966-1970.

[3]肖洪天, 周维垣. 脆性岩石变形与破坏的细观力学模型研究[J]. 岩石力学与工程学报, 2001, 20(2): 151-155.XIAO Hong-tian, ZHOU Wei-yuan. A mesoscopic model of derormation and failure for brittle rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(2): 151-155.

[4]Martin C D, Kaiser P K, McCreath D R. Hoek-Brown parameters for predicting the depth of brittle failure around tunnels[J]. Canadian Geotechnical Journal, 1999, 36(1):136-151.

[5]Diederichs M S. The 2003 Canadian geotechnical colloquium:Mechanistic interpretation and practical application of damage and spalling prediction criteria for deep tunneling[J]. Canadian Geotechnical Journal, 2007, 44(9): 1082-1116.

[6]吴德兴, 杨健. 苍岭特长公路隧道岩爆预测和工程对策[J].岩石力学与工程学报, 2005, 24(21): 3965-3971.WU De-xing, YANG Jian. Prediction and countermeasure for rockburst in Cangling mountain highway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21):3965-3971.

[7]宫凤强, 李夕兵. 岩爆发生和烈度分级预测的距离判别方法及应用[J]. 岩石力学与工程学报, 2007, 26(5): 1012-1018.GONG Feng-qiang, LI Xi-bing. A distance discriminant analysis method for prediction of possibility and classification of rockburst and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 1012-1018.

[8]安其美, 丁立丰, 王海忠. 福建周宁水电站水压致裂地应力测量及其应用[J]. 岩土力学, 2004, 25(10): 1672-1676.AN Qi-mei, DING Li-feng, WANG Hai-zhong. Research of curst stress measurement and its application with hydraulic fracturing in Zhongning hydro-power station of Fujian Province[J]. Rock and Soil Mechanics, 2003, 25(10): 1672-676.

[9]Rojat F, Labiouse V, Kaiser P K, et al. Brittle rock failure in the steg lateral adit of the lötschberg base tunnel[J]. Rock Mech Rock Eng, 2009, 42(2): 341-359.

[10]Rocscience, 2D plane strain indirect boundary element analysis software, Examine2D 7.0[EB/OL]. [2009]. http://www.rocscience.com.

[11]蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2002.CAI Mei-feng, HE Man-chao, LIU Dong-yan. Rock mechanics and engineering[M]. Beijing: Science Press, 2002.

[12]朱焕春, 陶振宇. 不同岩石中地应力分布[J]. 地震学报, 1994,16(1): 49-63.ZHU Huan-chun, TAO Zhen-yu. Geostress distributions in different rocks[J]. Acta Seismologic Sinica, 1994, 16(1): 49-63.

[13]Fuchs K, Müller B. World stress map of the earth: A key to tectonic processes and technological applications[J].Naturwissenschaften, 2001, 88: 375-371.

[14]景峰, 盛谦, 张勇慧, 等. 中国大陆浅层地壳实测地应力分布规律研究[J]. 岩石力学与工程学报, 2007, 26(10): 2056-2062.JING Feng, SHENG Qian, ZHANG Yong-hui, et al. Research on distribution rule of shallow crustal geostress in China mainland[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2056-2062.

[15]赵德安, 陈志敏, 蔡小林, 等. 中国地应力场分布规律统计分析[J]. 岩石力学与工程学报, 2007, 26(6): 1265-1271.ZHAO De-an, CHEN Zhi-min, CAI Xiao-lin, et al. Analysis of distribution rule of geostress in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1256-1271.