矿山采空区稳定性二级模糊综合评判

吴启红，彭振斌，陈科平，彭文祥，陈乐求

(中南大学 地学与环境工程学院，湖南 长沙，410083)

在矿山采空区稳定性分析、评价和预测中，尽管方法多种多样，但总体上都是基于刚体极限平衡理论或改进的极限平衡理论，而且对边界条件大大进行了简化，在计算中选用的参数被认为是确定的或线性变化的。实际上，不仅采空区中的各种计算参数是不确定和随机的，而且采空区本身是一个不平衡、不稳定的复杂系统，具有不可长期确定性预报和短期统计失效等不足。为此，许多研究者对其进行了研究，如何忠明等[1]利用 FLAC3D软件分别对双层采空区以及考虑应变软化的地下采场开挖顶板稳定性进行了分析；彭欣等[2]利用 ANSYS软件对特大采空区近区开采进行模拟分析；凌标灿等[3-4]运用人工神经网络对采场顶板稳定性进行了动态预测和工程分类；周科平等[5]利用人工神经网络，在数值模拟的基础上建立安全顶板厚度非线性神经网络预测模型；李晓静等[6]采用层次分析法分析了影响地下洞室围岩稳定性的各个因素；董志宏等[7]采用数值流行元方法对地下洞室稳定性进行探讨；赵明华等[8-9]对溶洞顶板稳定性进行了分析。在此，本文作者运用多级模糊评判理论[10]，选取15个影响采空区稳定性的因子，建立二级模糊综合评判模型，以便为矿山采空区稳定性评价提供可行且可靠的思路和方法。

1 评价模型的建立

1.1 影响采空区稳定性的主要因素、因子量化及模型的建立

采空区变形破坏总是在若干特定影响因素[11-12]作用下产生的，而每一影响因素又由若干因子组成。根据一些研究者对采空区稳定性影响因素的研究成果，以及笔者对大量稳定或失稳采空区的数据统计分析结果可知：采空区稳定性主要与矿区地质条件(如岩体结构、构造、围岩蚀变、夹石)、岩石各种性能(如抗压强度、抗拉强度、抗剪强度、抗水性)、区域水文地质(矿区主要充水含水层、矿区断裂及其破碎带、老窿水和生产矿井)、其他特征因素(岩石风化程度、开挖面积、防护措施、顶板厚度与跨度的比值)有关，在此，本文作者据上述4类因素，用15项因子[13-14]作为模糊综合评价预测的因素及因子，由此构造采空区稳定性二级模糊综合分析模型，如图1所示。

建立模糊综合评价模型时，一般需对上述因素的因子进行量化[10-12]。采空区的稳定性划分为3个级别：稳定采空区、局部不稳定采空区和不稳定采空区，分别用Ⅰ，Ⅱ和Ⅲ表示。通过对研究程度较高的变形破坏采空区特征数据进行统计分析，可确定上述15项因子影响采空区破坏的各级界限值。但由于各因子的物理意义不同，量纲也不一致，为了保证各因子具有等效性和同序性，需在进行模糊计算之前，对原始数据进行处理，将各级界限进行标准化。其标准化的处理过程是将每个因子所测的实际数据除以表1中这个因子中假设的最大实际数据(见表1)。

1.2 因子评价隶属函数的建立

预测因子分定性和定量2类，前者属离散变量，后者属连续变量。根据建立隶属度的基本原则，在采空区稳定性评价中，采用专家评定法和公式法2种方式。对于表1中的离散型变量，因其因子的离散化，主要采用专家评定法取值，如表2所示。而对连续变量，则建立了代表隶属度和预测因子之间的函数关系即隶属函数，其隶属度可通过代入因子实测值经计算得到。隶属函数种类很多，综合各因子数据的分布特征，采用三相线性隶属函数，其公式如下：

式中：x为定量因子的实测值标准化后的数值；s1，s2和s3分别为相应定量因子在空区稳定、局部不稳定、不稳定这3种状态下标准化后数值(见表1)。

按上述方法和步骤，在本系统中，因素集U、因子集Un、评价集V分别为：

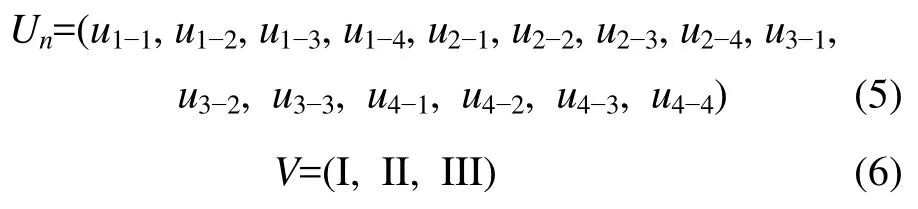
式中各参数含义见图 1。根据各参数的分级标准，作出各参数的隶属函数曲线，见图2。

1.3 模糊综合评价模型的建立

1.3.1 各单因素中因子评价(一级模糊评价)矩阵的确定

将变形破坏采空区或要评价的采空区预测因子的定性因子隶属度按表2确定，定量因子将其实测值(标准化后)代入相关隶属函数中，求得各参数对Ⅰ，Ⅱ和Ⅲ级的隶属度，由此可得到各单因素分别对Ⅰ，Ⅱ和Ⅲ级采空区的评价矩阵Rn， 即

表1 评价因子及分级标准表Table 1 Evaluation genes and grading standards

表2 离散型因子隶属度取值表Table 2 Value of membership grades of discreteness variable gene

图2 各定量参数隶属函数曲线Fig.2 Membership functions of each quantitative parameters

式中：Y为各评价因子的隶属度；n和i均为1，2，3，4。

1.3.2 各因素和因子权重的确定

目前，国内通常采用的确定权数[15]的方法有2种：一种是专家打分法，另一种是采用 Saaty提出的 1～9标度法。这2种方法均带有一定的主观性。为了更合理确定各因素权重A和各因子权重An，采用计算机反演权重A及An，其过程如下。

(1)初步确定和给出各因素因子权数，权重A和An分别是由各评价因素、评价因子权数分配构成的1个 1×4及 1×4，1×4，1×3，1×4 阶矩阵，即A=(a1，a2，a3，a4)，An=(an-1，an-2，an-3，…，an-i)。

式中：an为评价因素的权重；an-i为评价因子的权重；n与i均为1，2，3，4。通过对影响采空区稳定性的内因、外因进行研究，认为矿区地质，、岩石各种性能、区域水文地质等因素对采空区稳定性影响最大，而其他因素次之。据此可得到各评价因素权数，同理可得出各评价因子权数。

(2)权值反演。首先，在研究区内选取一些已知稳定程度的采空区，然后，将这些采空区因子的实测值代入隶属函数中，求出各采空区的单因素模糊关系矩阵Rn和多因素模糊关系矩阵R；在各因素、因子权数不变的情况下，任意给定一组权数，并将权重A和An以及矩阵R和Rn分别按先后顺序合成运算，得出单因素评价(一级评价)Bn；最后，根据最大隶属度原则判断采空区的稳定性等级。若计算得到的采空区的稳定性等级与实际等级不符，则改变权数A，并按上述步骤重新计算，直到得出与实际值完全符合的结果为止。权值的整个反演过程见图3，其中：“◦”表示合成运算为加权平均型运算。

图3 权值反演计算过程框图Fig.3 Block diagram of course of inversing weight value

需指出的是：单个采空区的权值反演具有多解性，而多个采空区的权值反演的公共解则是唯一的，这个唯一的公共解就是所要求的权值。 从因子权值的反演过程可知：通过程序反演的因子权值具有较大的可靠性，可据该权值建立模糊评判模型，用于评判那些未知稳定程度的采空区。通过运用上述方法反演，得到各因素和因子权重，见表3。

表3 评价因素及因子两级权重分配表Table 3 Distribution of two-stage weight of evaluation factors and genes

1.3.3 求解单因素评价矩阵

根据已求得的单因素评价矩阵Rn及单因素中各因子权重An，按一定合成运算，可得单因素评价(一级评价)向量Bn，采用的合成运算为加权平均型运算，即

这样，可以以权重综合反映各因子对采空区稳定所作的贡献。

1.3.4 求解综合评价向量

由上述各单因素评价结果可得二级模糊评价矩阵R，再根据表3中各因素权重A，按加权平均型合成运算，得综合评价(二级评价)向量B，即

最后，根据B中向量按择近原则进行评价。至此，建立了采空区稳定性二级模糊综合评价模型。

2 模糊评价实例分析

根据某矿山采空区的工程地质条件，将相应的采空区稳定性模糊评价因子进行标准化取值，如表 4所示。

表4 采空区参数取值表Table 4 Parameter value of gob area

2.1 一级模糊评价

将标准化值代入上述相应的隶属函数中，确定各单因素分别对Ⅰ，Ⅱ和Ⅲ级采空区的综合评价结果。

(1)矿区地质特征：

由表3得：

(2)岩石各种特征：

由表3得：

(3)区域水文地质特征：

由表3得：

(4)其他特征：

由表3得：

2.2 二级模糊评价

由上可得二级模糊评价矩阵R：

据表3得各因素权重：

由此可见：该采空区属于III级的隶属度最大，为0.410 9。按贴近度原则，可以判定该采空区为不稳定采空区。经现场实际调查及采用其他采空区稳定性分析方法对该采空区进行验证，模糊评判结果与实际采空区实际结果相吻合，与其他采空区稳定性分析方法所得的结果也相符。

3 结论

(1)考虑到对采空区稳定性分析不仅具有一定的随机性，同时具有很强的模糊性，引入系统理论中的模糊综合评判方法、层次分析方法建立多级模糊评判模型。该模型能综合考虑多种因素的影响及其相互关系，简单实用，且评判结果可靠。

(2)采用计算机反演权重的方法对各因素、因子的权重取值，结果较精确。

(3)二级模糊综合评判模型可针对各类复杂的采空区，通过选取不同的因素、因子进行稳定性评价，具有较强的实用性和灵活性。

[1]何忠明, 彭振斌, 曹平, 等. 双层采空区开挖顶板稳定性的FLAC3D数值分析[J]. 中南大学学报: 自然科学版, 2009, 40(4):1066-1071.HE Zhong-ming, PENG Zhen-bin, CAO Ping, et al. Numerical analysis for roof stability of double gob area after excavation by FLAC3D[J]. Journal of Central South University: Science and Technology, 2009, 40(4): 1066-1071.

[2]彭欣, 崔栋梁, 李夕兵, 等. 特大采空区近区开采的稳定性分析[J]. 中国矿业, 2007, 16(4): 70-73.PENG Xin, CUI Dong-liang, LI Xi-bing, et al. Adopt the stability analysis that the empty area near area mines greatly especially[J]. China Mining Magazine, 2007, 16(4): 70-73.

[3]凌标灿, 彭苏萍, 孟召平. 采场顶板稳定性动态预测及控制研究[J]. 工程地质学报, 2003, 11(1): 44-48.LING Biao-can, PENG Su-ping, MENG Zhao-ping. Dynamical evaluation and control of the roof stability for longwall top-coal caving face[J]. Journal of Engineering Geology, 2003, 11(1):44-48.

[4]凌标灿, 彭苏萍, 张慎河, 等. 采场顶板稳定性动态工程分类[J]. 岩石力学与工程学报, 2003, 22(9): 1474-1477.LING Biao-can, PENG Su-ping, ZHANG Shen-he, et al.Dynamic engineering classification of stope roof stability[J].Chinese Journal of Rock Mechanics and Engineering, 2003,22(9): 1474-1477.

[5]周科平, 苏家红, 古德生, 等. 复杂充填体下矿体开采安全顶板厚度非线性预测方法[J]. 中南大学学报: 自然科学版, 2005,36(6): 1094-1099.ZHOU Ke-ping, SU Jia-hong, GU De-sheng, et al. The nonlinear forecasting method of the least security coping thickness when mining under complex filling body[J]. Journal of Central South University: Science and Technology, 2005, 36(6): 1094-1099.

[6]李晓静, 朱维申, 陈卫忠, 等. 层次分析法确定影响地下洞室围岩稳定性各因素的权值[J]. 岩石力学与工程学报, 2004,23(S2): 4731-4734.LI Xiao-jing, ZHU Wei-shen, CHEN Wei-zhong, et al.Determining weight of factors in stability analysis of underground caverns by analytic hierarchy process[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S2):4731-4734.

[7]董志宏, 邬爱清, 丁秀丽. 基于数值流形元方法的地下洞室稳定性分析[J]. 岩石力学与工程学报, 2004, 23(S2):4956-4959.DONG Zhi-hong, WU Ai-qing, DING Xiu-li. Stability study of underground cavern with numerical manifold method[J].Chinese Journal of Rock Mechanics and Engineering, 2004,23(S2): 4956-4959.

[8]赵明华, 程晔, 曹文贵. 桥梁基桩端溶洞顶板稳定性的模糊分析研究[J]. 岩石力学与工程学报, 2005, 24(8): 1376-1383.ZHAO Ming-hua, CHENG Ye, CAO Wen-gui. Fuzzy method for the stability analysis of cave roof under pile tip in karst region[J]. Chinese Journal of Rock Mechanics and Engineering,2005, 24(8): 1376-1383.

[9]黎斌, 范秋雁, 秦风荣. 岩溶地区溶洞顶板稳定性分析[J]. 岩石力学与工程学报, 2002, 21(4): 532-536.LI Bin, FAN Qiu-yan, QIN Feng-rong. Analysis on roof stability of karst cave in karst areas[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 532-536.

[10]杨纶标, 高英仪. 模糊数学原理及应用[M]. 4版. 广州: 华南理工大学出版社, 2006.YANG Lun-biao, GAO Ying-yi. Theory and applications of fuzzy mathematics[M]. 4th ed. Guangzhou: South China University of Technology Press, 2006.

[11]温庆华, 童保国. 哈拉沟煤矿煤巷顶板稳定性影响因素分析[J]. 煤炭技术, 2009, 28(1): 96-98.WEN Qing-hua, TONG Bao-guo. Analysis on influence elements of coal roadway roof stability in Halagou Coal Mine[J].Coal Technology, 2009, 28(1): 96-98.

[12]张林, 杨志刚, 钱庆强, 等. 溶洞顶板稳定性影响因素正交有限元法分析[J]. 中国岩溶, 2005, 24(2): 156-159.ZHANG Lin, YANG Zhi-gang, QIAN Qing-qiang, et al.Analysis to factors affecting the stability of karst cave ceiling with orthogonal definite element method[J]. Carsoligica Sinica,2005, 24(2): 156-159.

[13]张晓君. 影响采空区稳定性的因素敏感性分析[J]. 矿业研究与开发, 2006, 26(1): 14-16.ZHANG Xiao-jun. Sensitivity analysis of factors influencing the stability of mined-out area[J]. Mining Research and Development, 2006, 26(1): 14-16.

[14]《工程地质手册》编写委员会. 工程地质手册[M]. 4版. 北京:中国建筑工业出版社, 2007.The Compilation Committee of Engineering Geology Handbook.Engineering geology handbook[M]. 4th ed. Beijing: China Architecture and Building Press, 2007.

[15]曹文贵, 张永杰. 地下结构岩体质量分类的变权重二级模糊综合评判方法研究[J]. 岩石力学与工程学报, 2006, 25(8):1612-1618.CAO Wen-gui, ZHANG Yong-jie. Study on two-stage fuzzy synthetic judgment method based on interval AHP analysis method to the classification of rock quality in underground structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(8): 1612-1618.