横向预应力加固板梁桥的有限元分析
金 花, 孙立功
(陕西铁路工程职业技术学院,陕西渭南 714000)
0 引言
据桥梁病害状况调查显示:大量既有高速公路中常用的板梁桥出现了不同程度的结构病害。该类桥梁的损伤与破坏主要表现为桥面板的板间铰缝混凝土完全开裂或脱落,造成板之间的横向联系破坏,导致单板承受车轮荷载作用,一般称这种现象为“单板受力”,单板受力严重破坏了桥梁的整体性,降低了桥梁的承载能力,给行车安全带来了隐患。如何采用经济、有效的加固技术预防出现“单板受力”和解决出现的“单板受力”现象已经成为了有关部门亟需解决的问题。
1 桥梁概况
该桥横向由 8块空心板组成,板间的横向连接通过铰缝来实现,桥面宽度为 13.25 m。板的混凝土标号为 C50。本桥采用了横向预应力加固法,加固设计中采用的钢绞线为 ASTMA416—90a标准 270级高强度低松弛钢绞线,公称直径为 15.24mm。全桥横断面如图1所示。

图1 全桥的横截面图(单位:cm)
通过对钢绞线数量、布置位置的比较得出横向预应力加固法中较为合理、经济的钢绞线的布置方式是:从跨中向两侧垂直于桥的纵向轴线对称布置,顺桥向跨中一束,两端支座附近各一束,共计 3束;沿梁高方向横向预应力筋布置在空心板底偏上 0.4m处(板的中性轴以下且方便打孔的位置),即在梁体空心处打孔穿筋,预应力筋的两端与两侧边板的相应位置刚性连接形成一体。为保证锚下局部应力不至于过大,在空心板边板侧面应设置具有一定厚度且大小适当的钢板以减少锚下局部应力[1]。
加固设计中钢绞线张拉力,按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)的规定,为保证锚具不松弛,预应力张拉时实际有效的横向张拉应力在大于钢绞线标准强度的 40%范围内某一经济的吨位即可,故设计张拉控制力为 129.3 kN,已考虑了钢筋回缩、锚具变形及垫板压密、预应力钢绞线应力松弛和孔道摩擦等造成的预应力损失[2]。
2 有限元模型的建立
利用 ANSYS软件对铰接板梁桥建立了空间实体有限元模型[3-4]。
空心板、铰缝均采用空间 8节点 6面体单元 Solid45建模,对于板梁桥的钢筋不予考虑,每个节点有 3个平动自由度。由于现浇铰缝混凝土的收缩,铰缝与预制板新老混凝土的粘结性差,铰缝与板基本是分离的,对旧桥尤其如此,而且此缝只是为板的安放而预留的缝,依设计初衷是可以不填充的,,故可以认为板与铰缝只在上缘处连结,而下缘是分离开的。在建立模型时,可将各板与铰缝分开建模,然后耦合板与铰缝上缘的自由度即可。
桥面铺装层分上下两层:沥青混凝土为上层、水泥混凝土为下层。上层沥青混凝土层仅作为传力层和保护层,不参与受力,故不需要建立该层的模型而只将其作为恒载来考虑;下层水泥混凝土层与原受力结构即与板共同受力,用实体单元 Solid45来建模。
预应力钢绞线采用三维杆单元 Link8单独建模,杆单元与实体单元之间的联结通过将同一位置的节点对的自由度耦合来实现,预加力采用等效温度荷载来施加。
至于有限元模型的边界条件,固定支座以三向约束 (X,Y,Z)进行施加;移动支座以Z轴自由,X轴和Y轴固定进行施加。施加的约束位于理论支承线处有限元模型截面的下边缘节点上。在计算模型中,分别在各板的跨中位置中心处施加单位竖向荷载,再根据各板的挠度比例关系求得各板挠度横向分布影响线,以挠度横向分布影响线的平缓程度来探讨荷载的横向分布[5]。因结构的对称性,仅分析其中 4块板的挠度横向分布影响线。
3 有限元法与铰接板法计算横向分布影响线的对比分析
对铰接板桥,在施加横向预应力前,各板间横向联系较弱,可视为铰接,故可根据传统铰接板理论来计算横向分布影响线,并与 ANSYS计算的挠度横向分布影响线进行比较。结果分别如图2所示,可知按两种方法所得的影响线差别很小,二者计算结果基本吻合。说明本文计算模型的正确、有限元方法有效,故可采用此方法来计算铰接板桥的横向分布影响线。

图2 1~4号板铰接法和有限元法的挠度横向分布影响线
4 对荷载横向分布规律的探讨
建立跨径为 25m的简支铰接板梁桥的有限元模型,得出图3所示挠度横向分布影响线。从边板到中板挠度横向分布影响线依次平缓,即幅值差逐渐减小,说明荷载作用在边板时不均匀性最严重,当荷载位置逐渐靠近中间时其荷载横向分布趋于均匀。
4.1 宽跨比对荷载横向分布的影响
建立跨径分别为 20 m、25 m、30m的简支铰接板梁桥的有限元模型,3个模型的宽跨比μ=b/l依次为:0.66,0.53,0.44,分别求得各板对应于不同宽跨比时的挠度横向分布影响线如图4所示:随着宽跨比的减小即相同条件下跨径的增大,其挠度横向分布影响线逐渐变的平缓即幅值差逐渐减小,说明其荷载横向分布趋于均匀;相反,相同条件下跨径越小,其荷载横向分布越不均匀。

图3 1~4号板的挠度横向分布影响线

图4 1~4号板不同宽跨比时的挠度横向分布影响线
从力学角度分析,相同条件下跨径越大越接近于细长梁,因此,越有利于荷载的横向分布。
4.2 斜交角对荷载横向分布的影响
建立跨径 25m,斜交角为 0°、15°、30°、45°的简支铰接板梁桥有限元模型,求得各板对应于不同斜交角时的挠度横向分布影响线如图5。斜交板梁桥的荷载横向分布规律和相应的正交板梁桥荷载横向分布规律类似,且随着斜交角增大其荷载横向分布逐渐不均匀;当斜交角为 15°时其挠度横向分布影响线与正交板梁桥很接近,故对于斜交角不超过 15°的斜交板梁桥可按正交板梁桥来计算,这与规范是相符的。
5 板梁桥加固效果的评析
以各板挠度横向分布影响线竖标值的最大值 ηmax、最小值 ηmin的差值 Δη=ηmax-ηmin在加固前、后的变化 λ(Δη)=(Δη加固前-Δη加固后)/Δη加固前作为评价加固效果的指标 。

图5 1~4号板不同斜交角时的挠度横向分布影响线
5.1 宽跨比对加固效果的影响
建立跨径分别为 20、25、30 m的简支铰接板梁桥的有限元模型,3个模型的宽跨比 μ=b/l依次为:0.66,0.53,0.44,求得对应于不同宽跨比时的加固效率指标如表1所示:随着宽跨比的减小其加固效率逐渐增大,且对于同一宽跨比的板梁桥来说从边板到中板加固效果逐渐增强。
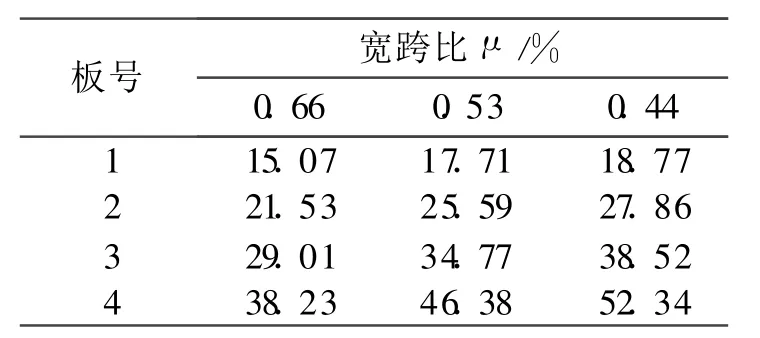
表1 1~4号板应于不同宽跨比时的 λ值
5.2 斜交角对加固效果的影响
建立跨径为 25 m,斜交角分别为 0°、15°、30°、45°的简支铰接板梁桥的有限元模型,求得对应于不同斜交角时的加固效率指标如表2所示:横向预应力加固法对斜交板梁桥同样能取得较好的加固效果,但其加固效果不如正交板梁桥明显;随着斜交角的增大其加固效率逐渐减弱,且对于同一宽跨比的板梁桥来说从边板到中板加固效果逐渐增强。

表2 1~4号板应于不同斜交角时的 λ值
6 结论
横向预应力加固法能有效的改善铰接板梁桥的荷载横向分布,增加板间的横向联结,避免单板受力现象,且随着宽跨比的减小其加固效率增大。但斜交板梁桥的加固效果不如正交板梁桥明显,对于同一宽跨比的板梁桥来说无论正交还是斜交,从边板到中板加固效果逐渐增强。

