枞树形榫连结构接触应力的有限元分析及建模研究

魏大盛，王延荣

(北京航空航天大学 能源与动力工程学院，北京100083)

1 引言

对许多物理和工程问题的描述都涉及接触现象，以航空发动机为例，包括装配时的过盈配合、传动系统中的齿轮传动、叶盘榫连结构等，接触的物体在接触界面上的相互作用较为复杂，是发生损伤和破坏的主要原因。

航空发动机榫连结构，是典型的接触结构，在热、机械载荷的作用下，接触部位通常存在高应力梯度，随着结构使用寿命的日益增长，接触疲劳、微动疲劳问题在工程中逐渐得到重视[1～3]。文献[4]对燕尾形榫连结构的接触应力进行了深入分析，准确计算了高应力梯度位置的接触应力分布，并探讨了网格密度对计算结果的影响，改善了国内以往针对榫连结构分析时计算结果精度较低的情况[5，6]。

相比于压气机的燕尾形榫连结构，涡轮的枞树形榫连结构除承受离心载荷之外，还承受较高的热载荷作用，同时结构复杂，接触对数目增加，这都增加了接触分析的难度。正因如此，本文首先对典型赫兹接触问题进行计算分析，并同解析解进行对照，以明确采用有限元法处理接触问题的流程及注意事项；其次，针对某发动机三齿枞树形榫连结构的接触问题展开分析，重点考查建模方式对接触应力求解精度的影响。

2 赫兹接触问题

接触问题的高度非线性使其求解难度大大提高，目前有限元法是处理接触问题的首选方法，但其主要有以下几个难点：解不易收敛；解收敛，但合理性及精度不好评价；求解时计算量过大，尤其是三维问题。因此，在开展榫连结构接触应力分析之前，首先采用有限元法对具有解析解的赫兹接触问题进行分析[7]，以此明确有限元法求解接触问题的一般流程。

以两平行轴弹性圆柱体的接触问题作为算例，其几何形式及接触体内部的应力分布见图1。采用有限元程序MSC.MARC建立的相应的分析模型见图2，有限元解及解析解同时在图3、图4中给出(图中，formula表示解析解，fem表示有限元解)，表1则给出了几个关键数值。由接触面(Y=0)以及对称面(X=0)的应力计算结果来看，接触区内部应力的解析解同有限元解吻合很好，接触表面应力的解析解同有限元解则略有差异，由数值计算误差所致。

以上计算分析表明，只要模型建立合适，求解方法得当，有限元法在处理接触问题时可以给出足够高的精度。

图1 赫兹接触形式及应力分布Fig.1 Hertz contact and stress distribution

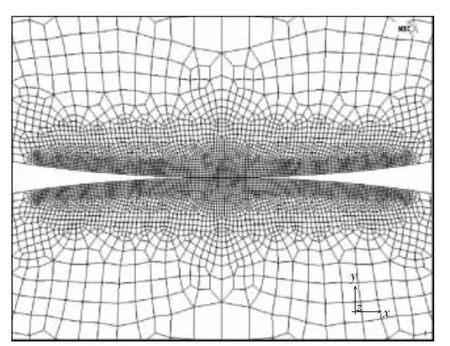
图2 赫兹接触的有限元模型Fig.2 Finite element model of hertz contact

图3 接触面(Y=0)上的应力分布Fig.3 Stress distribution on the contact surface

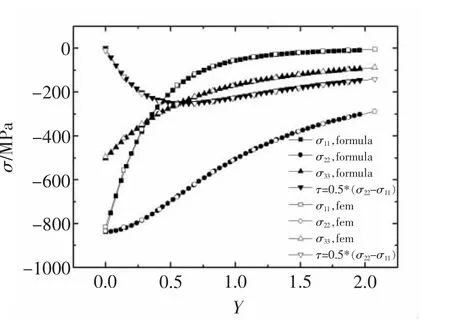
图4 接触体内部沿对称面(X=0)的应力分布Fig.4 Inner stress on the symmetrical plane

3 枞树形榫连结构的有限元分析

3.1 接触应力分析

在赫兹接触问题计算分析的基础上，开展了某发动机真实叶盘榫连结构的接触应力分析。其结构如图5所示，共有三对接触齿对，接触面角度约为40°，三对齿的接触区长度均接近1.8 mm，接触区边缘圆角半径约0.675 mm。

表1 赫兹接触的有限元解及解析解的对比Table 1 Numerical solution by FEM and analytic one

图5 枞树形榫连结构几何模型Fig.5 Geometrical model of fir tree attachment

以往相关分析中接触区网格稀疏，无法反映细节特征，因此本文的有限元模型采用了较密的网格密度。三对齿的接触区网格均初步划分为400个，边界层采用规则网格划分，内部采用自由网格划分。有限元模型见图6，单元43 521个，节点44 995个。

图6 枞树形榫连结构有限元模型Fig.6 FE model of fir tree attachment

计算时边界条件主要考虑了离心力、温度场以及未参与有限元建模的叶片部分的拉力，其作用于叶片上端面。枞树形榫槽的接触对数量较多，增加了接触分析时收敛的难度。因此计算中采用了固定步长时间增量，增量步为100；同时载荷也采用了逐步增加的方式，其中转速随时间成正比增加，而拉力则与时间成非线性变化，具体对应关系可由离心力公式推导得出。计算结果表明，第三对接触齿接触区的下边缘点接触应力最大，见图7和图8。当然，计算时采用的几何模型较为精确，这同实际加工时具有尺寸公差的情况不同，不同齿距偏差组合对不同榫槽/榫头齿对接触次序、接触应力大小都有较大影响，因而接触应力最大点的位置在实际情况中可能有所变化。

3.2 接触应力计算结果的收敛性分析

由于接触区边缘存在高应力梯度，同时网格密度对接触区边缘的应力值也有较大影响[8]，因此，为精确计算接触区边缘应力，将接触区网格分别细化2倍及3倍，以此考查有限元结果的收敛性。设接触区四边形单元边长为LE，接触区边缘圆角半径为RF，则参数LE/RF可用于度量接触区网格密度。不同网格密度有限元模型的参数见表2。

不同网格密度有限元模型的接触应力计算结果见表3，表4则给出了相邻网格密度计算结果的相对误差。据此，可根据下式对收敛性做出判断[8]：

图7 三对齿接触压力σ22比较Fig.7 Contact stress component σ22on each tooth

图8 接触压力σ22分布Fig.8 Distribution of contact stress component σ22

式中n表示第n个计算模型。根据此收敛判据不断对接触区网格进行细化，当两次计算结果相差不超过5%时可认为计算收敛。由表3中的计算结果可知，随着网格密度的增加，峰值应力计算结果提高，计算逐渐收敛。网格2同网格1的计算结果相差最大9%，说明接触区网格密度为400时的模型计算结果并未收敛，而网格3同网格2的计算结果相差在3%以下，网格2的计算结果已经达到收敛。图9中给出了枞树形榫槽第三齿接触区应力计算结果的分布及收敛趋势。

图10中给出了网格对收敛的影响趋势：对于单齿燕尾形榫连结构，沿接触区划分450个网格可保证计算收敛；对于三齿枞树形榫连结构，沿接触区划分1 000个网格可保证计算收敛。当然，对于不同的计算模型，网格划分的密度应同几何参数(特别是接触区长度及接触区边缘圆角半径)、受力状态密切相关。

3.3 接触区计算网格的改进

接触是典型的非线性问题，求解不易收敛，计算时间较长。而前面的分析表明，传统榫连结构接触区边缘存在较高的应力梯度，其应力计算结果依赖于网格密度，较为稠密的网格划分可以满足计算精度，但同时计算时间会显著增加。因此，有必要对前面采用的计算网格进行改进，以提高计算效率。对于本次研究中的榫连结构，其高应力梯度区域，也即需要较密网格划分的部分，仅存在于叶/盘接触区的边缘部分，因此仅对该部分的网格进行细化即可。改进后的计算网格如图11所示。

表2 不同网格密度的有限元模型Table 2 FE models of different grids

表3 不同网格密度模型第三齿应力结果MPaTable 3 Contact stress from different grids on the third tooth

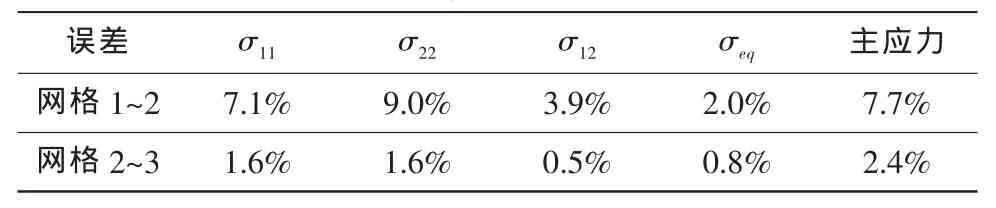
表4 不同模型计算误差分析Table 4 Error analysis of different FE model

图9 不同模型第三齿接触区应力σ22分布Fig.9 Distribution of σ22on the third tooth

图10 计算收敛性分析Fig.10 Convergence analysis

图11 改进后的计算网格Fig.11 Improved grids

采用改进后的网格进行分析，接触应力计算结果差别不大，但计算时间显著减少，这对于后续的三维榫连结构的计算分析至关重要。

4 结论

本文采用有限元法对经典赫兹接触问题以及三齿枞树形榫连结构的接触应力展开了分析，并重点研究了网格疏密程度对数值解的影响及由此带来的收敛性问题，得出了一些具有工程意义的结论：

(1)榫连结构接触区边缘存在显著的应力梯度，这是产生微动疲劳磨损的重要因素。

(2)以往对于榫连结构接触应力的分析，其精度明显不够，这无疑将使微动疲劳寿命的计算精度降低；增加高应力梯度位置的网格密度，有助于计算精度的提高。

(3)枞树形榫槽的危险位置出现在第三齿接触区下边缘点位置，但此结论将受到齿距公差等现实条件的影响。

本文以接触应力分析作为重点，研究表明有限元建模方式对接触应力结果有较大影响，密集的网格划分可以准确刻画接触区应力的细节特征，但同时也使得计算时间急剧增加，如何同时保证计算精度及效率，相应的建模方式还需深入探讨。另外，榫连结构几何参数对接触应力的影响，微动疲劳寿命的评估，也将作为下一步的研究工作。

[1]何明鉴.机械构件的微动疲劳[M].北京：国防工业出版社，1994.

[2]古远兴.高低周复合载荷下燕尾榫结构微动疲劳寿命研究[D].南京：南京航空航天大学，2007.

[3]刘道新，刘 军，刘元镛.微动疲劳裂纹萌生位置及形成方式研究[J].工程力学，2007，24(3)：42—47.

[4]魏大盛，王延荣.榫连结构接触面几何构形对接触区应力分布的影响[J].航空动力学报，2010，25(2)：407—411.

[5]温卫东，高德平.榫头/榫槽接触问题边界元分析[J].航空动力学报，1992，7(2)：117—120.

[6]郑旭东，蔚夺魁，王兆丰，等.某型航空发动机涡轮叶片和轮盘榫齿裂纹故障力学分析[J].航空发动机，2005，31(3)：35—38.

[7]Johson K L.接触力学[M].徐秉业，罗学富，译.北京：高等教育出版社，1991.

[8]Sinclair G B，Cormier N G，Griffin J H，et al.Contact Stresses in Dovetail Attachments:Finite Element Modeling[J].Journal of Engineering for Gas Turbines and Power，2002，124：182—189.