推力磁轴承的优化设计与有限元分析

杨芳芳，吕建超

(中国燃气涡轮研究院，四川 成都 610500)

1 引言

电磁轴承作为一种新颖的非接触式支承部件，因具有无接触、无润滑、无磨损、少维修、寿命长、可靠性高等特点和良好的转子动力学特性而得到学术界和企业界广泛的关注。目前，航空航天工业已成为国际上电磁轴承应用的主要领域之一，电磁轴承可大大提高航空技术的现代化水平。主动推力磁轴承是电磁轴承系统中的一种，由于其具有转子位置、轴承刚度和阻尼可由控制系统确定等优点，在磁悬浮应用领域中得到了广泛的应用[1]。

在工程实际中，经常遇到在已知定子内、外径的条件下设计主动推力磁轴承。本文在已知定子内、外径的条件下，根据承载力和温升的要求设计了一套推力磁轴承，并利用有限元分析软件对推力磁轴承的电磁特性进行了验证。

2 推力磁轴承优化设计

推力磁轴承的结构示意图如图1所示。

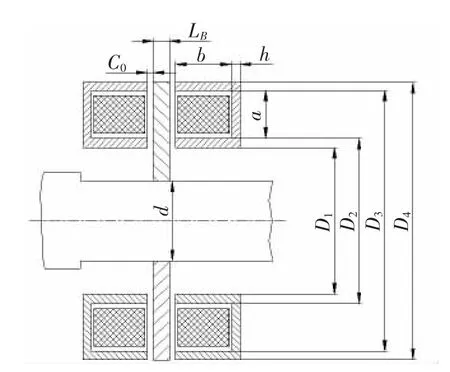
图1 推力磁轴承示意图Fig.1 Scheme of thrust electromagnetic bearings

推力磁轴承最大名义悬浮力Fmax为[2，3]：

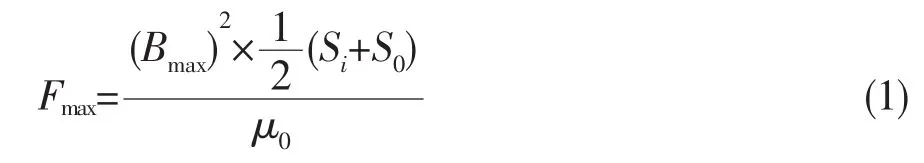
现取相等的内、外环面积，则：

由此可知：

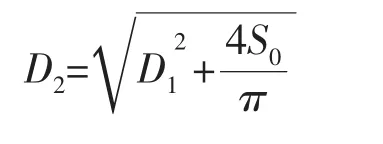
如果磁轭高度h太小，可考虑取最小磁轭工艺尺寸，一般h≥3 mm。并令推力盘宽度LB=1.5h。

线槽深度b未知，考虑磁路方程定子部分的影响，令

可得：

实际设计时要考虑实际线径(标称线径)的规格，并重新计算j的值。下面分别在给定的承载力(最大)、允许的温升及工作气隙的磁感应强度约束条件下，以体积最小为目标函数进行优化。

(1)承载力：Fmax≥W。由于计算内、外磁环面积时已考虑，故在目标函数中不另行考虑。

(2)实际温升：

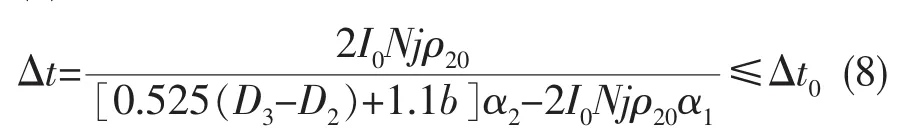
整个定子中铁芯的体积：

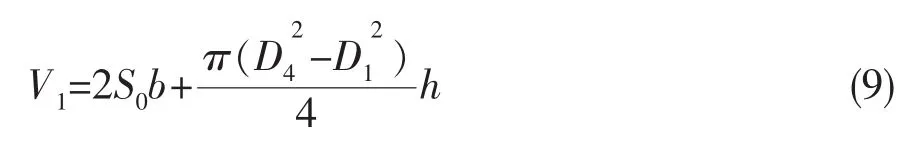
定子中含铜的体积：

设最小体积为目标函数f(X)，考虑参数约束条件，数学模型可表示为：

针对上述优化数学模型可采用复合形法、罚函数法、序贯加权因子(SWIFT)法等优化算法优化得到最优推力磁轴承结构。

3 优化算列

在一工程实例中，已知定子外径D4为119 mm，定子内径D1为65.5 mm，轴向承载力W为1 800 N，安全系数ns为1.1，定子的材料为1J22，其最大磁感应强度Bmax为2.2 T，工作气隙c0为0.5 mm，偏置电流 I0为2.5 A，最大电流密度 jmax为4.5 A/mm2，填充系数 Kc为 0.9，允许温升 Δt0为 150℃，铜线 20℃时的电阻率 ρ20为 0.018 Ω·mm2/m，电阻温度系数 α1为0.004 261℃-1，给定散热条件下的散热系数α2为20 W/(m2·℃)。

优化得到的结构参数见表1，优化设计的推力磁轴承的结构见图2。

表1 优化参数Table 1 Optimized parameters

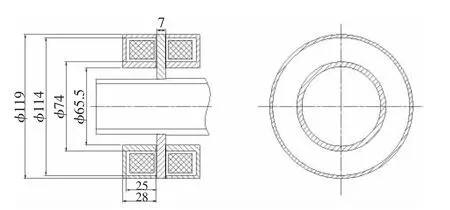
图2 推力磁悬浮轴承结构Fig.2 The structure of thrust magnetic bearings

4 推力磁轴承有限元分析

电磁轴承电磁力的计算方法有磁路方法和场域方法两种。场域方法作为一种更精确的分析方法，以数值计算为基础，可以更加细致地考察诸如磁场分布、边缘效应、极间耦合、涡流、轴承结构等因素的影响。常见的数值法有有限元法和边界元法。

电磁场内在规律由电磁场Maxwell基本方程组来表述，电磁轴承中的磁场分布同样服从Maxwell方程组[4]。Maxwell方程组是分析和计算电磁场问题的出发点。有限元法计算的未知量(也称自由度)主要是磁位或电位，其它诸如磁场磁通密度、电流密度、能量、力、损耗、电感和电容可以由这些自由度导出。

推力磁轴承分析属于静态场分析，此时Maxwell方程变为[5]：

同时，当转子处于平衡位置时，推力磁轴承的磁场属于典型的轴对称形式[6]，所以可以采用二维静态磁场分析。

转子处于平衡位置时，对推力磁悬浮轴承作电磁特性分析，此时磁极上施加的工作电流为偏置电流I0。材料不同的各个面积赋予不同的材料特性，其中定子和推力盘的材料为1J22，空气和导线区域材料的相对磁导率μΓ为1。在导线区域施加电流密度载荷，整个结构的最外层节点施加磁力线平行边界条件。

推力磁轴承一侧的有限元模型如图3所示，其磁力线分布见图4。由图中可以看出，空气媒质中的磁力线与分界面近于垂直，而且漏磁现象不严重。

图3 推力磁轴承有限元模型Fig.3 The finite element model of thrust magnetic bearing

图4 磁力线分布图Fig.4 Flux distribution

从图5所示的磁感应强度分布图可以看出，最大磁感应强度在外磁环气隙处。图6所示为气隙中磁感应强度分布图。图中横坐标DIST代表铁芯与推力盘之间的气隙位置。由图6可以看出，内磁环气隙中的磁感应强度达到0.93 T，外磁环气隙中的磁感应强度达到1 T，气隙中的磁感应强度略小于0.5Bmax，此时电磁力为776 N。

图5 磁感应强度分布图Fig.5 The distribution of flux density

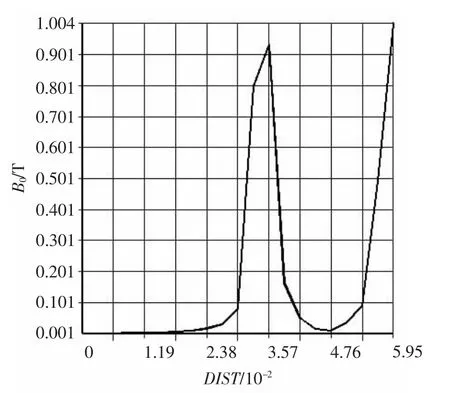
图6 气隙中的磁感应强度分布图Fig.6 Flux density in the air

5 结论

针对工程需要，以承载力最大和温升满足要求为目标优化设计出一套推力磁轴承，并用ANSYS软件对其电磁力进行验算。结果表明，在转子处于平衡位置时，利用有限元计算的推力磁轴承铁芯与推力盘之间的磁感应强度与理论值0.5Bmax仅差0.1 T，此计算结果与文献[6]的结论相符。由此可以推断出，优化设计出的推力磁轴承满足承载力最大的要求。

[1]施韦策G，布鲁勒H，特拉克斯勒A.主动磁轴承基础、性能及应用[M].虞 烈，袁祟军，译.北京：新时代出版社，1997.

[2]Imlach J，M S，Allaire P E.Magnetic Bearing Design Optimization[J].Imech，1998，C277/88，53—60.

[3]Hsiao F Z，Chung C F.Optimum Magnetic Bearing Design Considering Performance Limitations[J].JSME International Journal，1996，39(3)：586—596.

[4]胡业发，周祖德，江征风.磁力轴承的基础理论与应用[M].北京：机械工业出版社，2006.

[5]阎照文.ANSYS工程电磁分析技术及实例详解[M].北京：中国水利水电出版社，2006.

[6]刘淑琴，徐 华.推力电磁轴承的电磁场分析[J].磨擦学学报，2000，20(1)，42—45.