贵州电网短期负荷时间序列的混沌性仿真检验

刘 彬，王红蕾

(贵州大学 电气工程学院，贵州 贵阳 550003)

近年来，混沌理论这门新兴学科在科学研究中的地位日渐凸显。混沌作为一个新的研究方向，已渗透到自然科学和社会科学的各个领域。对于混沌，目前尚无通用的严格定义，一般把不是由随机性外因引起的，而是由确定性方程 (内因)直接得到的具有随机性的运动状态称为混沌。也就是说：混沌是确定性系统表现出来的貌似随机的运动，是对初始条件十分敏感的长期有界的动态行为。混沌不是无序，而是包含着严格的内在规律。混沌研究表明：即使是最简单的非线性系统仍然可以表现出非常复杂的动力学行为。在电力系统领域，已有大量混沌性质方面的研究。例如：电力经济中的混沌，机电系统混沌振荡，分叉、混沌与电压骤降，水轮发电机组调速系统中控制器参数诱发的混沌，静态负荷模型辨识，电站经济运行最优负荷分配，模糊电力系统稳定器的参数优化，短期负荷预测，以及电气设备状态监测中信号的检测方面等。通过研究混沌，人们对事物有了更加深入的了解。目前，电力系统对混沌现象分析主要采用的方法有：庞加莱映射、Lyapunov(李雅普诺夫)指数计算、Melnikov(梅尔尼科夫)方法和频谱分析等。本文运用李雅普诺夫指数法对贵州电网短期负荷时间序列展开研究[1]。

1 李雅普诺夫指数

混沌运动的基本特点是运动对初值条件极为敏感。两个很靠近的初值所产生的轨道，随时间推移按指数方式分离，Lyapunov指数就是定量描述这一现象的量。

1.1 概念及性质

本文研究的贵州电网短期负荷时间序列属于一维动力系统。

对于一维映射：

由于一维映射下只有一个拉伸或折叠的方向，因此可以考虑初值 x0和它的近邻值 x0+δx0。由映射式(1)作一次迭代后，这两点之间的距离为：

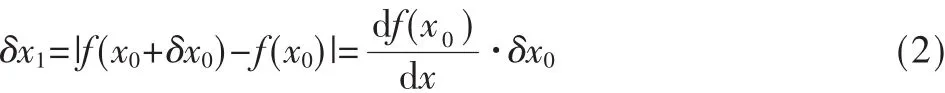
n次迭代后，这两点之间的距离则变为：

式(3)说明这两点要以指数分离，这就是敏感的初始条件，如图 1所示。式(3)中 λ称为 Lyapunov指数，它表示系统在多次迭代中平均每次迭代所引起的指数分离中的指数。

图1 李雅普诺夫指数的定义

由式(3)可得

所以λ代表相邻点之间距离的平均辐射率。利用复合函数的微分规则，有

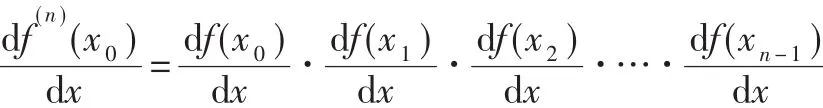
其中：x1=f(x0)，x2=f(x1)=f(2)(x0)…

则 式(4)变为式(5)或式(6)：

一维映射只有一个李雅普诺夫指数，它可能大于、等于或小于零。由上面的讨论得知，若λ＜0，则意味着相邻点最终要靠拢合并成一点，这对应于稳定的不动点和周期运动；若 λ=0，则各点对应周期倍分岔点；若 λ＞0，则意味着相邻点最终要分离，根据敏感的初始条件，其对应于混沌运动。可见，λ由负变为正表明了运动向混沌的转变，故λ＞0可作为系统混沌行为的一个判据[2]。

1.2 小数据量方法

计算李雅普诺夫指数的方法有：定义法、wolf方法、Jacobian方法、p-范数方法、小数据量方法等。综合各种方法的难易度以及计算李雅普诺夫指数的准确度，决定采用小数据量方法计算最大李雅普诺夫指数[3]。该方法的优点在于：(1)对小数据组可靠；(2)计算量并不大；(3)相对容易操作；(4)计算精度较其他方法有明显的改善。小数据量方法的整个计算过程如图2所示。

图2 小数据量方法流程图

2 最大李雅普诺夫指数计算

目前，人们计算最大Lyapunov指数常用wolf的轨线算法，但是轨线法具有明显的缺陷。首先，用此法计算所得结果经常不准确。原因在于按轨线算法寻找不到满足条件的新的邻域轨道时，研究者必须使用较差的轨道，不难想到，较差的轨道使得后来计算出现误差。其次，轨线算法受嵌入参数的影响明显，这是因为嵌入参数影响了重构相空间的形状。但此方法不可避免地要对嵌入参数作出猜测。除此，有人也用矩阵算法来计算最大Lyapunov指数，而矩阵算法的一个明显缺陷是计算过程过于繁难，不易实施。因此，本文采用另一种新方法——小数据量法来计算最大Lyapunov指数值。在混沌研究和实际应用中，有时并不需要计算出时间序列的所有Lyapunov指数谱，而只要计算出最大Lyapunov指数就足够了。故判断一个时间序列是否为混沌系统，只要看最大Lyapunov指数是否大于零就能得出结论。

2.1 用快速傅里叶变换(FFT)估计时间延迟τ和平均周期P

本文收集贵州电网短期负荷时间序列为：贵州电网2009年7月1日到8月31日的负荷值。每隔一个小时取一个负荷值，共1 488个值。

对贵州电网负荷时间序列进行描点，画出贵州电网短期负荷时间序列图，如图3所示。从图中可以看出，贵州电网短期负荷时间序列波形变化具有一定的相似性。

不直接考虑气候等随机因素，利用贵州电网短期负荷时间序列进行FFT变换，根据自相关函数法：对负荷时间序列，先写出其自相关函数，然后作出自相关函数关于时间τ的函数图像，如图4所示。由数值试验结果，当自相关函数(纵坐标)下降到初始值的 1－1/e(大约为0.63)时，所得的时间 τ(横坐标)就是重构相空间的时间延迟 τ(τ取正整数)。

由图4中看出，当自相关函数下降至大约0.63时，所对应的时间大约为3.6，所以得出短期负荷时间序列的时延为4 h。平均周期通过能量光谱的平均频率的倒数估计出来，由MATLAB编程计算得出P为24。

2.2 计算嵌入维数m

由Grassberger和Procaccia提出的G-P算法计算关联维数d。通过关联维数d与嵌入维数m的关系：m≥2d+1确定m的值[4]。

图4 自相关函数法求时延

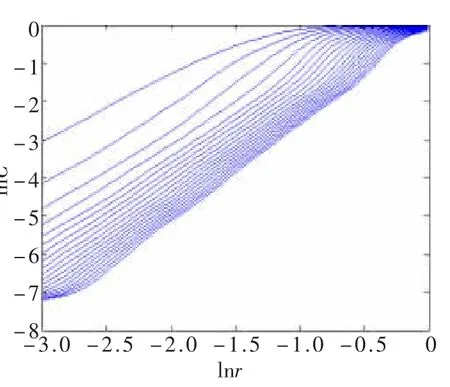
图5 不同m时的lnC-lnr曲线

图6 d随m的变化曲线

此算法依据的方法是：写出时间序列的关联函数C(r)，r为一个给定的值。对于 r的某个适当范围，满足d(m)=ln C(r)/ln r。通过增加嵌入维数m，重复计算C与d，直到相应的维数估计值d不再随m的增长而增长，在一定误差范围内不变为止。从而由拟合求出对应于m的关联维数估计值d。由MATLAB编程调试绘出不同m下d的ln C-ln r曲线(为方便编程，ln C等同于ln C(r))，如图5所示，其直线部分的斜率就是关联维数d。得出 d=1.808 9，2.185 7，2.404 7，2.303 9，2.301 4，2.331 9，2.341 0，2.348 5，2.355 5，2.356 6，2.359 9，2.374 3，2.386 1，2.398 8，2.406 3，2.416 2，2.418 9，2.434 0，2.443 7。

对应d随m变化的曲线图如图6所示。m从2开始，根据图 6得出：当 m为 10、11、12时，关联维数 d趋于平稳，故m取 11。

2.3 重构相空间

相空间重构是从时间序列出发创建一个多维状态空间，它保持了原系统的许多几何不变量不变，这些几何不变量包括不动点的特征值、吸引子的分维数和轨线的 Lyapunov指数等[5]。

根据时间延迟τ和平均周期P重构相空间Yj，并且找最近点，限制短暂分离。对相空间中每个点Yj，计算出该邻点对经过i个离散时间步长后的距离dj(i)；之后对每个i，求出所有j的ln dj(i)平均值y(i)，测量平均分离，即：

其中，q是非零 dj(i)的数目，△t为采样周期。

最后用最小二乘法作出拟合直线，该直线的斜率就是最大 Lyapunov指数 λ1，如图7所示。

根据MATLAB编程调试，作拟合直线计算得出λ1为0.003 1。

由最大 Lyapunov指数 λ1＞0，得出贵州电网短期负荷时间序列具有混沌性。这也为今后利用混沌理论更加深入地对贵州电力系统作出进一步的研究打下了基础。针对电网短期负荷的研究，现在应用最多的就是短期负荷预测。短期负荷预测是电力系统的一项基本工作，是安排开停机机组计划的基础，其预测精度直接影响电力系统的经济效益[6]。混沌理论在短期电力负荷预测中的应用也逐渐增多。混沌理论对负荷序列能进行相空间重构、分形维数计算、最大李雅谱诺夫理论指数计算以及不确定性检验，对影响负荷变化因素的复杂性和随机性有更强的适应性，这可以弥补其他方法在收敛性和鲁棒性等方面的局限性。

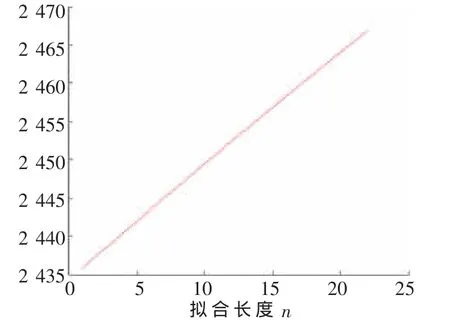
图7 最大Lyapunov指数λ1

[1]黄润生，黄浩.混沌及其应用(第二版)[M].武汉:武汉大学出版社，2005:118-178.

[2]吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社，2002:72-109.

[3]ROSENSTEIN M T， COLLINS J J， DE LUCA C J.A practical method for calculating largest Lyapunov exponents from small data sets[J].Physica D，1993(65):117-134.

[4]GRASSBERGER P，PROCACCIA I.Measuring the strangeness of strange attractors[J].Physica D，1983(9):189-208.

[5]王海燕，卢山.非线性时间序列分析及其应用[M].北京:科学出版社，2006:12-43.

[6]刘晨辉.电力系统负荷预测理论与方法[M].哈尔滨:哈尔滨工业大学出版社，1987:77-112.