时变β系数的卡尔曼滤波的仿真与估计
梅婷,李建勋
0 引言
β系数是度量证券系统风险的一个重要指标,在经典的金融分析中,CAMP中的β系数是假设不变的。大量的实证研究证明,β系数稳定的假设在很多金融股市是无效的,如Australia[1], UK[2]。Brooks[1],Torben G.Andersen[3]等人的研究均支持β值不稳定的观点。随着研究的深入,β的时变性得到广泛的承认。同样国内的文献,如李云翼[4]均表明了β的时变性;王春峰、张亚楠、房振明和李晔[5],吴武清、陈敏和刘伟[6]等支持β的时变性,并对时变CAMP下的理论模型进行建模研究。从直观上判断,宏观经济因素、行业特征、企业自身的因素都会影响β值的变化,换而言之,经济增长率、通货膨胀率、利率水平、特定行业的景气程度、企业自身的会计变量等因素均会通过不同的渠道对β构成影响。因此在对β系数的研究中,时变性是必须加以考虑到重要因素,它不但有利于投资者进行动态组合投资,还有利于投资者构建有效的套期保值策略。
本文对时变的β系数进行研究,通过市场模型描述单个资产收益率和市场组合收益率的关系,假定β系数服从随机行走过程,因为不能对所有的资产收益率成分进行完整的建模,于是给出一个随机模型。在此模型中需要对参数β进行估计,随机变量是高斯分布的,并且方差未知。在估计参数β前,通过极大似然法估计那些未知的参数。由于所有提出的参数都是随机并且高斯的,本文将Kalman filter运用到参数的估计算法中。
1 数学模型
1.1 理论的市场模型
资产收益率和市场组合收益率间的关系可以通过下面标准的市场模型表示:

式中:
Rit为证券i的收益率;
RMt为市场组合的收益率;
ait为证券i的收益率中与组合收益率无关的随机变量;
εit为服从均值为0的高斯分布随机项。方程(1)表明在时间t期间,资产i收益率Rit与同期间的市场组合收益率RMt相关,这两个变量间呈线性关系。系数β是相当重要的一个参数,它表明单个资产收益率怎样随着市场收益率变化,并且可以用来测量资产的系统风险或者市场风险。
1.2 时变参数的状态空间模型(随机游走模型)
状态空间表示一个系统是现代控制论的基本技术,由两个方程构成:一个是状态方程,另一个是观测方程。其中,状态方程表示从目前状态向下一个时刻状态转换的方法,即相互间的转换关系;而测量方程表示实际观测到的自变量和因变量之间的相互关系。
文献中有很多具体的模型来描述系统风险,但是总结起来可以用两个简单方程的模型来表示。大量的研究认为资产定价服随机游走模型。文献[11] ,[12]用大量的篇幅证明β服从随机游走模型。随机游走(RW)模型表达如下。

εit、μit和ηit均是服从高斯分布的。我们根据文献[2]所使用的风险系数的卡尔曼滤波方法,在随机游走模型的回归变量前加上未知的常量F1、F2,于是本文的模型如下所示:


初始条件是:

其中,ф、Q、Q2均是未知的。下面会给出模型的状态空间形式。
1.3 系统方程
由(5)、(6)、(7)我们很容易想到状态空间形式,将a和β作为状态变量,组成一个2×1维的向量,即下面的(11)式所示,于是我们容易得到状态方程和观测方程,分别如下所示。
观测方程:

上面的方程代表时变系数的市场模型。C(t)是T×2维的矩阵,每行代表确定点时间的观测值,我们认为它已知。

状态向量x(t)是2×1维的,包含t时刻的a和β系数:
ε(t)是资产收益y(t)没有建模的一部分,它的方差未知,假设其值有限并且

我们知道,状态方程的一般形式是:

ξt的方差矩阵F是有限对角形式的,对角处因子的值未知。
我们所采用的随机游走(RW)模型中,ψ是一个对角矩阵,

状态噪声的矩阵方差形式:

于是,我们的模型中有 5个参数要估计:ф和矩阵F对角处的因子,也即是状态方程随机干扰项的方差;我们要估计的未知参数向量
2 算法
2.1 模型的最大似然函数
需要估计误差项的位置方差值,参数估计所需要的数据包括单个证券收益率和市场组合收益率。对方程 (9)进行变换,即:

将v0(t)的方差记为ψv0(t),则:


对(20)式两边同取对数,那么最小化的似然函数为:

2.2 卡尔曼滤波及其似然函数
处理标准状态空模型的基本工具是Kalman filter递归算法,它通过t-1时刻状态的最优估计和t时刻的输出给出了t时刻状态向量的最优估计。(其原理和功能是:首先进行模式状态的预报,接着引入观测数据,然后根据观测数据对模式状态进行重新分析(即更新);随着模式状态预报的持续进行和新观测数据的陆续输入,这个过程可以不断向前推进。本文模型的卡尔曼滤波的更新迭代过程如下:
(1).协方差矩阵的预测:

(2).滤波增益

(3).估计协方差阵(更新)

(4).状态向量的预测

(5).状态向量的估计(更新)

参数β值每个时间t的最优估计可以通过提取向量的第二部分得到,即令新息其协方差矩阵则卡尔曼滤波的正态对数似然函数为

参数估计的过程:
1)先利用卡尔曼滤波得到t时刻的新息v(t)与其协方差阵M(t),从而获得了似然函数;
2)将似然函数最大化,得到t时刻的估计值;
3)然后将估计的值代回滤波方程和更新方程,进行滤波和预测,获得t+1时刻的新息与其协方差矩阵;
4)继续循环t时刻的过程,即循环1)、2)、3)的过程,并且依此递推下去。
所以,我们的参数估计过程是卡尔曼滤波与极大似然函数融合的过程,是不可分割的。
应用Kalman filter来估计时变参数的优点在于:首先,计算是递归的,当前的估计是基于过去所有的历史观测,不需要比回归更多的观测或者存储;其次是收敛快。现在已经成为处理标准状态空模型的基本工具,广泛被应用于各种领域。近年来,一些金融计量学家应用Kalman filter及其扩展来探索金融时间序列的动态特征。
3 仿真
3.1 样本数据
我们选择 A股指数作为市场指数。由于实践中很难找到一个接近市场组合的市场指数,国外金融服务机构通常采用标准普尔500指数、纽约证券交易所指数,ilshire5000指数或 Russen3000指数等,而不同的市场指数均导致不同的β估计值。鉴于A股指数发布至今己为计算市场收益率提供了大量基本数据,且实践表明 A股指数能够较为准确地反映整体行情的变化和股票市场的整体发展趋势,比较符合CAPM所描述的市场组合。因此,本研究选择A股指数这一价值加权指数,符合CAPM市场组合构造的要求。
本文选取 Wind行业指数中一级行业指数作为数据样本,Wind行业指数成分股仅包含A股股票,包括能源指数、材料指数、金属指数、工业指数、可选消费指数、日常消费指数、医疗保健指数、信息技术指数、电信服务指数和公用事业指数10个行业的指数。选取沪市2001年8月——2006年10月作为研究的时间段。对于以上数据的选取,我们解释如下:尽管股票市场始于 1990年,但上市之初一方面股票数量较少,不满足统计分析的需要;另一方面股市法规不健全、市场体制不完善,大多数投资者不具条理性投资者的特点,因而分析和检验所选用的历史数据不能从创市之初算起。我们截取2001年8月到2006年10月的交易数据作为研究的对象,其间我国股市运作已基本正常,约束法规已较为健全,交易和投资活动日趋理性,投资者的心态也较为平稳。
3.2 收益率的计算与初始值
对于模型的待估参数的初始值,我们是通过滚动最小二乘法来获得的(rolling OLS),由于滚动回归比真实的模型噪声大很多,对于大多数的系数的值为按照由OLS方法所得系数的一半来计算。
3.3 预测方差
我们采用两个指标对模型的优劣进行评价,两个指标是针对模型的预测精确度所设计的:平均平方预测误差 MSE和平均绝对预测误差MAE,计算公式分别如下:

3.4 仿真结果比较与分析
一般来说,β值描述了证券收益率对市场投资组合收益率的标准差的边际贡献。通过对 β值大于、小于或等于 1的描述我们可以看出该证券的收益率是趋向于放大、缩小或等于市场投资组合整体的收益率。β系数描述了股票的收益和风险状况。我们希望积极型或者说高杠杆率的公司的风险系数高些,而那些一般市场行为对公司行为影响不大或没有影响的公司风险系数低些。
我们是利用MATLABR2007a来进行估计和仿真的。当F1、F2均未知时,模型参数的估计结果如下面表1所示;当F1=1,F2未知时,模型参数估计的结果如表2所示。

表1 模型参数估计结果、MAE和MSE
下面为表1的续表:

行业 F1 F2 MAE MSE能源 -0.17335 1 0.0105 2.3438e-04材料 0.19249 0.99986 0.0064 8.7215e-05工业 0.55003 0.99996 0.0071 1.0441e-04可选消费 0.18144 0.99997 0.0088 1.5078e-04日常消费 -1 0.99843 0.0109 2.2306e-04医疗保健 1.0166 0.95371 0.0122 2.8955e-04金融 0.09413 0.99927 0.0109 2.1938e-04信息技术 -0.3445 0.99997 0.0140 3.6479e-04电信服务 0.05835 0.98949 0.0147 4.8780e-04公用事业 -0.10273 1 0.0081 1.3747e-04

表2 F1=1时模型参数估计结果、MAE和MSE
表2的续表如下所示:

行业 F2 MAE MSE能源 1.0211 0.0115 2.7237e-04材料 0.99792 0.0075 1.3595e-04工业 0.98344 0.0082 1.5025e-04可选消费 0.99576 0.0097 1.8032e-04日常消费 0.99455 0.0115 2.4411e-04医疗保健 0.99289 0.0120 2.7977e-04金融 0.99571 0.0112 2.3389e-04信息技术 0.51055 0.0214 7.9545e-04电信服务 0.99365 0.0148 4.8950e-04公用事业 1.0002 0.0090 1.6009e-04
比较表1与表2,我们发现表1中预测误差明显低于表2中的预测误差,而两表中F2的值均近似为1;也即对于随机行走模型,风险系数β是适合的,而模型中关于α的方程引进未知参数F1是合理且更优的。
β系数的仿真图、行业拟合预测的序列与实际序列的比较图均如下10幅图所示。从β的仿真图容易看出金融行业的风险系数较高,而且变化幅度也大,这是与行业特征相关;电信服务因为从2002年10月份才开始,所以前面一段为0;而波动幅度也是与市场需求和业务发展有关。能源行业、可选消费和公共事业几个行业的需求弹性比较小,所以这几个行业的风险系数变化得比较平缓。纵观拟合曲线与序列的真实曲线,通过表1中平均平方预测误差MSE和平均绝对预测误差MAE值可看出,医疗保健、金融行业、信息技术行业和电信服务行业误差比较大,因为我国近年来随着经济的发展,电信、医疗保健、金融市场和信息技术都发展得比较快,行情不稳定,由此可以看出我们所选的模型方法是比较符合现实的。10幅仿真图分别如下所示:
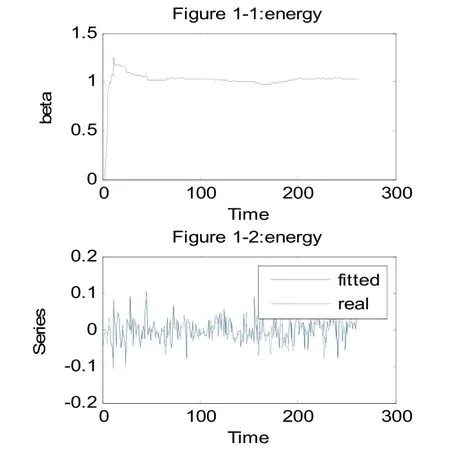
图1 能源行业风险系数、拟合预测序列与实际序列图

图2 材料行业风险系数、拟合预测序列与实际序列图
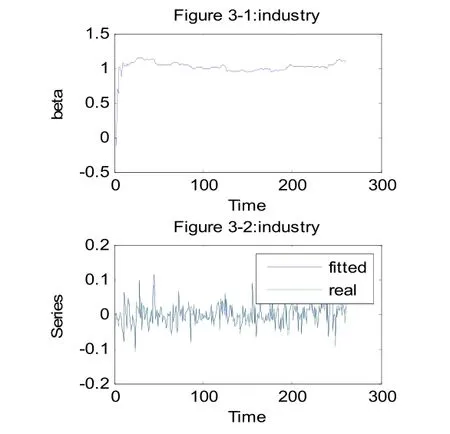
图3 工业风险系数、拟合预测序列与实际序列图

图4 可选消费行业风险系数、拟合预测序列与实际序列图

图5 日常消费行业风险系数、拟合预测序列与实际序列图

图6 医疗保健行业风险系数、拟合预测序列与实际序列图

图7 金融行业风险系数、拟合预测序列与实际序列图

图8 IT行业风险系数、拟合预测序列与实际序列图
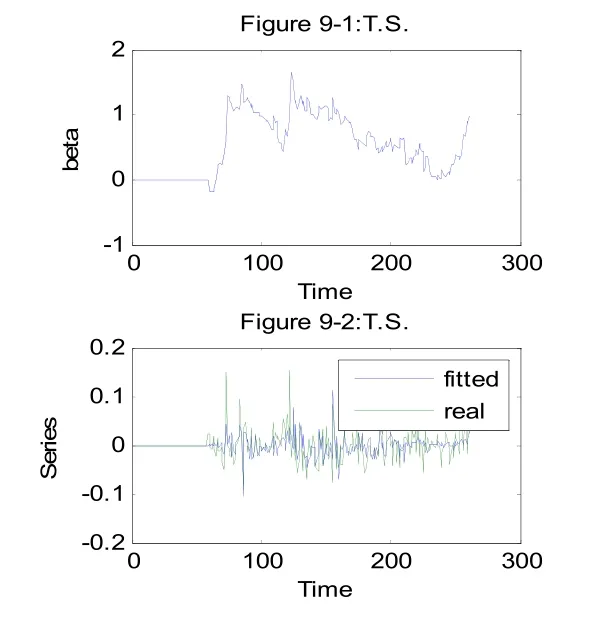
图9 电信服务风险系数、拟合预测序列与实际序列图

图10 公用事业风险系数、拟合预测序列与实际序列图
由以上分析可知,上海行业股票组合的系统风险系数β是不稳定的,存在时变性。至于β的行为特征,上海行业股票组合系统风险系数β的时变行为用随机游走模型来描述是恰当的。这一结论同时表明,对上海当前的股票市场,不能采用恒定的β系数进行模拟;若知β系数的时变性行为特征,就可以对条件β系数进行预测,从而可以利用CAPM进行投资组合和业绩评价。
4 结论
资产的系统风险由于一些微观因素和宏观因素,会随时间而变化。本文旨在预测风险系数,我们对沪市10个行业的β系数的时变行为采用随机游走(RW)模型,在随机游走模型的回归变量前引进了未知参数,仿真预测的结果表明,引进未知系数后的模型,其绝对预测误差MAE和均方预测误差MSE都比引进未知系数前的模型更精确,改后的模型更适合描述沪市行业风险系数的时变行为。仿真过程是通过卡尔曼滤波的递推过程获取新息及其协方差阵,得到似然函数,从而推进参数估计。将估计的结果返回卡尔曼滤波更新过程,易得观测变量的预测值。β的研究很重要,本文是采用卡尔曼滤波的方法来处理时变风险系数改进的模型;而计量经济学、时间序列技术的各种工具以及最新进展都会为β值的研究提供新的思路和新的视角,以基金为代表的机构投资者必定会有越来越多地关注β的研究。
[1] Brooks R D, Faff R W, McKenzie M D.Time-varying beta risk of Australian industry portfolios: A comparision of modeling techniques[J] . Australian Journal of Management, 1998, 23(1):1-22.
[2] Black A,Fraser P. & Power D.UK unit trust performance 1980–1989: A passive time varying approach[J] ,Journal of Banking and Finance, 1992,16 (10):15-33.
[3] Torben G Andersen, Tim Bollerslev,Francis x Diebold,Jin(Ginger)Wu.A framework for exploring the macroeconomic determinants of system risk [D] .Working Paper, Northwestern University,2005
[4] 李云翼.股指期货背景下对 β系数的重新审视[J] .科技信息,2008,(25).
[5] 王春峰,张亚楠,房振明,李晔.中国股市已实现 β系数的特征分析与建模研究[J] .北京理工大学学报(社会科学版),2008, 10(1).
[6] 吴武清,陈敏,刘伟.中国股市时变贝塔的统计特征及其在股指期货中的应用[J] .系统工程理论与实践, 2008,10:1-2.

