基于视频的车型特征提取及识别方法研究

王慧斌，芦蓉

0 引言

车型识别作为 ITS中的一个重要分支，在打击盗窃车辆、规范交通秩序、大型停车场管理、高速公路自动计费、交通流量统计等方面具有广阔的应用前景[1] 。由于视频图像中包含的信息内容丰富，因此，基于视频图像而进行的车型识别技术相较于其他监测技术而言更具有应用优势。同时，也还存在一些问题迫切需要解决。一方面是计算的复杂性问题。这是由于车型识别包含诸多的处理环节（如，车辆检测、车型特征提取等）流程，且在处理的各个环节采用了多种方法，因此如何简化使得处理更加高效非常重要；另一方面是识别对象的复杂性问题。由于交通场景多变，车辆类型多样，以及车辆移动造成的变化等，增加了车型识别难度。因此，如何解决这些问题已成为车型识别研究的重要内容。

目前主流的车型识别技术主要是基于统计模式识别的方法[2] ，该方法的流程见图1所示：

统计模式识别就是在已知训练样本集的基础上设计分类算法，并进而对未知样本进行辨别分类。分类算法是基于对训练样本向量学习的，因此其计算的复杂度和样本特征的维数密切相关，其分类的准确度和样本特征的鉴别性能密切相关。可见，基于统计模式识别的方法中，特征选取是其关键问题

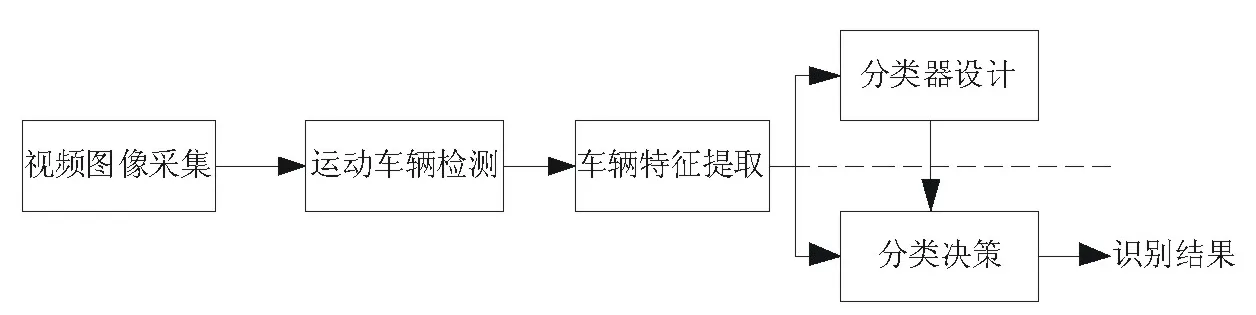
图1 基于统计模式识别的车型识别流程

本文的车型识别方法选择车辆图像的灰度矩阵作为初级描述特征，并采用基于子空间分析的特征提取优化方法PCA-LDA，对初级特征进行优化处理。在此基础上进一步设计了一种1-V-1 SVMs车型分类器，并结合KNN方法来进一步提高识别的准确率。

1 车辆特征提取优化方法

1.1 车型特征提取方案

目前大部分的车型识别所选择的识别特征都是如车体的轮廓、车长、车高、面积和轴距等几何数据[3,4] 。而在实际应用中，车辆直观性特征的准确提取依赖于对运动车辆检测的精度，然而，车辆精确检测本身就是较为复杂的问题。同时，直观性特征又较难反映车型的细节变化。考虑到车辆的灰度图像较易获得且含有较多有效信息的。因此，本文采用车辆图像灰度矩阵作为车型的初级描述特征。然而灰度特征的维数很高，特征数据之间的冗余大，不利于计算，因此需要进行“二次特征”的提取，从而获得一组有利于学习和分类的“少而精”的目标特征用于识别。

“二次特征”提取的实质是通过空间变换得到车辆的识别特征。这些特征要能够满足有效、冗余减少以及降维等要求。因此，本文设计了一种基于PCA-LDA的二次特征提取优化方法，以提取更加有利于学习和分类的车型识别特征。

1.2 PCA-LDA特征提取优化方法

PCA（Principle Component Analysis）[5,7] 是一种多元统计数据分析方法，其基本思想是通过线性变换，将高维空间的问题转换到低维空间进行处理。它能够去除原始特征间的相关性，同时保持原始空间数据所提供的大部分信息，该方法具有很好的降维性能且丢失的数据信息最少，得到的特征能够很好的代表原始数据但并不具有鉴别能力；LDA（Linear Discriminant Analysis）[6,7] 是一种用于判别样本所属类型的统计分析方法，它把高维数据投影到一个低维空间中，并且尽量使得在此低维空间中，同类样本点聚集在一起，而不同类的样本点分开。它能在降维的同时考虑到原始数据不同类别间的分类特征，从高维特征空间中提取出最具有鉴别能力的低维特征，但是对在实际中普遍存在的小样本问题，其类内散布矩阵经常是奇异的。

本文设计的 PCA-LDA特征提取优化方法结合了 PCA和LDA各自的优点，首先通过PCA方法将高维图像空间压缩至主成分向量张成的低维PCA子空间从而消除特征数据的奇异性，然后在此空间中再通过加权LDA方法提取最佳鉴别特征。通过该方法获得的车型识别特征维数低、鉴别性能高，因此分类器的计算快速、准确率高，取得了较好的识别效果。

PCA-LDA方法的特征提取流程如图2所示：

图2 PCA-LDA方法的特征提取流程

其具体实现过程如下：

（1）把每幅图像对应的灰度矩阵按照行或者列的形式展开成一个向量。这些向量构成一个矩阵X，每一行代表一个样本，每一列代表一个特征值。

计算矩阵X的协方差矩阵R：

式中的μ是样本的总体均值向量，R是通过求矩阵的期望得到的。通过解特征方程，得到R的p个按照降序排列的特征值iλ及相应的正交归一特征向量取累计贡献率达到的前k1个主成分，得到k1个主成分张成的特征空间W1。

（2）将所有训练图像都投影到W1空间中，得到投影后的最佳描述特征。然后利用加权LDA方法计算图像最佳描述特征的类内散布矩阵Sw和类间散布矩阵sb。

假设共有c类样本，Pi是每类样本的先验概率（实际中，先验概率Pi往往等于类ωi的样本数与总体样本个数的比率），μi是第Ci类样本的均值，μ是所有样本的均值，Xi是属于第i类的样本。类内散布矩阵Sw和类间散布矩阵Sb见式（2）和式（3）：

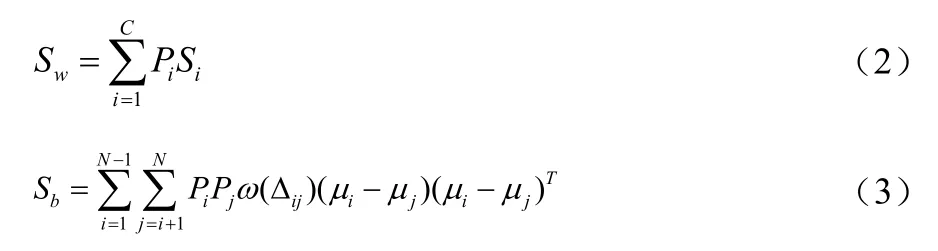
（4）求出W=W1*W2，W就是图像的最佳投影矩阵；

（5）通过最佳投影矩阵，获得所有训练图像的最佳分类特征。

2 基于支持向量机的车型识别

2.1 支持向量机

支持向量机（Support Vector Machine, SVM）方法[8] 是一种基于统计学习理论的模式识别方法，其主要思想可以概括为两点：（1）它是针对线性可分情况进行分析，对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分；（2）它是基于结构风险最小化理论在特征空间中建构最优分类超平面，使得学习器得到全局最优化,并且在整个样本空间的期望风险以某个概率满足一定上界。

设有样本xi和它的分类yi，表示成是输入空间的维数。对标准化SVM，它的分界面是其最优化问题可以用下面的二次规划问题表示：

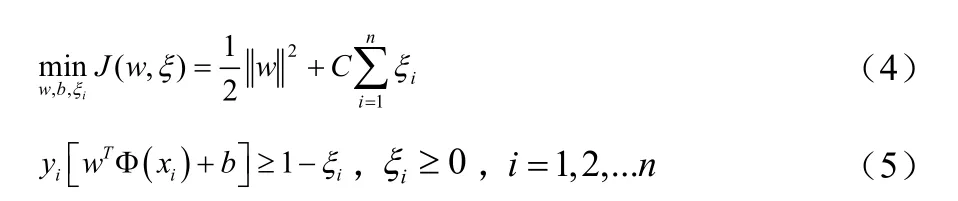
ξi≥0（i=1,…N）是一个松弛变量，用来保证对线性不可分数据的有效分类。参数C是一个正常数，称为惩罚参数，是对经验风险和表达能力的一个裁决。C越大表明对错误分类的惩罚越大。函数 ф是一个非线性映射函数，用于把数据映射到高维空间，但是它并不是显性结构函数。通过转换空间，我们得到最优超平面。

在构造最优超平面时，训练算法只涉及到空间中的内积运算，即可以采用满足Mercer条件的核函数来代替该内积运算，目前主要的核函数有：

（3）RBF（径向基）核函数：

2.2 车型识别分类器设计

由于在实际中所获得的车辆训练样本有限，因此本文采用在解决小样本、非线性及高维模式识别问题中表现出了很多特有的优势的SVM方法来进行分类识别。

假设对小轿车、卡车和客车三类车型进行分类。这是一个多类分类问题。在SVM的分类策略中[9] ，利用“一对一”方法构造的组合分类器泛化能力较强，在实际应用中能够获得比较高的分类精度，因此本文就采用这种构造策略来构造车型识别分类器1-V-1 SVMs。

设三种车型分别为ω1、ω2、ω3，类别数N=3。每类的样本数为n1，n2，n3，总样本数=n1+n2+n3。第i类和第j类之间的子分类器SVMt对应的训练样本是ωi和ωi（i≠j，i=1,2,3，j=1,2,3，t=1,2,…,N(N-1)/2），每个子分类器采用SVM算法对训练样本集进行学习，其最优化问题如式所示。通过学习，求出每个子分类器对应的支持向量、最优分类面的系数及常数b等。

2.3 基于KNN-SVM的分类决策

SVM子分类器可以看做每类只有一个代表点的1NN分类器[10] ，它对每类只取一个代表点，如果该代表点无法很好的代表该类，那么分类结果就会出现错误。而KNN方法将每类所有的支持向量都作为代表点，对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

对SVM分类时错分样本的分布进行分析发现，其出错样本都在分界面附近。针对这种现象，为了进一步提高识别率，本文在子分类器中结合使用了SVM和KNN两种方法进行分类决策。KNN-SVM 方法的分类思想是：当样本距SVM 最优超平面的距离大于一定阈值ε即样本离分界面较远时，用SVM方法进行分类；反之即样本离分界面较近时，用KNN方法对样本进行分类。ε一般设定为0～1之间的常数，可以看出当ε=0时，就仅用SVM算法进行分类。具体分类过程如图5所示：

引入KNN算法不会增加SVM算法的时间复杂度，而且能减少SVM分类超平面附近样本点的错分率，从而提高分类器的准确率。

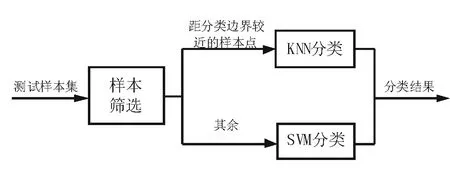
图3 KNN-SVM方法的分类过程

设测试样本集为T，由训练得到的支持向量集为Tsv，k是KNN算法中最近邻的个数。KNN-SVM分类算法伪代码如下：

Step1: 如果Φ≠T，取Tx∈；否则，停止；

Step4: 从测试样本集中减去样本x即TxT→−，回到步骤1继续。

其中，Step3中使用的KNN算法是将支持向量集Tsv作为分类算法的代表点集合的，且其计算测试样本和每个支持向量的距离都是在特征空间中而不是原始空间中进行的，因此其使用的距离公式不能采用欧式距离公式，而是采用如下公式：

基于KNN-SVM的分类决策过程如图4所示：

图4 KNN-SVMs的决策过程

对所有子分类器的输出结果利用投票法进行统计。投票统计的过程是：计算关于i类的子分类器分类结果，判断测试样本x是否在第i类：若在，则给第i类的票数加1。用同样的方法遍历所有类最后比较每个类所得的票数，把测试样本x归类到票数最多的那类去。

3 实验分析

3.1 数据准备

实验中，所采集数据是车道上的车辆的侧面影像。然后通过运动车辆检测算法从交通视频序列中定位分割出车辆目标。最后将所分割出的车辆目标图像的大小全部转化为160*50（长*宽），就是本文所使用的标准车辆图片。选取30幅车辆图片（共 3类，每类 10幅）作为训练样本，15幅车辆图片（共3类，每类5幅）作为测试样本集1，将此测试样本中的车辆图片分别作旋转、颜色调整、放大以及加入噪声等变换，扩充测试样本集的样本数目到 30，得到测试样本集 2、3、4、5。车辆图像四种变换的效果如图5所示：

图5 车辆图片四种变换效果图

3.2 实验仿真

分别提取30幅训练样本集的PCA、PCA-LDA特征，其维数变化如表1所示：

表1 特征的维数变化

原始特征是车辆的灰度矩阵，转换成向量形式后其特征维数为160*50=80000。分别用PCA方法和PCA-LDA方法进行二次特征提取，获得的特征维数都大大降低，且PCA-LDA的特征维数仅为2。因此，在二维坐标系中用横、纵坐标分别表示特征的第一、第二维数据，30幅训练样本的分布情况如图6所示：

图6 训练集样本分布图

从图6中可以观察到，训练样本集的分布符合不同类样本点之间远离，同类样本点之间靠近的规律，可见PCA-LDA特征有很好的鉴别性能。

本文的子分类器使用C-SVM算法，核函数选取相对比较稳定的高斯核函数惩罚因子 C和高斯核函数参数σ的选择采用交叉验证的思想，在 [2-10,210] 范围内进行参数寻优。分别对测试集1、2、3、4、5进行分类，结果如表2所示。

表2 车型识别结果

从表2可以看出，经过PCA-LDA特征提取优化方法所提取的车型识别特征对车辆的变形、颜色变化、噪声干扰都有较好的鲁棒性，且识别率较高。

表3是车型识别速度。从表3中可以看出，经过二次特征提取后获得的识别特征，无论是PCA特征还是PCA-LDA特征，由于其维数大大降低，因此其分类识别的速度也有了大大提高。特别是PCA-LDA特征在分类识别率和识别速度方面都有很好的表现。

表3 车型识别速度

4 结论

本文采用了基于统计模式识别的车型识别方法，在车型特征提取时，充分利用了LDA方法能够获得最佳鉴别特征的优势，提出了一种基于PCA-LDA的特征提取方法。同时，采用“一对一”策略构造了车型分类器1-V-1 SVMs，并基于KNN方法提高SVM子分类器分类准确率。实验仿真结果证明了本文方法的有效性。

[1] Broggi A, Vehicles S. Intelligent Transportation Systems[C] . Citeseer, 2008: 2-7.

[2] Clady X, Negri P, Milgram M. Multi-class vehicle type recognition system[J] . Artificial Neural Networks in Pattern Recognition, 2008, 228-239.

[3] Fujiyoshi H,Kanade T. Algorithms for cooperative multisensor surveillance[J] . Proceedings of the IEEE,2001, 89(10):1456-1477.

[4] 袁志勇,查桂峰,陈绵云,张仁宏.基于反对称小波的车型识别研究.武汉大学学报,2005,30(6):560-563.

[5] Chengcui Zhang, Xin Chen,Wei-bang Chen.A PCA-based Vehicle Classification Framework [J] . IEEE International Conference on Data Engineering Workshops, 2006:17-26.

[6] 郭娟,林冬,戚文芽.基于加权Fisher准则的线性鉴别分析及人脸识别.计算机应用,2006,26(5):1037-1039.

[7] Peter N, Belhumeur, Joao P. Hespanha, and David J.Kriegman. Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997,19(7):711-720.

[8] Cui B,Xue T,Yang K. Vehicle Recognition Based on Support Vector Machine[C] . International Symposium on Intelligent Information Technology Application Workshops, 2008:443-446.

[9] Gou B,Huang X.SVM multi-class classification [J] . Shuju Caiji yu Chuli(Journal of Data Acquisition & Processing,2006, 21(3):334-339.

[10] 李蓉,叶世伟,史忠植. SVM—KNN分类器:一种提高SVM分类精度的新方法[J] .电子学报,2002,30(5) :745-748.