选课系统的资源最优化分析

黎红

0 引言

随着我国教育体制的发展，高校中采用完全学分制的院校越来越多，在学分制高校中，选课是学校教学活动的不可缺少的重要一环。选课的顺利实施，对于学校的决策者和管理者以及学生来说都至关重要，所以高校选课系统应该能够高效、顺利地解决学分制，特别是完全学分制高校的选课问题，选课系统需要面临的主要问题，不是系统的开发难度，而是服务器以及网络资源的最优化。

大多数的学分制或完全学分制院校，学生所上的课程全部由学生自主选定，而学生感兴趣的课程和上课时间出现大量的冲突，导致学生在网上选课开放的时间内，由于大量同时登录系统，造成系统服务器的资源极度紧张，服务器负荷严重超载，有的学生几个小时都无法登录系统，造成选课极不顺利。如果要增加服务器以缓解资源的紧张，但是这样势必会造成投资方的成本增加，甚至出现因供大于求而使设施经常闲置，导致浪费，因此需要一个合理的算法，通过分析处理系统的状况，对系统进行调整和改进，以确定最优的服务器数量和学生网上排队人数，在把排队的时间控制在一定限度的前提下，使服务器质量的提高和成本的降低之间取得平衡，找到最适当的解决方法，使系统处于最优的运行状态。

1 排队模型的简介

目前传统采用的排队模型和算法，多为服务器数量为1的单通道损失制系统的排队模型，或单通道等待制系统的排队算法。目前单通道的排队算法可用图1来表示：

图1 单通道排队的一般模式

排队的规则有损失制、等待制和混合制，等顾客（学生到达时，若所有服务器均被占用，该顾客离去，这种排队规则称为损失制或即时制。这种情况在选课时出现机会不大，因为大多数心急如焚的学生会选择长时间的等待，甚至通宵达旦地选课；当顾客到达时，若所有服务器被占用，顾客并不离去，而是排队等待服务，这种排队规则称为等待制。而将二者进行结合则称为混合制。而在这3种规则中，当服务器的数量为1(单一服务器系统)时，称为单通道损失制或单通道等待制。目前国内外大都以此种方式来处理选课的排队问题，这种传统的方法在一定程度上缓解了选课的压力，当学生人数过多时，采取限制学生人数的方法，以保证单一的服务器能正常运作。但是随着高校近期的扩招，在校高校人数近几年激增，单一的服各器的选课系统，已无法满足日渐增加的选课学生人数，造成选课系统效率低下，甚至几近瘫痪。

多通道的排队机制则采用多台服务器并行处理选课请求，由于近几年硬件价格的下调，使一般高校购入多台服务器成为可能，从多购入一台服务器便可大大减少学生等待的时间和等待的人数上说，是符合选课系统的效益的；但是无节制地增加服务器也是不符合经济效益的，因为毕竟选课只是高校管理中一个短暂的过程，大多数时间内让太多的服务器闲置，势必会引起投资方的不满，也是对资源的浪费。因此在保证学生不因服务器过忙而失去信心离开的情况下，采用等待机制，而不是损失制的排队模式，并且采用多服务器的多通道等待排队机制，是解决目前高校选课系统中资源和请求人数的冲突的瓶颈的最好方法。

2 多通道等待排队算法的模型

多通道等待排队模型又称多服务台等待制M/M/C排队模型,即 M/M/C/,顾客来到的时间间隔服从参数的负指数分布，服务员为顾客服务时间服从参数的指数分布，C个服务台，系统容量为的等待制排队模型。

2.1 稳态的概率分布

M/M/C/模型系统状态图为

因此在前面生灭过程微分差分方程组式中，令

得到此模型微分差分方程组

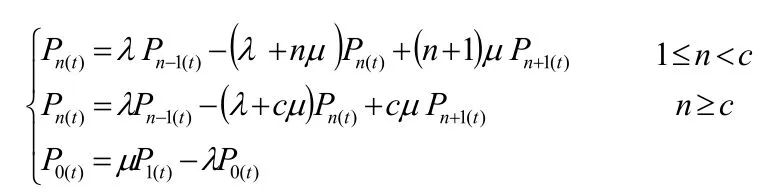
2.2 列出各状态的代数方程

令 ρ=λ/µ, 因为 ρ/n <1 系统状态极限概率存在,根据生灭图和建立柯尔莫可洛夫方程的一般法测,有：

对 S0 有: λP0=µP1P1=(λ/u)P0=ρP0

对 S1 有: λP1=2µP2P2=(ρ2/2!)P0

对 S2 有: λP2=3µP3P3=(ρ3/3!)P0

…

对 Sn-1 有: λPn-1=nµPn Pn=(ρn/n!)P0

…

对 Sn+r-1 有: λP n+r-1=nµP n+r Pn=(ρn+r/nr*n!)P0

由正则条件：

P0+P1+P2+…+Pn+m=1 可得出系统的效率指标公式。

2.3 排队选课系统的效率指标的求解

根据 P0求出系统的效率指标：系统损失概率、系统的相对通过能力、系统的绝对通过能力、系统内排队的等待选课的学生平均数、学生的平均排队等待时间、占用服务器的平均数、系统内的学生平均数。

以上各项指标如下：

（1）系统损失概率

在等待系统中，请求服务的顾客迟早会被接受服务，所以，P损=0

（2）系统的相对通过能力

Q=1-P损=1

（3）系统的绝对通过能力

A=λQ=λ

（4）系统内排队的等待选课的学生平均数

顾客的平均排队时间

W队==ρnP0

（6）系统内顾客平均数：L系=L队+ρ

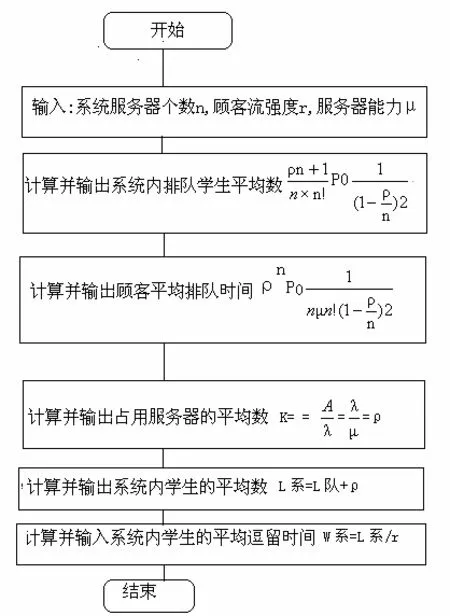
2.4 多通道等待排队算法实现的程序流程图

以上算法是根据前面的分析，得出的公式而推导出来的，用Pascal语言不难得以实现。

3 结束语

多通道的排队机制则采用多台服务器并行处理选课请求，由于近几年硬件价格的下调，使一般高校购入多台服务器成为可能，以多购入一台服务器便可大大减少等待的学生时间，和等待的人数上说，是符合选课系统的效益的，但是无节制的增加服务器也是不符合经济效益的，因为毕竟选课只是高校管理中一个短暂的多程，大多数时间内让太多的服务器闲置，势必会引起投资方的不满，也是对资源的浪费，因此在保证学生不因服务器过忙而失去信心离开的情况下，采用等待机制，而不是损失制的排队模式，并且采用多服务器的多通道等待排队机制，是解决目前高校选课系统中，资源和请求人数的冲突的瓶颈的最好方法。

[1]陈付龙,樊晓桠.利用排队论分析嵌入式多任务系统的性能[J].计算机工程与应用,2006,36:4-6.

[2]廖亚红.运筹学排队论在客户服务中的应用与辅助决策[J].商场现代化,2006,485:20-21.

[3]林闯.计算机网络和计算机系统的性能评价[M].北京:清华大学出版社,2001,127-230.

[4]郭耀煌.运筹学原理与方法[M].成都:西南交通大学出版社,2000:231-255.

[5]陈明.信息与通信工程中的随机过程[M].上海:科学出版社,2005.7-123.

[6]林齐宁.运筹学[M].北京:北京邮电出版社,2003.25-46.