峰谷分时电价决策的优化模型

郜 璘，周国祥，石 雷

（合肥工业大学 计算机与信息学院，合肥 230009）

0 引言

为缓解电力紧张的局面,目前国内外普遍实行需求侧管理 (demand side management,DSM)这一有效的调节手段，通过价格信号引导电力用户采取合理的用电结构和用电方式，形成比较平稳的电力负荷状态[1]。安徽等省份采取的峰谷分时电价即为一种有效的DSM措施，是供电公司为实施DSM而向用户提供的一种经济上的刺激手段。所谓峰谷分时电价 (peak and valley time-of-use electricity price,TOU)就是供电公司根据电网的负荷特性确定峰谷平时段，根据不同时段确定不同的销售电价[2]，通过提升用电高峰期的电价、降低用电低谷期的电价来从经济上激励用户改变用电方式，从而缓解高峰期的用电紧张状况，挖掘低谷期的用电需求,因此采取峰谷分时电价可以达到削峰填谷的目的[3]。用户对于峰谷分时电价响应行为的建模是其定价决策的前提和基础。

在实际应用中，尚无一种公认的峰谷分时电价的制定方法和时段的划分准则。本文在参考相关文献的基础上，将采用基于消费者心理学原理、电价理论及统计学原理，提出以目标为导向，以人为中心，以成果为标准，针对电力企业渴望达到的预期目标值，给出数学模型，并对其进行优化，最终求得最优解。

1 用户响应行为

影响用户某一时刻的用电量有很多因素，一般说来，与此时的电价、天气情况、生产状况、班制、经济政策等因素关系密切。但是从实际可操作性和目标管理的角度出发，电价是较好的控制对象，因此，在分时电价的用户反应模型中将电价作为主要因素加以考虑，而将其他一些宏观因素或暂时无法衡量的因素进行简化[4]。

根据消费者心理学原理，对用户的刺激有一个最小可觉差（差别阈值），在这个差别阈值的范围内，用户基本上无反应或反应非常小，即不敏感期（相当于死区）；超过这个差别阈值的范围时，用户将有所反应，且与刺激的程度有关，即正常反应期（相当于线性区）；用户对刺激也有一个饱和值，即反应极限期（相当于饱和区）[5]。因此，用户对电价的反应可以形成一条用户的反应曲线，本文将采用文献6的电价综合反应曲线对其进行拟合。

假设现行的峰谷分时电价的平时段售电电价为pp，以它为标准值，实施新的峰谷分时电价后用标准值表示，那么，谷段电价用xg表示，平段电价用xp表示，峰段电价用xf表示。为了计算方便，其中取xp=1，监管部门可根据当地的实际情况来确定xg、xf的取值范围。用户的反应曲线可表示为：

2 峰谷分时电价的数学模型

2.1 分时电价模型

实行分时电价的主要目的是为了削峰填谷，减小峰谷差，其目标函数可表示为：

（1）最小化系统峰负荷：

（2）最大化系统谷负荷：

（3）最小化日负荷峰谷差：

其中，Qt(t=1,2,3,…T)分别为实施分时电价前各时段的用电量，T为划分时段的总数。从目标函数来看，这三个函数只选取两个就可以了，取（1）、（2）即可。

约束条件：

（1）实施方获利：实施峰谷分时电价后，实施方的收入应不少于未实施分时电价前的售电收入。

式中，M1为实施TOU后的售电收入，m0为实施TOU前的售电收入，M'为实施TOU后所节约的容量投资费用。

（2）用户受益：实施峰谷分时电价后，应保证用户的购电费用不增加，这也是实行峰谷分时电价的原则之一。

（3）用电总量不变：根据国内外需求侧管理的经验，实行峰谷分时电价后，一般用电量略有增加或基本保持不变，因此,此假设是合理的[7]。

（4）峰谷分时电价的约束：根据监管部门的要求，峰谷差的范围应为2～5倍之间，这是充分考虑了发电成本和用户的承受能力的。

由于供电企业节约的电力投资M'不易估计，如忽略不计，则约束条件（4）、（5）就变成了等式约束，对此文献7给出了充分的说明，本文亦做相同处理。

3 模型的求解

设 Qf、Qp、Qg、Qf'、Qp'、Qg'为实施峰谷分时电价前后的各时段的用电量，由于假设电价前后的用电量不变，根据式（6）、（8）则：

k为实施分时电价后峰时段用电量与谷时段用电量之比，为供电公司提出的期望值，k值越小表示用户用的峰时电越少，同时，k值变化量越小，越利于企业进行负荷调节。这为调节夏冬季用电高峰，改善负荷曲线，有很好的启示，对于企业实施目标管理亦有很大的帮助，给定k后，xf、xg可有多组解。

假设电价综合反应曲线函数如下[6]：

优化过程如下：

对单目标分别进行优化，首先，以求解最大负荷最小值为目标，得出此时的最优电价为：xg,xp,xf和目标函数的最优值Lmin；其次，以峰谷差最小化为单目标的优化结果为：xg',xp',xf'及目标函数的最优值dmin，最后根据理想点法求xg*,xp*，xf*，这样可以使多目标问题转化为单目标问题。

4 仿真计算

以安徽省某企业（大工业用户）为例，峰谷时段划分如下：峰时段为 9：00～11：00 和 18：00～22：00（6 小时）；平时段为 8：00～9：00 和 11：00～18：00（8 小时）；谷时段为 22：00～次日 8：00（10小时）。安徽省现价策略为：峰段电价：0.8958元/kwh;平段电价：0.6020/kwh；谷段电价：0.3747 元/kwh，xf:xp:xg=1.49:1:0.62，本文将此作为初值，运用MATLAB的fmincon函数对模型进行优化。

4.1 原始数据

典型日负荷曲线数据如表1。

表1 典型日负荷数

从表1可得：Lmin=202MW，Lmax=447MW，d=245MW，高峰电量与低谷电量的比值是0.8916。

4.2 优化结果

k可由供电公司历史负荷缺口得出，根据不同的DSM目标，k可取不同的值，并设定不同的约束条件，本文旨在保证供用电双方利益的情况下，尽可能使曲线平滑，故假设k≤0.7。

首先以最大负荷的最小化为目标，可得xg=0.6229，xp=1，xf=1.2625和Lmin=415.601MW；其次以峰谷差的最小化为目标，可得 xg=0.5663，xp=1，xf=1.3036和 dmin=194.3939MW。根据理想点法可得：xg*=0.6211，xp*=1，xf*=1.2652，此时，最大负荷为415.9444MW，最小负荷为226.4711MW，峰谷差为189.4733MW。其日负荷曲线图如图1所示。

实施新的峰谷分时电价后系统最大负荷减少了31.0556MW，峰谷差减少了55.5267MW，日曲线有了一定的改进，变得平滑，最大负荷有了明显下降，峰谷差有了一定的减小。供电公司在实施现有峰谷分时电价的收益为4401.85元，实施新的峰谷分时电价的收益为4424.72元，增加22.87元；用户实施现有峰谷分时电价的单位电价为，实施新的峰谷分时电价的单位电价为0.5589元/kwh，减少了0.0229元/kwh，实现了双方共赢，对于提高电力系统的稳定运行和经济水平具有很大的帮助。

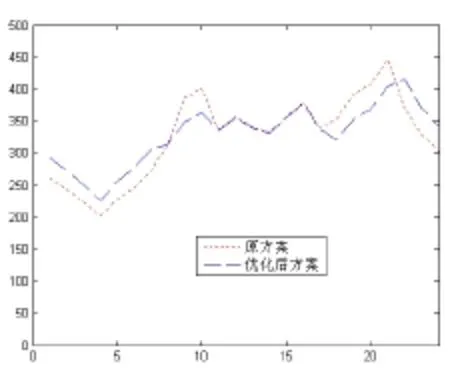
图1 日负荷曲线图

5 结束语

本文介绍了峰谷分时电价的社会意义及峰谷平时段的划分方法，在结合用户反应模型的基础上得出求解方法，并对算例进行了仿真，得出适合的峰谷平时段电价。从中可以看出，在大量掌握了用户对电价差的反应后，根据用户的不同反应度，供电公司可通过主动制定预期目标，再通过模型求解出方案，比单纯对模型优化更合理更具实际意义，符合现代企业目标管理原则。

本文只着重研究电价对用户的影响，简化或忽略其他因素，而在实际应用中，还应综合考虑各方面因素，以求得出更好的方法，促进此项措施的实施，真正做到削峰填谷，使电力企业和用户达到双赢。

[1]Roos J G,Lane I E.Industrial Power Demand Response Analysis for One-part Real-time Pricing[J].IEEE Trans on Power Systems,1998,13(1).

[2]Kischen D S,Strbac G,Cum Perayot P,et al.Factoring the E-lasticity of Demand in Electricity Prices[J].IEEE Tans on Power Systems,2000,15(2).

[3]吴秋伟,汪蕾,程浩忠.削峰填谷最优时基于DSM分时电价的确定与分析[J].继电器,2004,32(3).

[4]刘严,谭忠福,张艳红.探析我国分时电价设计的相关问题[J].价格理论与实践,2005,(6).

[5]罗运虎,邢丽冬,王勤等.峰谷分时电价用户响应建模与定价决策综述[J].华东电力,2008,36(6).

[6刘观起,张建,刘瀚.基于用户对电价反应曲线的分时电价的研究[J].华北电力大学学报,2005,32(3).

[7]刘严,谭忠福,乞建勋.峰谷分时电价设计的优化模型[J].中国管理科学,2005,13(10).

[8]罗运虎,邢丽冬,王勤等.峰谷分时电价用户响应模型参数的最小二乘估计[J].华东电力,2009,37(1).

[9]谭忠富,王绵斌,乞建勋等.峰谷分时电价优化模型及其模糊求解方法[J].系统工程理论与实践,2008,9(9).

[10]丁伟,袁家海,胡兆光.基于用户价格响应和满意度的峰谷分时电价决策模型[J].电力系统自动化,2005,29(10).