利用有限元方法模拟微裂纹在强超声作用下的摩擦发热现象
陈赵江,张淑仪,郑 江,米小兵,郑 凯
(南京大学声学研究所近代声学实验室,南京 210093)
近年来,超声红外热像技术作为一种新型无损检测技术,已经引起国内外研究学者的广泛重视。由于超声红外热像技术是利用强超声激励下缺陷(裂纹)处的局部温升进行检测,因此缺陷(裂纹)发热机理的研究对于理解和改进超声红外热像技术有非常重要的作用。针对超声引起缺陷(裂纹)区域的局部发热机制,目前利用有限元方法已经进行了一些研究:如米小兵等给出了研究裂纹板中的振动分布以及裂纹局部发热的有限元算法步骤并进行了相应的数值模拟[1];Mian A等对超声红外热像技术中分层缺陷的摩擦发热现象进行了有限元仿真计算[2]。在上述研究中,超声激励被简化为作用在试样上的一个简谐位移函数,即有限元模型中并没有包含功率超声换能器系统。由于在超声红外热像技术中,功率超声换能器系统与试样之间的界面非线性效应对检测效果有非常重要的影响,因此上述假设导致了不准确的数值模拟结果。为进一步理解超声红外热像的检测机理,需建立更加合理的模型,做进一步的研究。
笔者利用显式瞬态动力学分析软件 LS-DYNA,对强超声脉冲激励下微裂纹的摩擦生热现象进行了有限元仿真。在有限元建模中,利用压电结构的热弹性类比方法(piezoelectricthermalanalogy)建立了基于显式算法的功率超声换能器模型。在有限元求解中,从三维弹性动力学方程出发,采用罚函数方法作为接触碰撞算法,并采用节点-单元法为接触搜索算法来实现对微裂纹在强超声激励过程中的接触、滑移及脱离等相互作用过程的模拟。采用显式-隐式混合积分算法进行结构-热耦合分析,对功率超声换能器激励下裂纹板的振动特性、裂纹面的动态接触过程以及裂纹处的温度分布进行了计算。
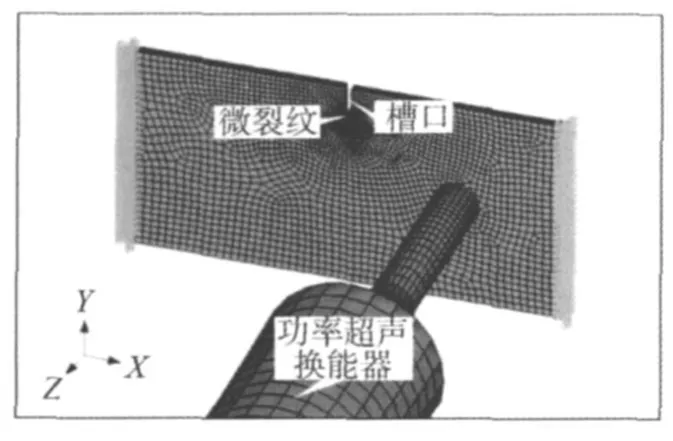
图1 有限元计算模型
1 有限元模型及建模分析
图1为强超声脉冲激励下裂纹摩擦发热现象模拟的有限元网格模型,包含功率超声换能器和铝合金裂纹板两个部分。铝合金裂纹板的尺寸为120mm×60mm×2.5mm,板的左右两个侧面固定(即约束其各个方向的平动和转动自由度)。该铝板上边缘有一长和宽分别为8和2mm的槽口,槽口下方有一长约4mm的微裂纹。在有限元模型中,功率超声换能器由压电陶瓷晶片、前后盖板和变幅杆等部分组成。笔者采用8节点六面体单元对换能器系统和铝合金板进行网格划分,其中板的厚度方向划分单元数为3个。为较为准确地模拟裂纹面在强超声脉冲激励下的动接触行为,对裂纹区域也进行了网格局部细划。
有限元方法已广泛应用于功率超声换能器系统设计和分析,但是目前的大多数显式有限元分析软件如LS-DYNA并不具备压电耦合场分析能力。因此,如何在显式有限元分析中模拟压电超声换能器的动力学特性是一个尚待解决的问题。由于显式有限元软件一般具有较为成熟的热-结构耦合分析能力,笔者采用压电-热弹本构方程的类比关系建立了基于显式算法的功率超声换能器有限元模型。
由于压电材料的应力-应变本构关系和热弹性本构关系非常相似,对于厚度伸缩型的压电作动器,可得到驱动电压和温度载荷之间的类比关系为[3]:

式中α为热膨胀系数向量;d为压电应变分量;Δθ为温度的改变量;t为压电薄片的厚度。式(1)和(2)表明,逆压电效应可以类比为热弹性效应;相应地,在有限元方程中,由于逆压电效应而产生的等效结点载荷也可类比为由于热弹性效应而产生的等效结点载荷。因此采用热弹性类比方法后可借助显式有限元软件分析热弹性效应的功能来分析逆压电效应并完成相应的瞬态动力学分析。通过相应的模态分析和谐响应分析,得到换能器的纵向振动固有频率为20kHz。而根据式(1)在压电片上施加不同幅值的交变温度载荷时,换能器变幅杆顶端具有不同的振动幅值,在文中空载条件下,变幅杆顶端的位移幅值为80μm。
变幅杆顶端与板面、以及微裂纹两个裂纹面之间的接触相互作用对板振动和裂纹摩擦生热现象具有非常重要的影响,因此需合理地模拟。在有限元模型中,变幅杆端面和板面分别设定为主面和从面,两个裂纹面也设为接触面(其中左裂纹面设为主面,右裂纹面设为从面)。此外,选定接触算法为罚函数方法并设定接触面的接触类型为面-面接触。由于裂纹表面粗糙,裂纹表面在相互滑动时会引起摩擦发热。根据热力学第一定律,易计算得摩擦发热等效热流密度q为:

式中ζ为摩擦能转化为热能的比例;v为滑移速度;τ为切应力。相应地,三维热传导瞬态方程可以写成如下形式:

式中 Φ为节点温度向量;L,H和Q分别为热容、热传导和热载荷矩阵;N为形函数。在求解上述热传导方程时,采用的是 Crank-Nicolson隐式积分方法。由于通常裂纹附近区域温度比较低,而所关心的问题持续时间又很短(仅为几百毫秒),所以在以上计算过程中,裂纹附近区域发生的空气对流与热辐射散热被忽略。此外,为简单起见,设定裂纹面的动摩擦系数等于静摩擦系数,且为0.3。
2 计算结果分析与讨论
从超声红外热像试验可知,当换能器系统的预紧力相对较小时,变幅杆与待检试样之间存在较强的界面非线性效应并导致试样产生声混沌振动现象[4]。图2为换能器系统的预紧力载荷等于150N时,铝合金裂纹板的振动情况。从图2(a)中的插图可知,板振动波形非常复杂,可认为是一种准周期振动,而图2(a)中板的振动频谱成分非常丰富,包含幅值较高的次谐波和超次谐波成分,即产生了声混沌振动现象。图2(b)为变幅杆与板面之间的接触力波形展开图,接触力形态表现为一系列力脉冲的形式,并且不同的力脉冲具有不同的幅值。从图2(b)也可看出,板的声混沌振动是由于变幅杆与板面之间的间歇性接触引起。


根据图2所示的板的振动条件,计算得到如图3所示的裂纹面运动状态。从图3(a)中的裂纹面接触力波形可以看到,在强超声脉冲激励下,裂纹面之间存在一定的接触压力的作用,其值约为几十牛顿。此外,裂纹面接触力波形包含丰富的频谱成分,如阶数较高的次谐波和超次谐波成分。裂纹接触力中丰富的频谱成分主要是由于裂纹板X方向的振动中包含幅值较强的超谐波和次谐波成分,其根源在于变幅杆与板之间的接触非线性。图3(b)给出了左右裂纹面节点Z方向(垂直于板面方向)的相对速度波形(插图)和频谱,其中节点距离裂纹尖端的距离为2.0mm。从图中的插图可知,左右裂纹面具有一定的相对速度(即裂纹面出现相对运动),并且不同位置节点的相对速度不同。此外,裂纹面相对速度波形频谱也具有丰富的超谐波和超次谐波成分。由于裂纹面之间存在一定的接触压力,并且裂纹面之间存在相对运动,因此在裂纹处会产生摩擦生热现象。
图4给出了上述条件下裂纹附近区域温度分布随超声激励时间的变化情况,其中黑色区域为槽口,中间黑色线条为裂纹。图4中温度灰度图的温度幅值范围为27.0~27.7℃,其中裂纹板的初始温度为27.0℃。从图可知,由于具有一定的接触压力以及相对速度,裂纹面出现了明显的温升现象。随着超声激励时间增加,裂纹处摩擦生热产生的热能量增多,并且热量逐渐向四周扩散,从而形成一个亮斑,并且亮斑的面积逐渐扩大。从图中也可看到,亮斑的亮度较强,即温升的幅值较大。在t=120 ms时刻,裂纹面及其附近的最大温升超过0.70℃。

图4 强超声脉冲激励下裂纹附近区域的温度分布
图5为裂纹面上两个不同节点温度随时间变化曲线,其中节点位置分别位于裂纹尖端和裂纹中部。从图中的曲线可看出,当超声激励开始后,裂纹面上节点的温度迅速升高。此外,由于热扩散的原因,温升曲线在一段时间后趋于平缓。由于裂纹中部节点具有相对较大的接触压力和相对速度,生成的热能量比裂纹尖端节点多,其温升曲线具有较大的斜率。在t=120 ms时刻,裂纹中部节点的温升约为0.78℃,而裂纹尖端节点的温升约为0.33℃。从图中可看出,声混沌条件下裂纹处的温升曲线不光滑,包含一定的波动。温升曲线产生波动的原因是由于裂纹接触力的间歇性接触周期较长(在接触力脉冲间隔内,温度可能轻微下降),再加上复杂的裂纹接触力和相对速度波形共同作用引起。

图5 强超声脉冲激励下裂纹面节点温度随时间变化曲线
3 结论
采用有限元方法研究了超声红外热像技术的缺陷检测机理,对功率超声换能器激励下裂纹面的动接触行为和摩擦生热现象进行了有限元仿真并得到了以下结论:
(1)由于功率超声换能器变幅杆与待检金属板之间存在界面非线性效应,导致裂纹面接触力以及相对速度波形中包含丰富的频谱成分。
(2)在超声激励过程中,两个裂纹面之间将产生相对运动,并出现接触、滑移和分离等现象。由于裂纹面不光滑,因而会出现摩擦生热现象。在强超声脉冲激励下,两个裂纹面运动具有不同的幅值和相位,会出现相对运动。此外,裂纹面之间存在一定的接触压力的作用,接触压力表现为力脉冲的形式。由于裂纹面产生相对运动并有一定的接触压力,因而产生摩擦生热现象。
(3)通常微裂纹在超声激励过程中的动接触行为较为复杂,因此微裂纹表面温升曲线包含一定的波动。此外,由于热扩散的原因,裂纹面的温度不能无限上升,在一定时间后温升曲线将趋于平缓。
(4)试验计算结果可以定量解释在超声红外热像技术中观察到的现象。
[1]米小兵,张淑仪.超声波引起固体微裂纹局部发热的理论计算[J].自然科学进展,2004(14):628-634.
[2]Mian A,Newaz G,Han X Y,et al.Response of subsurface fatigue damage under sonic load-a computational study[J].Composites Science and Technology,2004(64):1115-1122.
[3]Cote F,Masson P,Mrad N,et al.Dynamic and static modelling of piezoelectric composite structures using a thermal analogy with MSC/NASTRAN[J].Composite Structures,2004(65):471-484.
[4]Han X,Li W,Zeng Z,et al.Acoustic chaos and sonic infrared imaging[J].Applied Physics Letters,2002(81):3188-3190.

