重力坝坝基抗滑稳定计算方法

郭天明

(山西省水利水电勘测设计研究院,山西 太原 030024)

重力坝坝基抗滑稳定计算方法

郭天明

(山西省水利水电勘测设计研究院,山西 太原 030024)

为研究重力坝坝基抗滑稳定性,以含软弱夹层复杂地质条件的重力坝为研究对象进行分析。从刚体极限平衡法出发,对各参数的敏感性进行分析评价,用刚体极限平衡法和ANSYS分析软件分别进行抗滑稳定计算,并进行结果对比。有限单元法与刚体极限平衡法得出的坝基深层抗滑稳定安全系数较为接近。有限单元法能分析各种复杂形状,比刚体极限平衡法更接近于真实状态。

抗滑稳定;极限平衡法;ANSYS;对比分析

0 前 言

在实际工程中,重力坝坝址的地质结构极为复杂,坝基内往往存在不利的结构面,重力坝的深层抗滑稳定也随之变得更加复杂。因此抗滑稳定一直是重力坝设计中的一项重要内容。

现在对于坝基深层抗滑稳定的分析方法中,刚体极限平衡法仍然是主要方法[1],这种方法简单实用,但是刚体极限平衡法仅考虑了岩体的强度特性,未将地基作为变形体,不能给出地基内应力和变形的分布情况,而且在求解时须采用许多假定,忽略了一些复杂的地质条件,从而导致了一些计算结果不够准确。近年来,随着计算机的发展,有限单元法己经发展得非常成熟和完善。有限单元法可以较大范围考虑地质构造的复杂性,能较精确地分析坝体和坝基的应力和变形,对极限平衡方法有很大改进和补充。

本文对地质条件较为复杂的重力坝工程挡水坝段进行了分析探讨,从传统的刚体极限平衡法出发,对各参数的敏感性进行了分析评价,得出坝基深层抗滑稳定安全系数,并与运用ANSYS分析软件计算的结果进行了对比分析。

1 工程实例

1.1 工程概况

某重力坝坝顶高程683.8 m,最大坝高49.8 m,坝顶长240 m,坝顶宽6 m,坝底宽47.42 m上游水深48.2 m,下游水深6.75 m。大坝左右坝肩各有一条断层,坝基存在两层软弱结构面,其滑动示意图见图1。

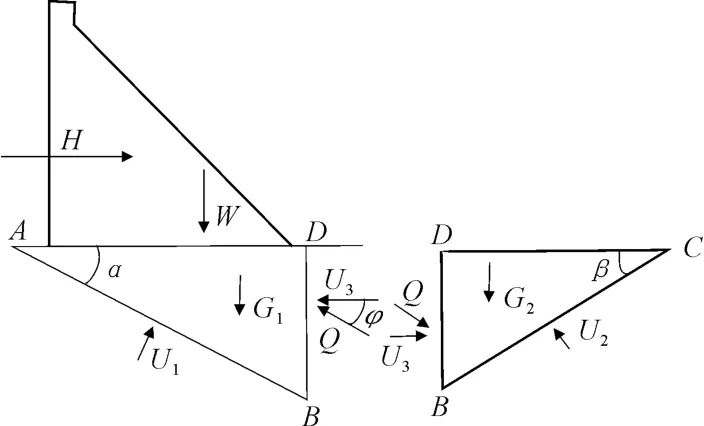
图1 双斜面滑动示意图

1.2 模型影响因子敏感性分析

考虑ABD块的稳定,则有:

式中:K′1、K′2为按抗剪断强度计算的抗滑稳定安全系数;W为作用于坝体上全部荷载(不包括扬压力,下同)的垂直分值(kN);H为作用于坝体上全部荷载的水平分值(kN);G1、G2分别为岩体ABD、BC D重量的垂直作用力(kN);f′1、f′2分别为AB软弱夹层面、BC剪切破裂面的抗剪断摩擦系数;c′1、c′2分别为AB软弱夹层面、BC剪切破裂面的抗剪断凝聚力(kPa);A1、A2分别为AB、BC面的面积(m2);α、β 分别为软弱夹层面AB、剪切破裂面BC面与水平面的夹角;U1、U2、U3分别为AB、BC、BD面上的扬压力(kN);Q、φ分别为BD面上的作用力及其与水平面的夹角。夹角φ值需经论证后选用,从偏于安全考虑 φ可取0。

通过式(1)、式(2)及K′1=K′2=K′,可求解抗滑稳定安全系数K′值。

当坝基中的软弱夹层成为坝体深层抗滑稳定的控制滑动面时,则软弱夹层的物理力学性质对坝体的抗滑稳定安全至关重要,而其中抗剪断摩擦系数f′和抗剪断凝聚力c′最为重要[2]。计算中取抗剪断摩擦系数f′在0.25～0.47之间每增加0.02计算抗滑稳定安全系数,软弱夹层面的抗剪断凝聚力c′在2 kPa～57 kPa之间每增加5 kPa计算抗滑稳定安全系数。得出抗滑稳定安全系数随软弱夹层面抗剪断摩擦系数f′和抗剪断凝聚力c′的变化趋势见图2和图3。

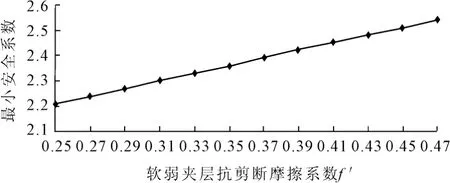
图2 坝基深层抗滑稳定安全系数k随软弱夹层面抗剪断指标 f′的变化趋势

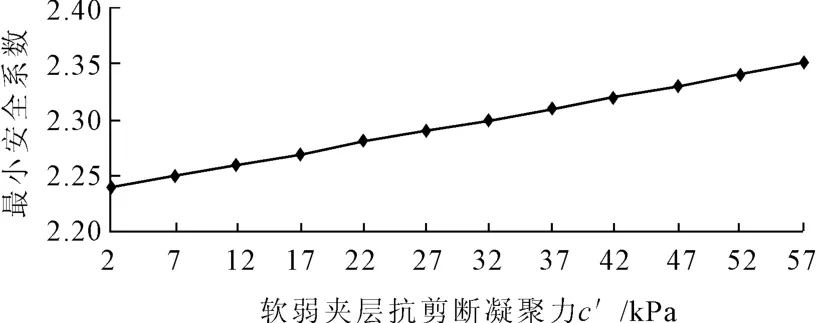
图3 坝基深层抗滑稳定安全系数k随软弱夹层面抗剪断指标c′的变化趋势

由图2和图3可知:软弱夹层面上的抗剪断摩擦系数f′在0.25～0.47之间变化时,坝基深层抗滑稳定安全系数随抗剪断摩擦系数的增加而增大。抗剪断摩擦系数每增加0.02,安全系数增加0.03左右。软弱夹层面的抗剪断凝聚力c′在2 kPa～57 kPa之间变化时,坝基深层抗滑稳定安全系数随抗剪断凝聚力的增加略有增大。抗剪断凝聚力每增加10 kPa时,安全系数增加0.02。

1.3 刚体极限平衡法计算抗滑安全系数

计算时选取地势较低的6#坝段(泄洪排沙底孔坝段)作为典型坝段,分两种工况进行研究,第一种是正常蓄水位工况,第二种是校核洪水位工况。由于6#坝段的上层软弱夹层埋深较浅,为了改善稳定性,对上层软弱夹层进行了开挖置换的工程处理,只计算下层软弱夹层的抗滑稳定安全系数。根据刚体极限平衡法计算坝段整体的深层抗滑稳定,按图4双斜面深层抗滑稳定计算简图,根据地质资料选取软弱夹层面上的力学指标f′1为0.25,c′1为5 kPa,剪切破裂面上的岩体力学指标第一层f′2为 0.750,c′2为 700 kPa;第二层f′2为0.750,c′2为1 200 kPa。软弱夹层与水平面的夹角取为7.5°。剪切破裂面起始点B的水平投影点D由坝趾正下方向下游移动变化,剪切破裂面滑出点C根据β值变化可向下游移动变化。以AD,β为变量,AD从AE～(AE+30m)之间变化(AE为坝底宽度),计算步长为1m;β在1°～89°之间变化,计算步长为2°。计算的出最危险滑动面参数见表1。

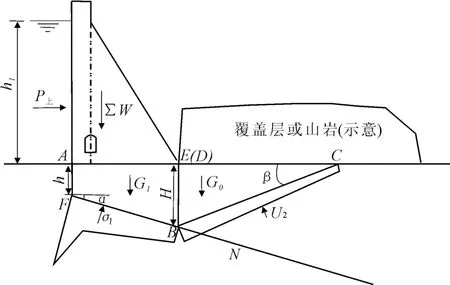
图4 软弱夹层双斜面深层抗滑稳定计算简图

表1 深层抗滑稳定计算结果

1.4 有限元法计算抗滑安全系数

在考虑材料非线性及各种荷载对坝段进行有限元计算时,运用大型有限元计算程序ANSYS进行三维非线性有限元分析计算[3]。建立模型是考虑了坝体周围复杂的地形、左右坝肩的断层以及地基内的两条软弱夹层带。整体有限元计算模型如图5所示,6#坝段模型如图6所示。

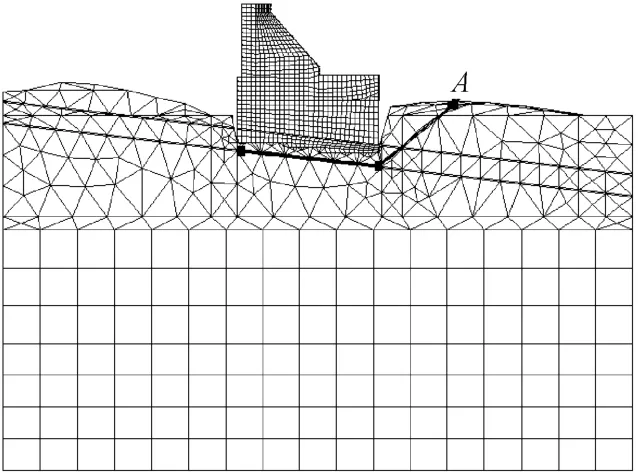
图5 重力坝整体三维有限元模型

根据有限元结果计算稳定安全系数时,用下列步骤计算:首先根据地质状况和刚体极限平衡法确定可能滑动面(见图5中的路径A)。然后根据有限元结果计算出沿可能滑动面的正应力和剪应力,再计算抗滑稳定安全系数。

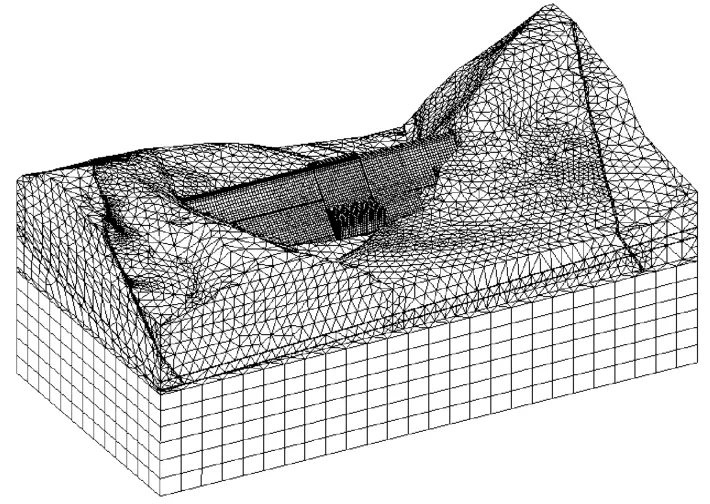
图6 6#坝段有限元模型

在重力坝的深层滑动中,当可能滑动面不再是一个平直的滑动面,而是由若干个滑动面组成的折面时,由于没有单一的滑动方向,无法简单将滑动力和抗滑力投影到一个滑动面,因此当采用有限元法计算时,可以将滑动力和抗滑力分别投影到各自平直滑动面上,再分别叠加,根据规范规定,在大坝基础内存在可能引起滑动的软弱面时,必须用下式分别计算可能滑动面的整体和局部抗剪断安全系数[4]:

整体安全系数:

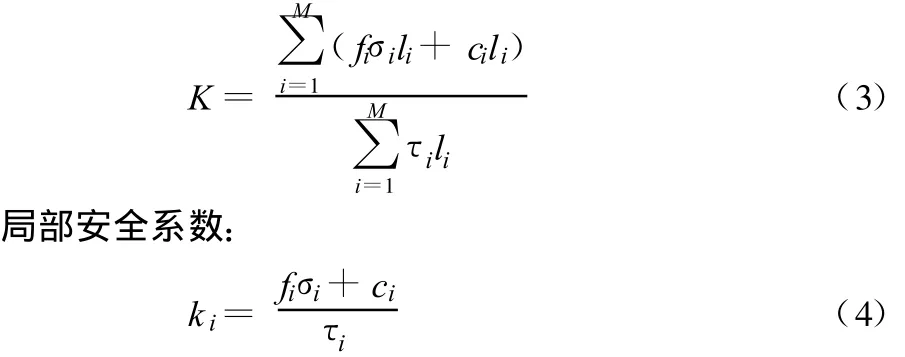
式中:M为构成滑移面的折面总数;σi、τi为折面i上作用的法向有效应力和切向应力;fi、ci、li分别为折面i的摩擦系数、凝聚力和线段长度。

有限元结果与刚体极限平衡法计算的整体安全系数比较见表2。

由表2计算结果可以看出,正常蓄水位的基本荷载组合坝基中的软弱夹层的抗滑安全系数均在3.0以上,校核洪水位的特殊荷载组合坝基中的软弱夹层的抗滑安全系数均在2.5以上,因此可以判定坝体是稳定的。

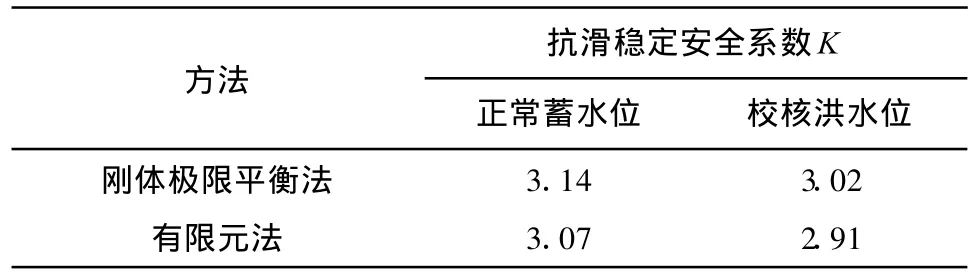
表2 软弱夹层的抗滑安全系数

2 结 论

(1)刚体极限平衡法算法简单、工程经验丰富、有与之配套的稳定评价标准。由此,对重力坝抗滑稳定的研究,仍是以刚体极限平衡法为主,并以有限元法等加以复核。

(2)有限单元法能分析各种复杂形状、多种材料组成的地基条件,计算模型不仅满足力的平衡方程,而且满足土体的应力应变关系,比刚体极限平衡法更接近于真实状态,具有很好的适用性。

[1]林继镛.水工建筑物[M].北京:中国水利水电出版社,2006:44-53.

[2]彭一江,黎保琨.复杂地基重力坝深层抗滑稳定非线性有限元分析[J].中国安全科学学报,2005,15(3):82-86.

[3]李围.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2005:76-120.

[4]张国新,金峰.重力坝抗滑稳定分析中DDA与有限元方法的比较[J].水利发电学报,2004,23(1):11-14.

Calculation Methods for Stability Against Sliding of Gravity Dam's Base

GUO Tian-ming
(Shanxi Investigation and Design Institute of Water Conservancy and Hydropower,Taiyuan,Shanxi030024,China)

In order to study the stability against sliding of gravity dam's base,the gravity dam with the weak interlayers and complex geologic conditions is adopted as an investigated subject.The limit equilibrium method of rigid body and ANSYS software are applied to analyze and appraise the sensitivity of various parameters,make calculation for the slability against sliding and make comparison for the calculation results.The results show that compared with the limit equilibriummethod of rigid body,the finite element method is further in agreement with the actual conditions as it could be used to analyze the various complex forms.

stability against sliding;limit equilibrium method;ANSYS;comparative analysis

TV642.3

A

1672—1144(2010)02—0121—02

2010-01-15

2010-01-21

郭天明(1979─),男(汉族),山西右玉人,工程师,主要从事水利水电工程设计。