平原地区农村供水工程的优化布局

余轶鹏,陶月赞,余晓庆

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

平原地区农村供水工程的优化布局

余轶鹏,陶月赞,余晓庆

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

目前农村饮水工程因多方面因素影响,普遍存在着工程布局不合理现象。以安徽蒙城县为研究对象,从农村水厂的投资费用考虑,综合两方面因素对农村供水工程的布局进行优化,首先以供水经济距离为依据确定其供水范围,再在供水范围内建立以工程投资和运行费用最小为目标的线性规划模型。提出了在经济供水半径范围内的优化布局方案,即在乐土镇建水厂总费用最小。水厂的选址与用水量和供水距离有着密切的关系,在供水范围的中心区域建厂并不一定经济。

农村供水;经济距离;线性规划;水厂布局

目前农村饮水安全工程正积极开展建设,由于农村地区居住分散,点多面广,以及水源条件和地利条件等多种因素影响,导致大部分供水工程供水规模不合理,规模普遍较小,工程布局不合理,重复建设现象严重。随着城乡统筹步伐的加快和社会主义新农村建设的全面推进,未来相当长一段时期内,农村供水方面的工作任务和政府投资需求将面临挑战。因此对农村供水工程的研究有着重要的现实意义。

本文以蒙城县为研究对象从农村水厂的投资费用角度分两阶段对农村水厂的布局进行优化,第一阶段优化以供水经济距离为依据在供水区域确定其供水规模,第二阶段建立水厂选址优化模型在供水范围内对厂址进行优化选择。

1 水厂布局初级优化—供水范围的确定

供水范围的确定与当地地形、水资源条件、居民点的分布有关。随着我国农村经济的发展和广大农民生活水平的提高,发展集中供水模式是农村供水工程建设的方向[1～3]。随着水厂生产规模的扩大,按照其产生的规模经济性质可分为规模内经济和规模内不经济两类。在规模内经济范围内,随着生产规模的扩大,单位制水成本下降;规模不经济范围内,制水规模达到一定点时,制水能力超出现有设备能力限制,若进一步扩大生产,势必增加设备等资金投入,边际制水成本大幅度提高,单位制水成本上升。因此,在一定范围内单位制水成本会随着生产规模的变化呈现先降后升的U形函数形式[4,5],故确定供水规模对水厂的可持续运行起着关键作用。

针对新建农村水厂,构造简单的数学模型,以蒙城县及周边县、市已建的农村供水工程资料为基础,建立供水量、水价和供水半径之间的函数关系,通过分析这些函数关系,讨论供水半径对供水量、水价以及供水工程经济性的影响,提出供水经济半径的概念为农村供水规模的选择、供水范围的取舍提供了数学依据,使得现阶段建设的集中供水工程能够选用合理的供水规模、确定合适的供水范围。

1.1 供水工程费用分析

农村供水工程投资主要包括水厂投资(包括水源地建设)、供水管网一次性基建投资、运行管理费用[6]。

1.1.1 水厂建设费用

在假定区域内人口平均分布的情况下,需水量、供水半径、区域人口密度之间存在以下函数关系:

式中:Q为需水量(L/s);r为供水半径(km);P为人口密度(人/km2);q为人均综合用水量(L/s◦人)。

在一定区域内,可通过已建供水工程资料,通过回归分析,建立该区域水厂建设费用W与制水量Q之间相应的函数关系:

式中:W为水厂建设费用(万元);Q为制水量(本文中假设制水量等同需水量)(L/s)。

参照蒙城及邻近几个县市、地区的已建供水工程资料实际数据和计算数据,综合比较得出不同制水规模下水厂工程建设投资,绘制相关曲线如图1所示。

图1 水厂制水规模与工程建设投资关系

由图1可知,蒙城县范围内,水厂建设费用W与制水量Q之间相应的函数关系为:

式中:W的单位为万元;Q的单位为103m3/d。

1.1.2 管网基建投资

由于农村供水工程用户点多面广,采用的供水管网布置形式多种多样,无法准确估计管网基建费用与相关参数的关系,可依据现有的供水管网建设资料绘制点状分布图(蒙城县农村供水工程管网建设投资与供水半径关系如图2),通过回归分析,从而得出该地区管网基建投资和供水半径间相对粗糙的函数关系:

式中:C为管网基建投资(元);其余符号意义同式(1)。

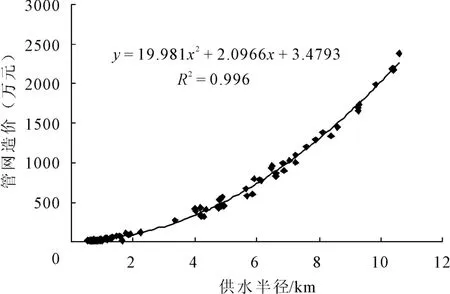
图2 供水半径与管网基建投资关系

为了提高准确性,在进行回归分析时,需考虑到管网实际建设与投资情况,适当的调节函数关系式各参数的选取:供水半径较小时,入村、入户等小管径管道建设资金占有管网总投资相当大比例,而输水主管道建设资金部分比例较小;随着供水半径的增大,输水主管道建设投资占有的比例将会越来越大。

1.1.3 运行管理费用

每年的运行管理费用包括动力费M1和折旧大修理费M2[7],分别等于:

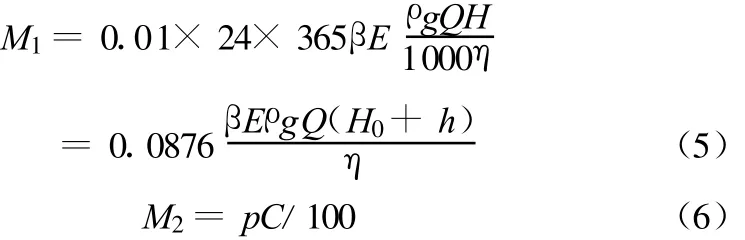
式中:M1为动力费(元);M2为折旧大修费(元);β为供水能量变化系数;E为电费(分/kWh);ρ为水的密度,ρ=1 kg/L;g为重力加速度,g=9.81 m/s2;p为每年扣除的折旧和大修费用,以管网造价的%计;H为泵站扬程,对于长距离输水,可不考虑局部水头损失(m);H0为水泵静扬程,与水源井动水位相对应(m);h为管网水头损失(m);η为泵站效率;其余各式意义同式(1)～(4)。

一定区域内,在各经济参数和供水半径确定的情况下,式(5)中只有管网水头损失h未知,农村供水管网布置形式多种多样,无法准确估计管网水头损失和管网规模关系,同样可根据现有的管网运行资料绘制相关点状图(蒙城县农村供水工程供水半径与管网水头损失关系如图3),通过回归分析,建立该地区管网水头损失与供水半径之间简单的函数关系:

式中:h为管网水头损失(m);r为供水半径(km)。

图3 蒙城供水半径与管网水头损失关系

1.2 模型构造

在供水半径确定的情况下,供水辐射范围内每年的水费收入R(已扣除制水成本)为:

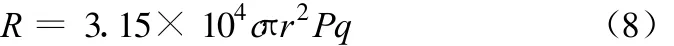
式中:R为水费收入(元);c为水价;其余符号意义同式(1)。

考虑供水设施的建设、运行、管理等因素,建立供水经济半径估算数学模型:

利用静态投资分析方法进行分析,则工程服务期末净现值A为:

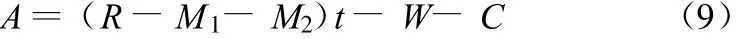
式中:A为工程期末净现值(元)。

根据蒙城县已建供水工程资料,可确定各参数取值如:

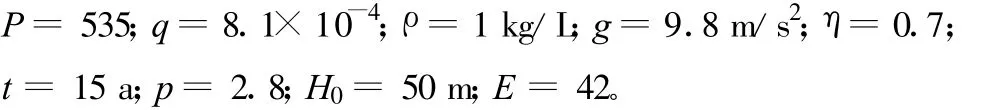
将上述参数及式(1)～(8)代入式(9),则可得到工程期末净现值A和未知变量r之间的函数为(相关关系如图4所示):

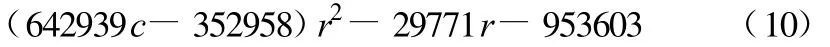
在水价一定的情况下,对于一次性建成的供水工程,可计算出不同的供水半径下的工程服务期末净现值,若使得此净现值大于零,便认为采用该供水半径的供水方案是经济可行的,把满足此条件的供水半径称为供水经济半径。

图4 蒙城县供水半径与净现值关系

由图4可知:①水价低时,可采用的经济供水半径范围较小,获得的工程期末净现值较低;水价高时,可采用的经济供水半径范围较广,相应的工程期末净现值较高;②在获得同样净现值的情况下,供水半径较大的,其相应的供水价格相对较小,体现了规模经济的优势;③供水半径趋于一定范围内才能体现出来工程的经济性;反之,供水半径过大或过小都会导致工程处于不经济运行范围。

2 水厂布局二级优化—选址问题

由供水经济距离的研究可对区域水厂布局进行初步规划,确定了其供水规模。但对供水区域内水厂的选址问题需要进一步研究。

水厂布局优化能充分发挥水资源、能源的作用,节省投资和运行费用,有很大的经济意义和社会意义。水源和用户的位置、选址地的高程、输配水设施运行成本影响着水厂布局,而年运行费用包括折旧、修理维护、动力费等,反映上述影响因子,所以,水厂布局优化问题转化为输配水设施及管网运行费用最小的问题。根据运行费用最小这一思路,建立数学模型,求解得出结论。

2.1 模型构造

平原地区水厂的厂址选择在满足水源、水量、水质的前提下,以供水工程经济投资和运行费用最小为目标建立厂址优化的线性规划[8]模型。

设供水区域有m个水源地,表示为A1,A2,…,Am,供水量为a1,a2,…,am单位m3/d;用水区域有n个,表示为B1,B2,…,Bn,其需水量分别为:b1,b2,…,bn,单位为m3/d。

从水源Ai到用水区Bj的供水量为Qij(m3/d),单位距离单位供水成本(包括基建费用)为k〔元/(km◦m3)〕,从水源Ai到用水区Bj的距离为Lij(此距离为供水管道实际铺设距离非直线距离),单位km。

2.2 模型的应用

蒙城地区目前地表水污染较为严重,第四系地层赋存松散孔隙水,第四系的厚度由西、西北部大于700 m渐变至北部、东南部小于100 m;涡河以北出露的零星山丘为寒武系灰岩和泥灰岩,该区段赋存有裂隙岩溶水,因此该地区供水水源以地下水为主。

对模型进行简化,由于水源地为地下水,为方便管理水厂一般建在村镇附近可近似看作在用水区Bj处,即Ai到Bj的距离Lij为零(i=j)。水源统一进入水厂进行净化配送,即由水源所在地用水区Bi往其它用水区Bj供水。模型可简化为,

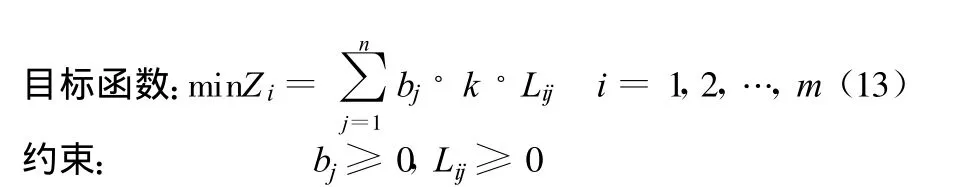
农村村落布局点多面广在初步规划中以镇为中心作为主要用水点,在二级优化中为了准确确定水厂位置,需要对用水区进一步细化。对三义、乐土中心镇周边村落作为用水区域,见图5,依次标注为B1,B2,…,B11,根据蒙城县农村居民生活水平,取居民综合用水量为100 L/d,则其需水量表示为b1,b2,…,b11;水厂厂址选择在用水区附近,则水厂与用水区的距离Lij为各用水区的供水距离,见表1。

图5 供水区域村镇位置图

min(Zi/k)=Z4/k=21400,也即最小费用minZ为21400k元。因此厂址的选择在B4总的费用最小,适合在B4处即乐土镇建水厂。

由结论可看出水厂的选址与用水量和供水距离有着密切的关系,在供水范围的中心区域建厂并不一定经济。

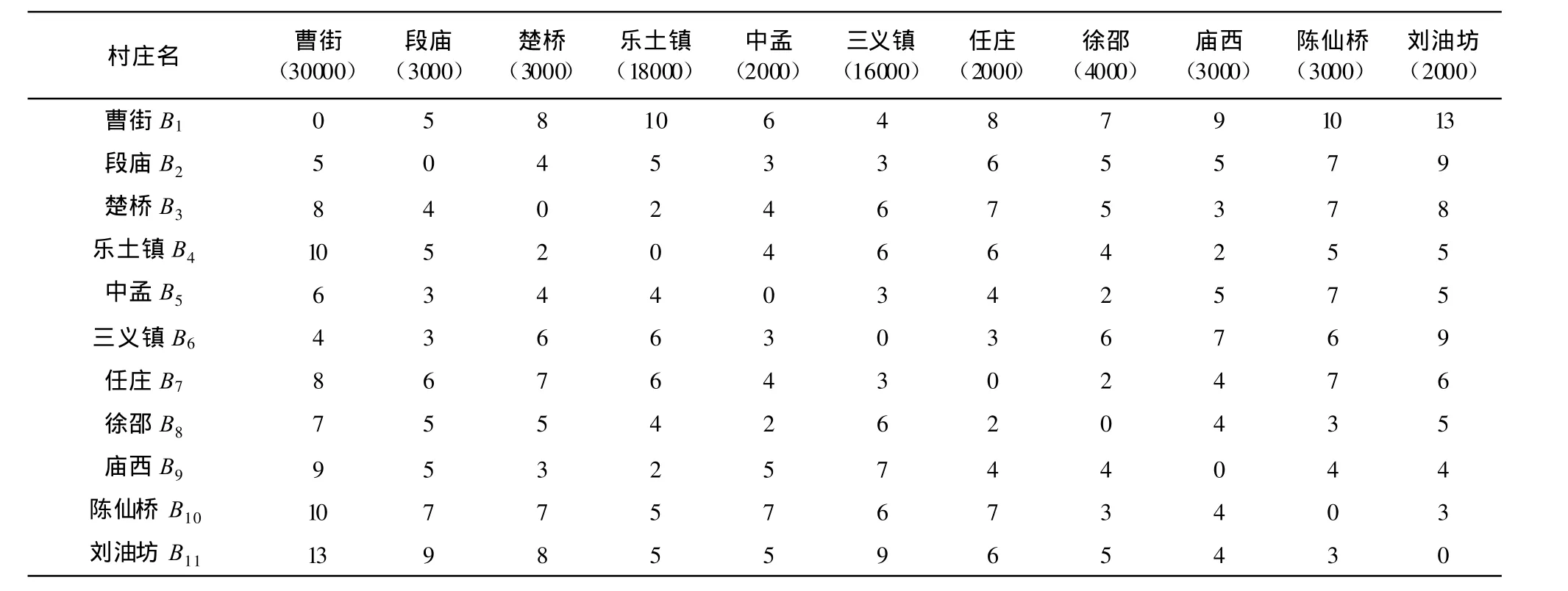
表1 用水区之间距离(km)

3 结 论

(1)利用供水规模与供水半径、工程投资、制水成本的关系,为供水规模的研究提供理论依据。合理选择供水规模对工程的经济性和可持续运行起着至关重要的作用。

(2)运用线性规划求解方法对供水范围内的水厂厂址进行优化选择,对厂址的选择提供了决策依据,对供水工程的高效运行和对工程投资的有效利用有着重要的参考意义。

(3)本文的研究对象是蒙城平原地区,而对于山区、丘岭等地形起伏较大、水源不稳定且用户较分散地区,文中的方法有一定的局限性,如何解决这类地区的供水规划问题有待进一步的研究。文中单位供水成本k,需要大量工程资料进行参数拟合,需随着工程进行进一步修正。

[1]刘学功,刘文朝,崔招女.农村供水工程发展模式及工程规划设计应注意的问题[J].中国水利,2005,(17):59-61.

[2]杨继富.农村饮水安全科技支撑现状及建议[J].中国水利,2007,(17):16-18.

[3]郭孔文,胡 孟.农村供水工程发展模式探讨[J].中国水利,2006,(19):38-40.

[4]任鸣鸣,杨超,何 波.生产成本规模递减的工厂选址和规模决策[J].工业工程与管理,2007,12(6):98-103.

[5]方红远,王银堂.边际成本分析在水资源开发利用决策中的应用[J].水科学进展,2004,15(2):243-248.

[6]严煦世,范瑾初.给水工程[M].北京:中国建筑工业出版社,1999.

[7]白丹.树状给水管网的优化[J].水利学报,1996,(11):52-56.

[8]《运筹学》教材编写组.运筹学(第三版)[M].北京:清华大学出版社,2005.

Optimal Layout on Rural Water Supply in Plain Area

YU Yi-peng,TAO Yue-zan,YU Xiao-qing
(College of Civil and Hydraulic Engineering,Hefei Polytechnical University,Hefei,Anhui230009,China)

At present,there exist the unreasonable practices in the layout of rural water supply engineering.Taking Mengcheng County as a research object,the two-phase optimizations on the layout of rural water supply engineerings are analyzed here from the point of the investing cost of rural waterworks.The first phase optimization focuses on the determination of water supply area and numbers of waterworks on the basis of economic distance,while in the second phase,the optimization for layout of waterworks is made by building a linear programming model of minimum water supply cost within the water supply area.

rural water supply;economical distance;linear programming;waterworks layout

TU991

A

1672—1144(2010)02—0106—04

2009-09-25

2010-01-14

余轶鹏(1982—),男(汉族),安徽安庆人,硕士研究生,主要研究方向为给排水工程与技术。